2.3 Численное решение определенных задач

Пример 1. Пользуясь явной схемой, найти приближенное решение начально-краевой задачи вида:

,

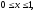(начальное условие)

, (краевое условие на левой границе)

, (краевое условие на правой границе).

Решение.

Сравнивая с общей постановкой задачи, получаем .

Зададим шаг по пространству: h=0,1 , следовательно, Выберем шаг по времени из условия обеспечения устойчивости и минимизации ошибок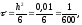поэтомуТаким образом, получаем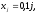

Вычислим значения решения на нулевом слое:

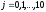(N=10).

Краевые условия на левой и правой границах записываются в виде:

(K=6).

2, 3. Поскольку решение на следующих слоях при k=0,1,…,5 находится по формуле

j=1,…,9,

и занесено в таблицу

k j	0	1	2	3	4	5	6	7	8	9	10
0	0	0.360	0.640	0.840	0.960	1.000	0.960	0.840	0.640	0.360	0
1	0	0.347	0.627	0.827	0.947	0.987	0.947	0.827	0.627	0.347	0
2	0	0.336	0.613	0.813	0.933	0.973	0.933	0.813	0.613	0.336	0
3	0	0.326	0.600	0.800	0.920	0.960	0.920	0.800	0.600	0.326	0
4	0	0.317	0.588	0.787	0.907	0.947	0.907	0.787	0.588	0.317	0
5	0	0.309	0.576	0.774	0.894	0.934	0.894	0.774	0.576	0.309	0
6	0	0.302	0.564	0.761	0.881	0.921	0.881	0.761	0.564	0.302	0

Полученное решение на каждом из временных слоев является симметричным.

Решена задача параболического типа методом сеток. При решении использовали явную схему, вычисления обработаны на MathCad и выведены в виде кривых (Приложение 1).

Пример 2. Пользуясь явной схемой, найти приближенное решение начально-краевой задачи вида:

,

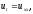
(начальное условие)

, (краевое условие на левой границе)

, (краевое условие на правой границе).

Решение.

Сравнивая с общей постановкой задачи, получаем .

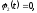
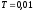Зададим шаг по пространству: h=0,1 , следовательно, Выберем шаг по времени из условия обеспечения устойчивости и минимизации ошибокпоэтомуТаким образом, получаем

Вычислим значения решения на нулевом слое:

(N=10).

Краевые условия на левой и правой границах записываются в виде:

(K=6).

2, 3. Поскольку 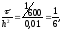решение на следующих слоях при k=0,1,…,5 находится по формуле

j=1,…,9,

и занесено в таблицу

k j	0	1	2	3	4	5	6	7	8	9	10
0	0	0.005	0.020	0.045	0.08	0.125	0.180	0.245	0.320	0.405	0.500
1	0.002	0.007	0.022	0.047	0.082	0.127	0.182	0.247	0.322	0.407	0.502
2	0.003	0.008	0.023	0.048	0.083	0.128	0.183	0.248	0.323	0.408	0.503
3	0.005	0.010	0.025	0.050	0.085	0.130	0.185	0.250	0.325	0.410	0.505
4	0.007	0.012	0.027	0.052	0.087	0.132	0.187	0.251	0.327	0.412	0.506
5	0.008	0.013	0.028	0.053	0.088	0.133	0.188	0.253	0.328	0.413	0.508
6	0.010	0.015	0.030	0.055	0.090	0.135	0.190	0.255	0.330	0.415	0.510

Решена задача параболического типа методом сеток. При решении использовали явную схему, вычисления обработаны на MathCad и выведены в виде кривых (Приложение 2).

Пример 3.

Дана система линейных алгебраических уравнений с трехдиагональной матрицей А (n=4):

5x1+3x2=8,

3x1+6x2+x3=10,

x2+4x3-2x4 =3,

x3-3x4 =-2

.

Имеем рекуррентные соотношения для (2.68). Определение прогоночных коэффициентов по формулам (2.68) соответствует прямому ходу метода прогонки.

Обратный ход метода начинается с вычисления . Для этого используется последнее уравнение, коэффициенты которого определены в прямом ходе, и последнее уравнение исходной системы определяется известной формулой (2.69).

Результаты занесены в исходную таблицу.

j	aj	bj	cj	dj	Aj	Bj	xj
1	0	-5	3	8	-3/5	8/5	1
2	3	-6	1	10	-5/21	26/21	1
3	1	-4	-2	3	42/79	37/79	1
4	1	3	0	-2	-	1	1

Прямой ход Обратный

ход

Решена система методом матричной прогонки на языке Turbo Pascal 6.0. (Приложение 3).

Заключение

Численное решение прикладных задач всегда интересовало математиков, так как краевые задачи которые возникают в различных областях математической физики, посвящены теплопроводности, диффузии, движению жидкостей, акустике, электромагнетизму, волновой механике, переносу лучистой энергии, упругим колебаниям решаются аналитически в определенных задачах.

В настоящее время с быстрым развитием вычислительной техники позволяет многие задачи быстро решить численными методами, даже если они решаются аналитическим способом.

В дипломной работе рассмотрены конечно-разностные методы решения задач для дифференциальных уравнений в частных производных параболического типа, такие как неявно-явная конечно-разностная схема с весами; схема Кранка-Николсона; метод дробных шагов Н.Н. Яненко; метод переменных направлений с экстраполяцией В.Ф. Формалева; однородные и консервативные конечно-разностные схемы для задач теплопроводности с граничными условиями, содержащими производные.

Дипломная работа состоит из двух параграфов:

первый параграф посвящен ключевым определениям дифференциальных уравнений в частных производных, приведению уравнений второго порядка в частности параболического типа к каноническому виду, а также постановке задач для уравнений параболического типа;

второй параграф состоит из трех подразделов. Первый подраздел содержит основные определения и конечно-разностные схемы для дифференциальных уравнений параболического типа, здесь подробно описываются понятия аппроксимации, порядка аппроксимации, сходимости, порядка сходимости, устойчивости, а также описание различных методов исследования устойчивости. Во втором подразделе проанализированы неявно-явные конечно-разностные схемы, как следствие двухсторонних методов, с исследованием аппроксимации и устойчивости для схем типа Кранка-Николсона. При численном решении многомерных задач математической физики исключительно важным является вопрос об экономичности используемых методов. Из экономичных конечно-разностных схем, получивших большое распространение, в дипломной работе рассмотрена схема метода дробных шагов Н.Н. Яненко. Данная схема при определенных условия может приводить к неустойчивости решения, от этого недостатка свободен следующий экономичный, абсолютно устойчивый метод переменных направлений с экстраполяцией В.Ф. Формалева. Среди неэкономичных, полностью неявных, а потому абсолютно устойчивых методов является метод матричной прогонки.

Для решения типовых примеров численными методами были написаны программы на языке программирования Turbo Pascal 6.0 и в математической системе MathCAD 7.0 Professional Edition (PRO).

Список используемой литературы

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.: БИНОМ. Лаборатория знаний, 2007. - 636 с.;

2. Березин И.С., Жидков Н.П. Методы вычислений. - М.: Наука, 1960, - 524 с.;

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, - М.: Высшая школа, 1997. – 486 с.;

4. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1966. – 400 с.;

5. Кабдыкайыр К. Курс высшей математики. – Алматы, Казахский университет, 2005. – 134 с.;

6. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах, - М.: Высшая школа, 2006. – 480 с.;

7. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Дифференциальные уравнения математической физики, Физматлит, Москва, 1962. – 710 с.;

8. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике. – М.: Высшая школа, 1994. – 416 с.;

9. Рихтмайер Р.Д. Разностные методы решения краевых задач, перевод с англ., - М.: Иностранная литература, 1960. – 262 с.;

10. Рябенький В.С. Введение в вычислительную математику. – М.: Наука, 1983.- 754 с.;

11. Самарский А.А. Теория разностных схем. - М.:Наука, 1983 – 726 с.;

12. Серавайкин С.Я., Секвенциальные модели математической физики, Алматы, 2004. – 192 с.;

13. Тихонов А.Н., Самарский А.А., Уравнения математической физики, Физматлит, Москва, 1966. – 735 с.;

14. Формалев В.И., Ревизников Д.Л. Численные методы, - М.: ФИЗМАТЛИТ, 2004. – 400 с.

Приложение

, где n=0, i=0..10

{Вычисления на нулевом слое}

{Вычисления на последующих слоях}

Размещено на Allbest.ru