
- •1. Дифференциальные уравнения в частных производных
- •1.1 Определение дифференциальных уравнений в частных производных параболического типа
- •1.2 Приведение уравнения второго порядка параболического типа к каноническому виду
- •1.3 Постановки задач для уравнений параболического типа
- •2. Численное решение дифференциальных уравнений
- •2.1 Основные определения и конечно-разностные схемы для дифференциальных уравнений параболического типа
- •2.1.1 Основные определения. Принцип построения разностных схем
- •2.1.2 Аппроксимация и сходимость разностных схем
- •2.1.3 Исследование устойчивости конечно-разностных схем
- •2.2 Конечно-разностный метод решения задач для уравнений параболического типа
- •2.2.1 Однородные и консервативные конечно-разностные схемы для задач теплопроводности с граничными условиями, содержащими производные
- •2.2.2 Неявно-явная конечно-разностная схема с весами. Схема Кранка-Николсона
- •2.2.3 Метод дробных шагов н.Н. Яненко
- •2.2.4 Метод переменных направлений с экстраполяцией в. Ф. Формалева
- •2.3 Численное решение определенных задач
2.1.2 Аппроксимация и сходимость разностных схем
Рассмотрим дифференциальную задачу в операторной форме (2.1) и операторную форму конечно-разностной схемы (2.3).
Введем норму сеточной функции с помощью выражения
 ,
,
 (2.9)
(2.9)
Определение
3. Конечно-разностная схема (2.3)
аппроксимирует дифференциальную задачу
на точном решении, если какая-либо норма
разности (не обязательно в виде (2.9))
 стремится к нули при
стремится к нули при :
:
 .
(2.10)
.
(2.10)
Определение
4. Конечно-разностная схема (2.3)
аппроксимирует дифференциальную задачу
на точном решении с порядком p по времени
и порядком q по пространственной
переменной, если какая-либо норма
разности
 удовлетворяет равенству
удовлетворяет равенству
 .
(2.11)
.
(2.11)
Таким образом, если конечно-разностная схема аппроксимирует дифференциальную задачу, то речь идет о близости дифференциального и конечно-разностного операторов в узлах сетки.
Из определения порядка аппроксимации ясно, что чем выше порядок аппроксимации, тем лучше конечно-разностная схема приближается к дифференциальной задаче. Это не означает, что решение по разностной схеме может быть так же близко к решению дифференциальной задачи, так как разностная схема может быть условно устойчивой или абсолютно неустойчивой вовсе.
Для
нахождения порядка аппроксимации
используется аппарат разложения в ряды
Тейлора точных (неизвестных, но
дифференцируемых) решений дифференциальной
задачи в узлах сетки (подчеркнем: значения
сеточной функции
 дискретны, следовательно, не дифференцируемы
и поэтому не разлагаются в ряды Тейлора).
дискретны, следовательно, не дифференцируемы
и поэтому не разлагаются в ряды Тейлора).
В
соответствии с определением порядка
аппроксимации проанализируем порядок
аппроксимации конечно-разностной схемы
(2.6), для чего эту схему запишем на точном
решении
 :
:
 (2.12)
(2.12)
Разложим
в ряды Тейлора по переменной х значения
 ,
, в окрестности узла
в окрестности узла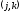 до
четвертой производной включительно, а
значение
до
четвертой производной включительно, а
значение – в Тейлора по переменной t в окрестности
узла
– в Тейлора по переменной t в окрестности
узла до второй производной включительно,
получим
до второй производной включительно,
получим
 (2.13)
(2.13)
 (2.14)
(2.14)
 (2.15)
(2.15)
Подставляя (2.13)-(2.15) в (2.12), находим
 .
.
Таким образом,
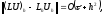
т. е. явная схема (2.6) для уравнения теплопроводности имеет первый порядок аппроксимации по времени и второй - по пространственной переменной. Аналогично, тот же порядок аппроксимации можно получить и для неявной схемы (2.8).
Определение
5. Решение
 ,
полученное с помощью конечно-разностной
схемы (2.3), сходится к точному решению
U, если какая-либо норма разности
,
полученное с помощью конечно-разностной
схемы (2.3), сходится к точному решению
U, если какая-либо норма разности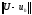 стремится к нулю при стремлении к нулю
сеточных характеристик
стремится к нулю при стремлении к нулю
сеточных характеристик :
:
 (2.16)
(2.16)
Определение
6. Конечно-разностная схема (2.3) имеет
p-й порядок сходимости (порядок точности)
по времени и q-й порядок сходимости по
пространственной переменной, если
какая-либо норма разности
 удовлетворяет равенству
удовлетворяет равенству
 .
.
Таким образом, порядок сходимости (порядок точности) характеризует близость конечно-разностного и точного (неизвестного) решения.
2.1.3 Исследование устойчивости конечно-разностных схем
Пусть
в конечно-разностной схеме (2.3) входные
данные
 получили возмущения и приняли значения
получили возмущения и приняли значения .
Тогда сеточная функция
.
Тогда сеточная функция также получит возмущение и примет
значение
также получит возмущение и примет
значение
Определение
7. Конечно-разностная схема (2.3) устойчива
по входным данным, если найдется такая
ограниченная константа
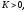 не зависящая от сеточных характеристик
не зависящая от сеточных характеристик и входные данные
и входные данные ,
что выполняется неравенство
,
что выполняется неравенство
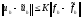 .
(2.17)
.
(2.17)
Таким
образом, понятие устойчивости
интерпритируется следующим образом:
конечно-разностная схема устойчива,
если для малых возмущений входных данных
(начально-краевых условий и правых
частей) конечно-разностная схема (2.3)
обеспечивает малые возмущения сеточной
функции
 ,
т.е. решение с помощью конечно-разностной
схемы находится под контролем входных
данных.
,
т.е. решение с помощью конечно-разностной
схемы находится под контролем входных
данных.
Если
во входных данных
 входят только начальные условия или
только краевые условия, или только
правые части, то говорят об устойчивости
соответственно по начальным условиям,
по краевым условиям или по правым частям.
входят только начальные условия или
только краевые условия, или только
правые части, то говорят об устойчивости
соответственно по начальным условиям,
по краевым условиям или по правым частям.
Определение
8. Конечно-разностная схема (2.3) называется
абсолютно устойчивой, если неравенство
(2.17) выполняется при любом соотношении
шагов
 и
и .
.
Определение
9. Конечно-разностная схема (2.3), неустойчивые
при любом соотношении шагов
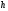 и
и называются абсолютно неустойчивыми.
называются абсолютно неустойчивыми.
Определение
10. Конечно-разностная схема (2.3) называется
условно устойчивой, если неравенство
(2.17) выполняется для сеточных характеристик
 и
и ,
на которые накладываются определенные
ограничения.
,
на которые накладываются определенные
ограничения.
Поскольку устойчивость является одной из основных характеристик конечно-разностных схем, то в данном параграфе рассматриваются различные методы исследования устойчивости конечно-разностных схем по начальным условиям. Наиболее распространенными методами исследования устойчивости являются следующие:
- метод гармонического анализа (Фурье);
- принцип максимума;
- спектральный метод;
- энергетический метод.
Каждый из этих методов имеет достоинства и недостатки.
Метод гармонического анализа. Из математической физики известно, что решение начально-краевых задач представляется в виде следующего ряда:
 ,
,
где
 - собственные значения, а
- собственные значения, а - собственные функции, получаемые из
решения соответствующей задачи
Штурма-Лиувиля, т. е. решение может быть
представлено в виде суперпозиции
отдельных гармоник
- собственные функции, получаемые из
решения соответствующей задачи
Штурма-Лиувиля, т. е. решение может быть
представлено в виде суперпозиции
отдельных гармоник ,
каждая из которых есть произведение
функции времени t и функции пространственной
переменной х, причем последняя по модулю
ограничена сверху единицей при любых
значениях переменной х.
,
каждая из которых есть произведение
функции времени t и функции пространственной
переменной х, причем последняя по модулю
ограничена сверху единицей при любых
значениях переменной х.
В
то же время функция времени
 ,
называемая амплитудной частью гармоники,
никак не ограничена, и, по всей вероятности,
именно амплитудная часть гармоник
является источником неконтролируемого
входными данными роста функции и,
следовательно, источником неустойчивости.
,
называемая амплитудной частью гармоники,
никак не ограничена, и, по всей вероятности,
именно амплитудная часть гармоник
является источником неконтролируемого
входными данными роста функции и,
следовательно, источником неустойчивости.
Таким образом, если конечно-разностная схема устойчива, то отношение амплитудной части гармоники на верхнем временном слое к амплитудной части на нижнем временном слое по модулю должно быть меньше единицы.
Если
разложить значение сеточной функции
 в
ряд Фурье по собственным функциям:
в
ряд Фурье по собственным функциям:
 (2.18)
(2.18)
где
амплитудная часть
 может быть представлена в виде произведения
может быть представлена в виде произведения
 ,
(2.19)
,
(2.19)
Un - размерный и постоянный сомножитель амплитудной части, а k - показатель степени (соответствующий номеру временного слоя) сомножителя, зависящего от времени, то, подставив (2.18) в конечно-разностную схему, можно по модулю оценить отношение амплитудных частей на соседних временных слоях.
Однако поскольку операция суммирования линейна и собственные функции ортогональны для различных индексов суммирования, то в конечно-разностную схему вместо сеточных значений достаточно подставить одну гармонику разложения (2.18) (при этом у амплитудной части убрать индекс n), т. е.
 ,
,
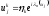 ,
,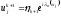 .
(2.20)
.
(2.20)
Таким образом, если конечно-разностная схема устойчива по начальным данным, то
 ,
(2.21)
,
(2.21)
т. е. условие (2.21) является необходимым условием устойчивости.
Исследование устойчивости методом гармонического анализа явной и неявной схем для уравнения теплопроводности. Подставим выражения (2.20) в явную конечно-разносную схему (2.6) для уравнения теплопроводности, получим
 ,
,
 (2.22)
(2.22)
Здесь использована формула, вытекающая из формулы Эйлера:
 ,
,
и
формула
 ,
причем
,
причем ,
поскольку
,
поскольку и
и .
.
В соответствии с (2.22) получаем выражение
 ,
,
 ,
,
или, с учетом (2.21), неравенство

Отсюда получаем следующие два неравенства:
 ,
,
из
которых правое выполнено всегда, а из
левого следует знаменитое условие
устойчивости Куранта: ,
или более жесткое для
,
или более жесткое для условие
условие
 (2.23)
(2.23)
Из
(2.23) следует, что явная схема для уравнения
теплопроводности условно устойчива с
условием (2.23), накладываемым на сеточные
характеристики
 и h.
и h.
Подставим теперь гармоники (2.20) в неявную конечно-разностную схему (2.8) для уравнения теплопроводности, получим
 ,
,

всегда, так как а и квадрат синуса больше нуля.
Следовательно,
неявная схема для уравнения теплопроводности
абсолютно устойчива, так как для
выполнения неравенства
 на
сеточные характеристики
на
сеточные характеристики и h не накладывалось никаких ограничений.
и h не накладывалось никаких ограничений.
Комплекс
 называют числом Куранта для уравнения
теплопроводности.
называют числом Куранта для уравнения
теплопроводности.
Принцип максимума. В математической физике известен принцип, в соответствии с которым решение начально-краевой задачи внутри расчетной области не может превышать значений искомой функции на пространственно-временной границе. Этот принцип положен в основу метода исследования устойчивости конечно-разностных схем, называемого принципом максимума.
Для его использования рассмотрим явную конечно-разностную схему (2.6) для уравнения теплопроводности в форме
 (2.24)
(2.24)
и
введем норму сеточной функции
 в виде
в виде .
.
Тогда из (2.24) получим
 (2.25)
(2.25)
 ,
(2.26)
,
(2.26)
то из (2.25) имеем неравенство
 ,
,
откуда, продолжая цепочку неравенств вплоть до начального условия, получим
 ,
(2.27)
,
(2.27)
где
 - начальное условие из (1.18).
- начальное условие из (1.18).
Неравенства (2.27) в вычислительной математике называют принципом максимума. Он является достаточным условием устойчивости явной схемы (2.24) для уравнения теплопроводности.
Таким образом, если выполнено условие Куранта (2.26), то из цепочки (2.27) видно, что значение сеточной функции на любом временном слое по норме не превысит начального условия, т. е. рассматриваемая схема устойчива по начальному условию, причем условие (2.26) является теперь не только необходимым в соответствии с методом гармонического анализа, но и достаточным.
Спектральный
метод исследования устойчивости.
Рассмотрим сеточные функции
 и
и ,
, ,
на двух временных слоях
,
на двух временных слоях и
и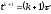 и представим конечно-разностную схему
в следующей операторной форме:
и представим конечно-разностную схему
в следующей операторной форме:
 ,
(2.28)
,
(2.28)
где S - оператор перехода от слоя tk к слою tk+1. Такой оператор можно построить не для всякой конечно-разностной схемы
(например, метод прогонки нельзя представить в форме (6.64)). Для явных конечно-разностных схем (2.6) оператор S представляется следующей матрицей перехода:
 .
.
Составим от левой и правой частей равенства (2.28) операцию нормы и используем свойство нормы: норма произведения операторов не превышает произведения норм, получим
 .
(2.29)
.
(2.29)
Если выполнено неравенство вида
 ,
(2.30)
,
(2.30)
то из условий (2.29) и (2.30) следует принцип максимума
 .
.
Таким образом, если схема устойчива, то норма оператора перехода S не превышает единицы и, следовательно, условие (2.30) является необходимым условием устойчивости конечно-разностных схем.
Энергетический метод исследования устойчивости конечно-разностных схем. Как видно из предыдущих разделов, метод гармонического анализа и спектральный метод являются необходимыми условиями устойчивости конечно-разностных схем, а принцип максимума - достаточным условием устойчивости. В данном пункте рассматривается один из самых мощных и распространенных методов - энергетический метод, развитый в работах А.А. Самарского и базирующийся на понятиях энергетического пространства с энергетической нормой, энергетического тождества (неравенства) и принципа максимума. Ниже будет показано, что условия, используемые в энергетическом методе, являются достаточными условиями устойчивости конечно-разностных схем.
Для понимания энергетического метода рассмотрим применение его с целью исследования устойчивости конечно-разностных схем при численном решении следующей первой начально-краевой задачи для уравнения теплопроводности с однородными краевыми условиями:
 ,
,
 ,
t > 0; (2.31)
,
t > 0; (2.31)
 ,
x = 0, t > 0; (2.32)
,
x = 0, t > 0; (2.32)
 ,
x = 1, t > 0; (2.33)
,
x = 1, t > 0; (2.33)
 ,
,
 ,
t = 0; (2.34)
,
t = 0; (2.34)
На сетке (2.2) будем аппроксимировать эту задачу с помощью явной (2.6) и неявной (2.8) конечно-разностных схем, записанных в векторно-операторной форме следующим образом:
 ,
(2.35)
,
(2.35)
 ,
(2.36)
,
(2.36)
где
конечно-разностный оператор
 аппроксимирует дифференциальный
оператор по пространственной переменной
x, т.е.
аппроксимирует дифференциальный
оператор по пространственной переменной
x, т.е.
 .
.
Энергетическое
пространство. Введем энергетическое
пространство HA сеточных функций
 ,
являющееся гильбертовым пространством,
в котором определено скалярное
произведение для двух элементов
,
являющееся гильбертовым пространством,
в котором определено скалярное
произведение для двух элементов и
и :
:
 ,
(2.37)
,
(2.37)
и, следовательно, с нормой
 .
(2.38)
.
(2.38)
Как
известно, гильбертово пространство -
это полное нормированное пространство,
в котором определено скалярное
произведение. Здесь полнота определяется
в том смысле, что если последовательность
сеточных функций
 сходится к своему пределу при
сходится к своему пределу при (в данном случае - к решению дифференциальной
задачи), то она является фундаментальной,
т.е. выполняется условие Коши
(в данном случае - к решению дифференциальной
задачи), то она является фундаментальной,
т.е. выполняется условие Коши
 .
(2.39)
.
(2.39)
Действительно, если конечно-разностная схема аппроксимирует дифференциальную задачу и устойчива, то по теореме эквивалентности решение с помощью конечно-разностной схемы сходится к решению дифференциальной задачи при измельчении сетки.
Для
двух сеточных функций
 и
и (двух элементов гильбертова пространства
HA) на различных сетках с шагами hn и hm
понятие полноты означает, что при
измельчении сетки, т. е. при
(двух элементов гильбертова пространства
HA) на различных сетках с шагами hn и hm
понятие полноты означает, что при
измельчении сетки, т. е. при (или
(или )
последовательности
)
последовательности и
и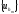 сходятся к одному и тому же пределу, т.
е. выполняется (2.39).
сходятся к одному и тому же пределу, т.
е. выполняется (2.39).
В дальнейшем потребуются следующие понятия, характеризующие конечно-разностные операторы: сопряженность, самосопряженность, положительная определенность.
Определение 11. Конечно-разностный оператор А* называется сопряженным оператору А, если выполняется равенство
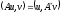 .
(2.40)
.
(2.40)
Например, если оператор А - симметрическая матрица с действительными элементами (А = АТ), то А - сопряженный оператор (это можно проверить непосредственно).
Определение. Конечно-разностный оператор А называется самосопряженным, если выполняется равенство
 .
(2.41)
.
(2.41)
Определение
12. Конечно-разностный оператор А
называется положительно определенным
![]() или положительно полуопределенным
или положительно полуопределенным
 на
гильбертовом пространстве сеточных
функций
на
гильбертовом пространстве сеточных
функций
 ,
если
,
если
 или
или
 .
(2.42)
.
(2.42)
Можно
показать, что разностный оператор
 является самосопряженным, т. е.
является самосопряженным, т. е.
 .
.
С
целью определения собственных функций
и собственных значений конечно-разностного
оператора А, рассмотрим вначале задачу
на собственные значения и собственные
функции оператора
 :
:
 (2.43)
(2.43)
Собственные
функции
 должны удовлетворять следующим условиям:
должны удовлетворять следующим условиям:
быть
ортогональными на отрезке
 при
при ,
т. е.
,
т. е.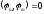 на
на при
при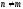 ;
;
удовлетворять однородным краевым уравнениям (2.32), (2.33);
их
число должно совпадать с числом
собственных значений
 .
.
Таким условиям удовлетворяют функции:
 ,
,
 ,
, ,
, ,
,
 ,
,
 ;
; .
(2.44)
.
(2.44)
Для
нахождения собственных значений
 подставим (2.44) в (2.43), получим
подставим (2.44) в (2.43), получим
 ,
,
 ,
,
 ,
,
 (2.45)
(2.45)
Из
(2.45) видно, что все собственные значения
оператора А отрицательны, а собственные
значения оператора
 положительны, т. е. оператор
положительны, т. е. оператор положительно
определен.
положительно
определен.
При исследовании устойчивости явной конечно-разностной схемы (2.35) энергетическим методом воспользуемся следующими тождествами:
 ;
;
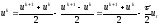 .
(2.46)
.
(2.46)
Умножим
скалярно явную схему (2.35) на вектор
 ,
получим
,
получим
 ,
,
или, после подстановки сюда тождеств (2.46),
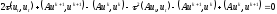 .
.
В силу самосопряженности оператора А и коммутативности скалярного произведения, последние два слагаемых сокращаются, после чего получим следующее энергетическое тождество:
 .
(2.47)
.
(2.47)
Если оператор
 ,
(2.48)
,
(2.48)
то из (2.47) получаем следующее энергетическое неравенство:
 ,
(2.49)
,
(2.49)
 ,
,
откуда сразу следует принцип максимума

являющийся достаточным условием устойчивости.
Если
теперь от неравенства (2.48) вычислить
любую норму
 ,
например норму, которая равна максимальному
по модулю собственному значению оператора
А, то с использованием выражения (2.45)
получим
,
например норму, которая равна максимальному
по модулю собственному значению оператора
А, то с использованием выражения (2.45)
получим

 ;
;
 ,
,
 .
(2.50)
.
(2.50)
Таким образом, условие устойчивости Куранта (2.33) явной конечно-разностной схемы для уравнения теплопроводности, выведенное с помощью метода гармонического анализа, является и достаточным условием.
Исследуем теперь устойчивость неявной конечно-разностной схемы (2.36) энергетическим методом, для чего к тождествам (2.46) добавим тождество
 (2.51)
(2.51)
Умножим
скалярно схему (2.36) на вектор
 ,
получим
,
получим
 ,
,
 ,
,
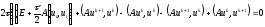 .
.
Таким образом, для неявной схемы энергетическое тождество имеет вид
 .
(2.52)
.
(2.52)
Здесь первое слагаемое всегда положительно определено, поэтому энергетическое неравенство имеет вид
 ,
,
 ,
(2.53)
,
(2.53)
откуда следует принцип максимума
 .
.
Таким
образом, неявная схема (2.36) безусловно
устойчива, так как оператор
 всегда положительно определен.
всегда положительно определен.
