- •9. Равномерное, равнопеременное и переменное движение по окружности. Аналогия между параметрами и уравнениями поступательного движения и движения по окружности.
- •2. Криволинейное движение
- •42. Политропический процесс. Уравнение политропы и его частные случаи.
- •Показатель политропы
- •Графики
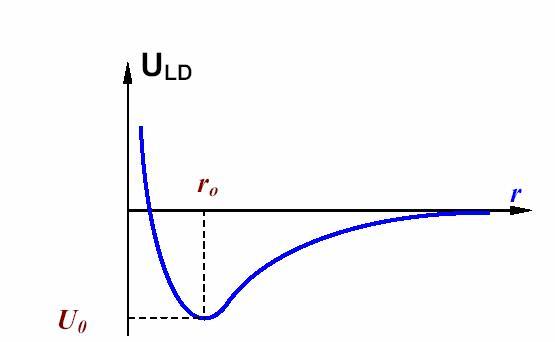
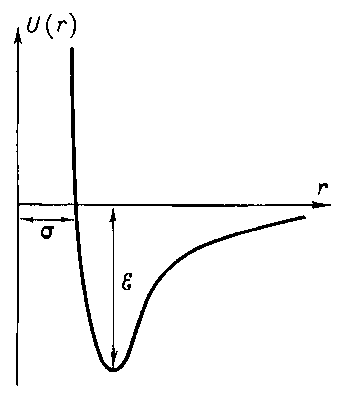
- •11. График потенциала Леннарда-Джонса.
- •31. Лемма о линейной независимости ортогональной системы. Процесс ортогонализации Грамма-Шмидта.
- •64. Вывод табличных производных. Производная постоянной.
- •Производная степенной функции.
- •Производная показательной функции.
- •Производная логарифмической функции.
- •Производные тригонометрических функций.
- •Производные гиперболических функций.
- •Производная обратной функции.
Показатель политропы
Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:
![]()
где р — давление, V — объем газа, n — «показатель политропы».
![]() .
Здесь
.
Здесь ![]() —
теплоёмкость газа в данном процессе,
—
теплоёмкость газа в данном процессе, ![]() и
и ![]() —
теплоемкости того же газа, соответственно,
при постоянном давлении и объеме.
—
теплоемкости того же газа, соответственно,
при постоянном давлении и объеме.
|
Различные
значения показателя политропы | ||
|
Значение показателя политропы |
Уравнение |
Описание процесса |
|
|
— |
Хотя этот случай не имеет практического значения для наиболее распространённых технических приложений, показатель политропы может принимать отрицательные значения в некоторых специальных случаях, рассматриваемых, например, в некоторых состояниях плазмы в астрофизике.[1] |
|
|
|
Это изобарный процесс (протекающий при постоянном давлении) |
|
|
|
Это изотермический процесс (протекающий при постоянной температуре) |
|
|
— |
Это квазиадиабатические процессы, протекающие, например, в двигателях внутреннего сгорания во время расширения газа |
|
|
— |
|
|
|
— |
Это изохорный процесс (протекающий при постоянном объёме) |
Графики
11. График потенциала Леннарда-Джонса.
Потенциал Леннард-Джонса (потенциал 6-12) — простая модель парного взаимодействия неполярных молекул, описывающая зависимость энергии взаимодействия двух частиц от расстояния между ними. Эта модель достаточно реалистично передаёт свойства реального взаимодействия сферических неполярных молекул и поэтому широко используется в расчётах и при компьютерном моделировании. Впервые этот вид потенциала был предложен Леннард-Джонсом в 1924 году.[1]
Потенциал Леннард-Джонса записывается в следующем виде:
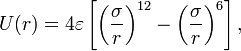
где ![]() —
расстояние между центрами частиц,
—
расстояние между центрами частиц, ![]() —
глубина потенциальной ямы,
—
глубина потенциальной ямы, ![]() —
расстояние, на котором энергия
взаимодействия становится равной нулю.
Параметры
—
расстояние, на котором энергия
взаимодействия становится равной нулю.
Параметры ![]() и
и ![]() являются
характеристиками атомов соответствующего
вещества. Характерный вид потенциала
показан на рисунке, его минимум лежит
в точке
являются
характеристиками атомов соответствующего
вещества. Характерный вид потенциала
показан на рисунке, его минимум лежит
в точке ![]() .
.
При
больших ![]() молекулы
притягиваются, что соответствует
члену
молекулы
притягиваются, что соответствует
члену ![]() в
формуле. Эту зависимость можно обосновать
теоретически, и обусловлена она силами
Ван-дер-Ваальса (диполь-дипольное
индуцированное взаимодействие).
в
формуле. Эту зависимость можно обосновать
теоретически, и обусловлена она силами
Ван-дер-Ваальса (диполь-дипольное
индуцированное взаимодействие).
На
малых же расстояниях молекулы отталкиваются
из-за обменного
взаимодействия(при
перекрытии электронных облаков молекулы
начинают сильно отталкиваться), чему
соответствует член ![]() .
Данный конкретный вид потенциала
отталкивания, в отличие от вида потенциала
притяжения, не имеет под собой
теоретического обоснования. Более
обоснованной является экспоненциальная
зависимость[источник не указан 980 дней].
Однако потенциал отталкивания
Леннард-Джонса более удобен в вычислениях,
так как
.
Данный конкретный вид потенциала
отталкивания, в отличие от вида потенциала
притяжения, не имеет под собой
теоретического обоснования. Более
обоснованной является экспоненциальная
зависимость[источник не указан 980 дней].
Однако потенциал отталкивания
Леннард-Джонса более удобен в вычислениях,
так как ![]() ,
что и оправдывает его применение.
,
что и оправдывает его применение.
|
|
|
Матан
31. Лемма о линейной независимости ортогональной системы. Процесс ортогонализации Грамма-Шмидта.

Ортогонализация Грама-Шмидта
Процесс Грама ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейнонезависимой системе ![]() строитсяортогональная система
строитсяортогональная система ![]() такая, что каждыйвектор bi линейно выражается через
такая, что каждыйвектор bi линейно выражается через ![]() , то есть матрица перехода от {ai} к {bi} ―верхнетреугольная матрица. При этом можно добиться того, чтобы система {bi} была ортонормированной ичтобы диагональные элементы матрицы перехода были положительны; этими условиями система {bi} иматрица перехода определяются однозначно.
, то есть матрица перехода от {ai} к {bi} ―верхнетреугольная матрица. При этом можно добиться того, чтобы система {bi} была ортонормированной ичтобы диагональные элементы матрицы перехода были положительны; этими условиями система {bi} иматрица перехода определяются однозначно.
Этот процесс применим также и к счётной системе векторов.
Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы впроизведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольнойматрицы с положительными диагональными элементами, что есть частный случай разложения Ивасавы.
Алгоритм
Полагают b1 = a1, и, если уже построены векторы ![]() , то
, то
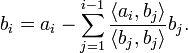
Геометрический смысл описанного процесса состоит в том, что на каждом шагу вектор bi являетсяперпендикуляром, восстановленным к линейной оболочке векторов ![]() до конца вектораai.
до конца вектораai.
Нормируя полученные векторы bi,
ci = bi / | bi |
получают искомую ортонормированную систему {ci}.