Выч. мат. Лекции. 6 семестр

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА.

ЛЕКЦИИ. ЧАСТЬ 2

Оглавление

7.3Апостериорная оценка погрешности квадратурных формул (правило Рунге) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

Глава 8. Методы решения задачи Коши для систем обыкновенных

8.2Многошаговые методы (методы Адамса) . . . . . . . . . . . . . . . . . 22

8.3Апостериорная оценка погрешности разностной схемы на шаге (правило Рунге) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

8.4Системы линейных дифференциальных уравнений первого порядка . 26

8.5Разностные схемы. Каноническая форма разностных схем . . . . . . . 28

8.6Порядок аппроксимации разностной схемы . . . . . . . . . . . . . . . . 28

1

Глава 7 Методы вычисления определенных интегралов

ВВЕДЕНИЕ.

Рассматриваются методы вычисления интегралов

b

Z

J(f) = p(x)f(x) dx:

a

Функция p(x) фиксирована, она называется весовой функцией и удовлетворяет

некоторым условиям. Исходя из определения интеграла можно предложить методы его приближенного вычисления. Нас будет интересовать точность вычисления интеграла

Пример. Интегрирование по частям интеграла

приводит к методу вычисления интеграла Jn:

Для больших значений n этот метод неприменим: обозначим через " = J0 ïî-

2

грешность вычисления значения J0, зависящую от точности задания числа e. Тогда

j Jnj = n!j"j;

èэта величина может быть больше значения jJnj при больших n.

Âоснове численных методов лежит теория интерполирования и аппроксимации функции f. Приближенное значение интеграла представимо в виде квадратурной

формулы:

m

X

J(f) Akf( k);

k=1

погрешность (методическая погрешность) квадратурной формулы, зависящая от выбора узлов, от способов вычисления коэффициентов Ak и от свойств функции f.

При построении квадратурной формулы отрезок [a; b] как правило разбивается на

X

p(x)f(x) dx = p(x)f(x) dx; x0 = a; xn = b:

Для каждого отрезка [xi 1; xi] строятся свои ¾малые¿ квадратурные формулы и в результате получают составные квадратурные формулы. Рассмотрим простейшие примеры квадратурных формул. Для простоты будем полагать p(x) 1;

1

xi = a + ih; i = 0; 1; : : : ; n; h = n(b a):

1.Квадратурная формула прямоугольников. На отрезке [xi 1; xi] выберем узел i.

Формула прямоугольников основана на замене функции f(x) кусочно-постоянной

3

функцией.

Оценка точности формулы прямоугольников. 1-а. Функция f 2 C1[a; b] è jf0(x)j M1.

xi

Z

Ri(f) = [f(x) f( i)] dx:

xi 1

Òàê êàê f(x) f( i) = f0( i)(x i), где значения i = i(x) находятся между значениями x и i, òî

выборе узлов i приходим к оценке

jRi(f)j M1h2:

1

При специальном выборе узлов i = xi 1 + 2h (квадратурная формула средних

1

прямоугольников) величина jRi(f)j 4M1h2:

Для составных квадратурных формул прямоугольников

jRi(f)j M1(b a)h;

а для формулы средних прямоугольников

1

jRi(f)j 4M1(b a)h:

Èòàê ïðè f 2 C1[a; b] квадратурные формулы прямоугольников имеют первый порядок малости относительно величины шага h.

1-б. Функция f 2 C2[a; b] è jf00(x)j M2.

В этом случае f(x) f( i) = f0( i)(x i) + 12f00( )(x i)2, где значения = (x)

4

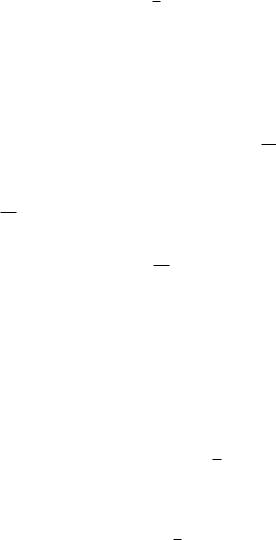
находятся между значениями x и i. Òàê êàê (x i)2 0, то для оценки интеграла

xi

Z

f00( (x))(x i)2 dx

xi 1

следует применить теорему о среднем (смотри, например, С. М. Никольский, ¾Курс математического анализа¿, т. I, глава 9: Определенный интеграл Римана):

1

При специальном выборе i = xi 1 + 2h (формула средних прямоугольников)

xi

Z

f0( i)(x i) dx = 0;

xi 1

xi

Z

jf00( (x))(x i)2 dxj M2 121 h3:

xi 1

1

Тогда jRi(f)j 24M2h3, и для составной формулы средних прямоугольников

jRi(f)j 241 M2(b a)h2:

Для функция f 2 C2[a; b] квадратурная формула средних прямоугольников имеет второй порядок точности.

2. Квадратурная формула трапеций.

Для функции f, заданной на отрезке [a; b] строится сплайн класса S1;0 (т.е. непре- рывная кусочно-линейная функция) по системе узлов xi = a + ih.

На каждом частичном отрезке f~(x) = fi 1 + h1 (fi fi 1)(x xi 1) = L1(f; x); ãäå L1(f; x) интерполяционный полином Лагранжа. Ясно, что

xi

Z

f~(x) dx = 12(fi 1 + fi)h:

xi 1

5

xi 1

Полагая, что значения L2;i и f близки, получаем малую квадратурную формулу Симпсона: xi

Z

1

f(x) dx 6[fi 1 + 4fi 12 + fi]:

xi 1

6

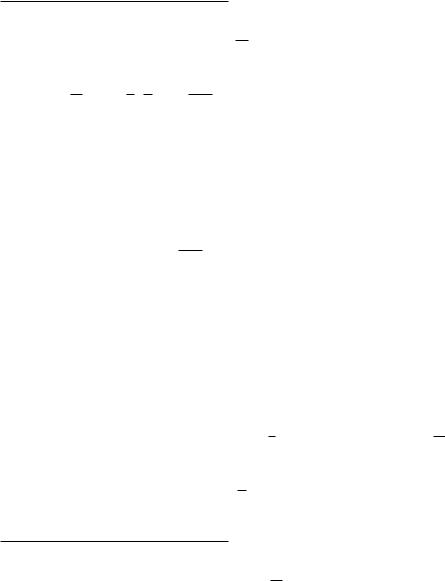
Åñëè f 2 C3[a; b] è jf000(x)j M3, òî

1

jf(x) L2(f; x)j 3!M3j(x xi 1)(x xi 12 )(x xi)j

11 h 1

èjRi(f)j 3!M32 4( 2 )4 = 192M3h4:

Для составной формулы Симпсона

ai=1

1

получаем оценку jR(f)j 192M3(b a)h3:

Легко заметить, что для полиномов третьей степени малая формула Симпсона

i 1

для этого достаточно представить полином P3(x) â âèäå

P3(x) = P3(xi 12 ) + P30(xi 12 )(x xi 12 ) + 12P300(xi 12 )(x xi 12 )2 + 3!1 P3000(xi 12 )(x xi 12 )3

Åñëè f 2 C4[a; b] è jf(4)(x) Mj, òî

f(x) = P3(x) + 4!1 f(4)( i)(x xi 12 )4;

и легко получить оценку точности формулы Симпсона. Мы получим более точную оценку. Для функции f 2 C4[a; b] построим полином третьей степени, совпадающий

со значениями функции f(x) в узлах xi 1; xi 12 ; xi. В частности таким полиномом является полином Эрмита H3(x):

H3(xi 1) = fi 1; H3(xi 12 ) = fi 12 ; H30 (xi 12 ) = f0(xi 12 ); H3(xi) = fi:

7

è òàê êàê (x xi 1)(x xi 12 )2(x xi) 0 (не меняет знак на [xi 1; xi], òî

xi

Z

Ri(f) = 4!1 f(4)( i) (x xi 1)(x xi 12 )2(x xi) dx = 4!1 f(4)( i)1201 h5; i 2 [xi 1; xi]

xi 1

1

è jRi(f)j 2880M4(b a)h4.

Для составной квадратурной формулы Симпсона при условии f 2 C4[a; b] верна

оценка

jR(f)j 28801 M4(b a)h4:

7.1Интерполяционные квадратурные формулы

В этом параграфе рассматривается случай, когда функция jf(x)j заменяется алгебраическим интерполяционным полиномом степени (n 1), а узлы x1; x2; : : : ; xn заданы. Ясно, что получаемая квадратурная формула точна для полиномов степени (n 1) или как говорят, имеет алгебраическую степень точности (n 1).

Для вычисления коэффициентов Ak можно применить метод неопределенных коэффициентов: достаточно потребовать, чтобы для j = 0; 1; : : : ; (n 1) выполнялись

равенства

ak=1

f 2 Cn[a; b] с оценкой jf(n)(x)j Mn оценивается величиной jJ(f) Pnk=1 Akf(xk)j

8

1Rb

n!Mn a p(x)j!n(x)j dx:

Для составных квадратурных формул степень интерполяционных полиномов, как правило, не велика.

Интерполяционные квадратурные формулы с равноотстоящими узлами называют формулами типа Ньютона-Котеса.

Метод неопределенных коэффициентов применяется и в случае, когда функция f(x) хорошо приближается линейными комбинациями линейно-независимых на [a; b]

функциями 'k(x).

7.2Квадратурные формулы типа Гаусса

В этом параграфе мы рассмотрим квадратурные формулы

для непрерывных на [a; b] функций f(x). Требуется найти узлы xk и коэффициенты Ak из условия, чтобы получаемые квадратурные формулы имели бы наивысший возможный алгебраический порядок точности.

Так как число неизвестных xk è Ak равно 2n, то можно рассчитывать на определение 2n коэффициентов полиномов, т.е. на то, что порядок точности равен 2n 1. Построение таких квадратурных формул опирается на свойства полиномов ортогональных на [a; b] со знакопостоянной весовой функцией p(x) 0, т.е. полиномов

n(x) таких что

Доказательство. Обозначим x1; x2; : : : ; xm все нули полинома n(x), расположен-

ные на [a; b] и имеющие нечетные кратности 1; 2; m.

Предположим, что m < n. Обозначим Qm(x) = (x x1)(x x2) : : : (x xm). Тогда

9