- •Министерство образования Российской Федерации
- •I. Численное интегрирование
- •1.1. Постановка задачи
- •1.2. Квадратурная формула. Квадратурный процесс
- •Из последнего равенства следует, что последовательность функционалов погрешности не может равномерно сходиться к нулю при.
- •1.3. Интерполяционная квадратурная формула
- •Для любой таблицы узлов :, используя формулу (8), получаем
- •1.4. Квадратурные формулы Ньютона-Котеса
- •Формула трапеций
- •Формула Симпсона (парабол)
- •Формула трех восьмых
- •1.5. Квадратурные формулы Гаусса
- •1.6. Квадратурные формулы с весом
- •Многочлен Якоби определяется формулой
- •1.7. Локально-интерполяционные (составные) квадратурные формулы
- •Правило трапеций
- •Правило Симпсона (парабол)
- •Варианты заданий
- •II. Численное дифференцирование
- •2.1. Постановка задачи. Применение интерполяционного многочлена Лагранжа
- •2.2. Сходящиеся формулы численного дифференцирования
- •Формула численного дифференцирования (36) называется сходящейся, еслипри для любой функции(в любой точке гладкости функции).
Варианты заданий
|
№ варианта |
|
|
|
№ варианта |
|
|
|
|
1 |
|
0 |
1 |
21 |
|
|
0,1 |
|
2 |
|
0 |
1 |
22 |
|
0,2 | |
|
3 |
|
0 |
1 |
23 |
0,3 | ||
|
4 |
|
1 |
2 |
24 |
0,4 | ||
|
5 |
|
0 |
|
25 |
0,5 | ||
|
6 |
|
1 |
2 |
26 |
0,6 | ||
|
7 |
|
0 |
1 |
27 |
0,7 | ||
|
8 |
|
0 |
|
28 |
0,8 | ||
|
9 |
|
0 |
|
29 |
0,9 | ||
|
10 |
|
0 |
|
30 |
1,0 |
|
№ варианта |
|
|
|
№ варианта |
|
|
|
|
11 |
|
0 |
|
31 |
|
|
0,1 |
|
12 |
|
0 |
|
32 |
0,2 | ||
|
13 |
|
0 |
1 |
33 |
0,3 | ||
|
14 |
|
0 |
1 |
34 |
0,4 | ||
|
15 |
|
0 |
1 |
35 |
0,5 | ||
|
16 |
|
0 |
1 |
36 |
0,6 | ||
|
17 |
|
2 |
3 |
37 |
0,7 | ||
|
18 |
|
2 |
3 |
38 |
0,8 | ||
|
19 |
|
2 |
3 |
39 |
0,9 | ||
|
20 |
|
1 |
2 |
40 |
1,0 |
Приложение. Для выполнения задания можно использовать следующие процедуры (на языке Паскаль):
1. Процедура simps, реализующая алгоритм правила Симпсона (парабол):
Procedure simps(a,b:real; var n:longint; var y:real);
{Входные параметры:
a – левый конец отрезка интегрирования;
b – правый конец отрезка интегрирования;
n - число частичных отрезков разбиения.
Выходные параметры:
y – значение интеграла.
Здесь f имя функции, вычисляющей значения подинтегральной функции.}
var
i :longint;
h,x :real;
begin
h:=(b-a)/n; y:=0; x:=a;
for i:=1 to n do
begin y:=y+f(x)+4*f(x+0.5*h)+f(x+h); x:=x+h end;
y:=y*h/6
end;
2. Процедура gauss, реализующая алгоритм составной формулы Гаусса с пятью узлами:
Procedure gauss(a,b:real; var n:word; var y:real);
{Входные параметры:
a – левый конец отрезка интегрирования;
b – правый конец отрезка интегрирования;
n - число частичных отрезков разбиения.
Выходные параметры:
y – значение интеграла.
Здесь f – имя функции, вычисляющей значения подинтегральной функции;
vec – одномерный массив (type vec=array[1..5]of real).}
var
i,j :word;
h,x,x1 :real;
ag,xg :vec;
z :real;
begin
ag[1]:=0.2369268850; xg[1]:=-0.9061798459;
ag[2]:=0.4786286705; xg[2]:=-0.5384693101;
ag[3]:=0.5688888889; xg[3]:=0.0;
ag[4]:=ag[2]; xg[4]:=-xg[2];
ag[5]:=ag[1]; xg[5]:=-xg[1];
h:=(b-a)/n; z:=0; x1:=a+0.5*h;
for j:=1 to n do
begin
for i:=1 to 5 do
begin x:=x1+0.5*h*xg[I]; z:=z+ag[i]*f(x); end;
x1:=x1+h
end;
y:=z*0.5*h
end;
II. Численное дифференцирование
2.1. Постановка задачи. Применение интерполяционного многочлена Лагранжа
Пусть
на отрезке
![]()
![]() R
определена достаточно гладкая функция
R
определена достаточно гладкая функция
![]()
![]() и требуется вычислить в точке
и требуется вычислить в точке![]() ее производную
ее производную![]()
![]() .
Если функция
.
Если функция![]() задана таблично или имеет сложное
аналитическое выражение, то непосредственное
дифференцирование невозможно. Поэтому
строят приближенные формулы численного
дифференцирования.
задана таблично или имеет сложное
аналитическое выражение, то непосредственное
дифференцирование невозможно. Поэтому
строят приближенные формулы численного
дифференцирования.
Один
из универсальных способов конструирования
формул численного дифференцирования
состоит в том, что по функции
![]() и узлам
и узлам![]() строят интерполяционный многочлен
Лагранжа (6)
строят интерполяционный многочлен
Лагранжа (6)![]() и полагают
и полагают
![]()
Разность
![]()
называется погрешностью формулы численного дифференцирования (33).
Для
получения оценок погрешности формулы
(33) для заданного
![]() существования
производной
существования
производной
![]() недостаточно. Обычно требуется выполнение
условия
недостаточно. Обычно требуется выполнение
условия![]() ,
,![]() .
.
Замечание 9.
Для конструирования формул численного
дифференцирования можно также использовать
интерполяционные сплайны. В вычислительной
практике для вычисления![]() и
и![]() обычно используют интерполяционный
естественный кубический сплайн
обычно используют интерполяционный
естественный кубический сплайн![]() :
:![]()
Приведем простейшие формулы численного дифференцирования.
1)
![]()
![]()
Если
![]() ,
то
,
то![]()
2)
![]()
![]()
Если
![]() ,
то
,
то![]()
3)
![]()
![]()
Если
![]() ,
то
,
то![]()
Представления
погрешности (34) формулы численного
дифференцирования (33), выражаемые через
производные функции
![]() ,
удается найти только в частных случаях.
Общая оценка погрешности формулы (33)
определяется следующей теоремой.
,
удается найти только в частных случаях.
Общая оценка погрешности формулы (33)
определяется следующей теоремой.
Теорема 4.
Пусть ![]() ,
,![]()
![]() .Тогда существуют такие константы
.Тогда существуют такие константы
![]() ,
зависящие только от
,
зависящие только от![]() и независящие от шага
и независящие от шага![]() и функции
и функции![]() ,
что
,
что
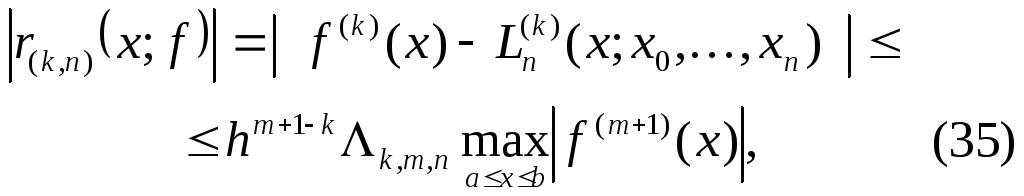
где
![]() - интерполяционный многочлен Лагранжа(6) и
- интерполяционный многочлен Лагранжа(6) и
![]() .
.
Замечание 10.Оценка (35) с постоянными![]() сильно завышена и редко используется
на практике. Однако оценка (35) полезна
тем, что она устанавливает скорость
убывания погрешности относительно шага
сильно завышена и редко используется
на практике. Однако оценка (35) полезна
тем, что она устанавливает скорость
убывания погрешности относительно шага![]() на всем отрезке
на всем отрезке![]() при фиксированных значениях параметров
при фиксированных значениях параметров![]() (
(![]() ).
Шаг
).
Шаг![]() является основным параметром, которым
распоряжается вычислитель.
является основным параметром, которым
распоряжается вычислитель.