
- •Министерство образования Российской Федерации
- •I. Численное интегрирование
- •1.1. Постановка задачи
- •1.2. Квадратурная формула. Квадратурный процесс
- •Из последнего равенства следует, что последовательность функционалов погрешности не может равномерно сходиться к нулю при.
- •1.3. Интерполяционная квадратурная формула
- •Для любой таблицы узлов :, используя формулу (8), получаем
- •1.4. Квадратурные формулы Ньютона-Котеса
- •Формула трапеций
- •Формула Симпсона (парабол)
- •Формула трех восьмых
- •1.5. Квадратурные формулы Гаусса
- •1.6. Квадратурные формулы с весом
- •Многочлен Якоби определяется формулой
- •1.7. Локально-интерполяционные (составные) квадратурные формулы
- •Правило трапеций
- •Правило Симпсона (парабол)
- •Варианты заданий
- •II. Численное дифференцирование
- •2.1. Постановка задачи. Применение интерполяционного многочлена Лагранжа
- •2.2. Сходящиеся формулы численного дифференцирования
- •Формула численного дифференцирования (36) называется сходящейся, еслипри для любой функции(в любой точке гладкости функции).
1.6. Квадратурные формулы с весом
Часто удобно исходный интеграл (1) записывать в виде
![]()
где
![]() -
некоторая заданная функция, называемаявесом. Обычно требуют, чтобы
интеграл
-
некоторая заданная функция, называемаявесом. Обычно требуют, чтобы
интеграл![]() абсолютно сходился и
абсолютно сходился и![]() В разложении на множители функции
В разложении на множители функции![]() функцию
функцию![]() выбирают
так, чтобы она обладала достаточно
высоким порядком гладкости на
выбирают
так, чтобы она обладала достаточно
высоким порядком гладкости на![]() ,
при этом весовая функция
,
при этом весовая функция![]() должна содержать все «особенности»
подинтегральной функции
должна содержать все «особенности»
подинтегральной функции![]() и быть по возможности наиболее простой.
и быть по возможности наиболее простой.
В этом случае интерполяционная квадратурная формула (7)-(8) принимает вид
![]()
где
![]()
Приведем
пример квадратурной формулы Гаусса с
весовой функцией Якоби ![]() ,позволяющей
учитывать степенные особенности
интегрируемой функции на концах отрезка.
Отрезок
,позволяющей
учитывать степенные особенности
интегрируемой функции на концах отрезка.
Отрезок ![]() приведем к отрезку
приведем к отрезку ![]() и построим
интерполяционную квадратурную формулу
и построим
интерполяционную квадратурную формулу
![]()
где
![]() -корни многочлена
Якоби
-корни многочлена
Якоби ![]() .
.
Многочлен Якоби определяется формулой
![]()
Многочлены
Якоби (23) ортогональны на отрезке
![]() с весом
с весом![]() и для любого многочлена
и для любого многочлена![]() степени
меньшей
степени
меньшей![]()
![]()
![]()
С помощью теоремы
3 получаем, что алгебраический порядок
точности квадратурной формулы (22) равен
![]() .
.
Квадратурная формула
(22) содержит два параметра
![]() и
и![]() ,
из нее могут быть получены специализированные
квадратурные формулы, соответствующие
распространенным видам степенных
особенностей (см.[3]). В справочниках
приведены квадратурные формулы Гаусса
с другими весами.
,
из нее могут быть получены специализированные
квадратурные формулы, соответствующие
распространенным видам степенных
особенностей (см.[3]). В справочниках
приведены квадратурные формулы Гаусса
с другими весами.
1.7. Локально-интерполяционные (составные) квадратурные формулы
Для повышения
точности квадратурных формул используют
прием, идея которого восходит к римановым
интегральным суммам. Отрезок интегрирования
![]() разбивают на некоторое число частичных
отрезков, на каждом из которых применяют
квадратурную формулу с небольшим числом
узлов. В качестве параметра квадратурного
процесса теперь используют число
частичных отрезков.
разбивают на некоторое число частичных
отрезков, на каждом из которых применяют
квадратурную формулу с небольшим числом
узлов. В качестве параметра квадратурного
процесса теперь используют число
частичных отрезков.
Разобьем отрезок
![]() на
на![]() частичных отрезков точками
частичных отрезков точками![]() .
Для вычисления интеграла на каждом
частичном отрезке
.
Для вычисления интеграла на каждом
частичном отрезке![]()
![]() применим интерполяционную квадратурную
формулу с
применим интерполяционную квадратурную
формулу с![]() узлами
узлами![]() и
и
коэффициентами
![]()
![]() .
Получим квадратурную формулу
.
Получим квадратурную формулу
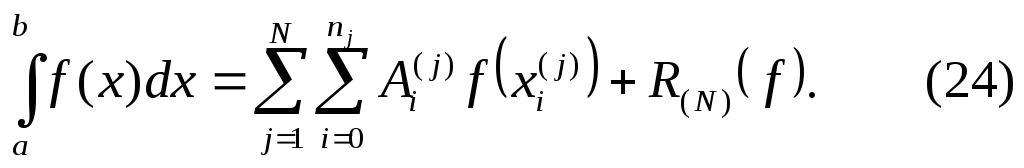
Пусть
![]() и
и![]() ,
тогда для погрешности квадратурной
формулы (24) имеет место оценка
,
тогда для погрешности квадратурной
формулы (24) имеет место оценка
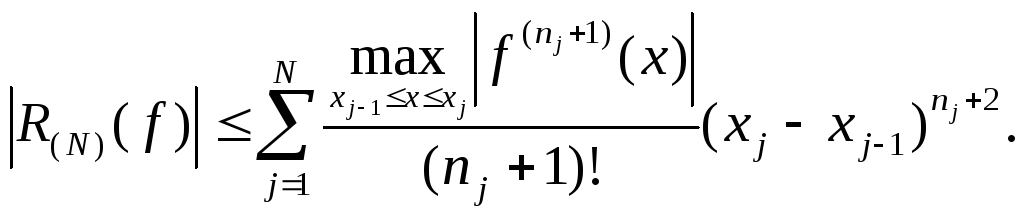
Квадратурная формула (24) называется локально-интерполяционнойилисоставной.
Наиболее часто
формула (24) используется в случае, когда
отрезок
![]() разбит на частичные отрезки равной
длины
разбит на частичные отрезки равной
длины![]() и на каждом частичном отрезке используется
квадратурная формула Ньютона-Котеса с
и на каждом частичном отрезке используется
квадратурная формула Ньютона-Котеса с![]() узлами. Из (24) получаем при
узлами. Из (24) получаем при![]() ,
,![]() и
и![]()
![]() локально-интерполяционную квадратурную
формулу
локально-интерполяционную квадратурную
формулу
![]()
где
![]()
Сумма абсолютных величин коэффициентов формулы (26)
![]()
не зависит от
числа частичных отрезков
![]() .
.
Оценка погрешности квадратурной формулы (25) имеет вид
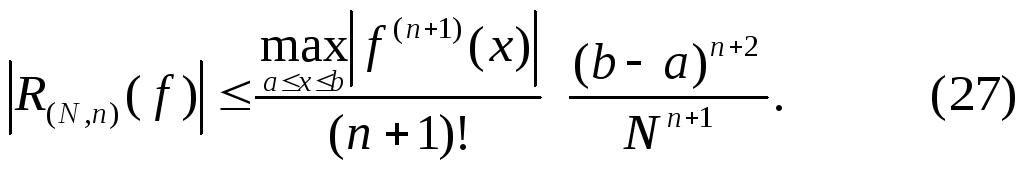
Из теоремы 2 и
(27) следует, что квадратурный процесс,
порожденный локально-интерполяционной
квадратурной формулой (25), является
сходящимся при
![]() (со скоростью
(со скоростью![]() на функциях из класса
на функциях из класса![]() ).
).
Приведем простейшие составные квадратурные формулы, часто применяемые в практике.
