
Ankilov
.pdfВидим, что система имеет множество решений
G A, B,C : A 3 , B 3 ,C , R .
Выбираем одно решение из G при 13 , тогда
u (x) 1 x 1 x2. |
|
|
|
|
||||||
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk 1, находим |
|
Аналогично, используя формулу u |
k |
A |
A x ... A |
|
||||||
|
|
|
0 |
1 |
|
k 1 |
|
|||
u2 (x) 1 x 1 x3 , u3 (x) 1 x 1 x4 , u4 (x) 1 x 1 x5 |
, u5 (x) 1 x 1 x6 . |
|||||||||
4 |
5 |
|
|
|
|
|
|
6 |
|
7 |
Пример 2. Построить u0 (x) и систему из трех пробных функций для |
||||||||||
задачи с краевыми условиями |
|
|
|
|
|
|
|
|
|
|
y(0) |
|
|
|
1, |
|
|
|
|
||
y (0) |
|
|
|
(2.28) |
||||||
|
|
|
|
|
2. |
|
|
|||
y(2) |
y (2) |
|
|
|
||||||
Решение. Если u0 (x) , то условия (2.28) приводят к несовместной системе |
||||||||||
|
A 1, |
|
|
|
|
|
|
|||
|
A 2. |
|
|
|
|
|
|
|||
Предположим, что u0 A Bx , тогда u0 B и условия (2.28) дают |
||||||||||
A B 1, |
A B |
1, |
|
A B |
1, |
|||||
|
|
|
|
|
2, |
|
0 |
1, |
||
A 2B B 2, |
A B |
|
|
|||||||
тоже несовместную систему. |
|
|
|
|
|
|
|
|
|
|
Полагаем u0 A Bx Cx2 , тогда u0 |
B 2Cx и условия (2.28) дают |
|||||||||
A B 1, |
A B |
1, |
|
A B |
1, |
|||||
|
|
|
|
|
2, |
|
0 |
1, |
||
A 2B B 2, |
A B |
|
|
|||||||
которая несовместна. |
|
|
|
|
|
|
|
|
|
|
Ищем u0 (x) в виде u0 A Bx Cx2 |
Dx3 , тогда u0 B 2Cx 3Dx2 , и из |
|||||||||
(2.28) имеем |
|
|
|
|
|
|
|
|
|
|
A B 1, |
|
|
|
|
|
|
|
A B 1, |
||
|
4C 12D 2, |
|
|
|
||||||
A 2B 4C 8D B |
|
A B 4D 2. |
||||||||
Решаем полученную систему методом Гаусса в матричной форме, чтобы найти все решения системы.
Прямой ход метода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A B C D |
|
|
|
A B C D |
A D C B |
|
|
||||||||||
1 |
1 |
0 |
0 |
|
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
0 0 |
1 |
|
1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
~ |
|
|
|
|
|
|
~ |
|
|
|
. |
|
1 |
0 |
4 |
|
|
|
0 |
0 |
0 |
4 |
|
|
|
4 0 |
0 |
|
|
1 |
|
2 |
|
|
1 |
0 |
|
1 |
|||||||||
Видим, что система |
|
совместна, ибо ранг |
|
матрицы системы rg равен рангу |
|||||||||||||
расширенной матрицы и равен 2. Так как число неизвестных системы, равное
31
четырем, больше rg 2, то система неопределена, и все множество решений |
|||||||||||
G0 системы получаем обратным ходом |
|
метода |
|
Гаусса, |
придавая двум |
||||||
неизвестным C и B произвольные значения. Получаем |
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
; |
1 |
|
G0 (A, B,C, D) : A 1 1, B 1,C 2 , D |
4 |
, 2 R . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Выбираем решение из G0 при 1 |
2 |
0 . Тогда |
|
|
|
|
|
||||
u0 (x) 1 |
1 |
x |
3 |
. |
|
|
|
|
|
||
4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Определяем теперь u1 (x) . |
Если |
u1 (x) A 0 , |
то |
однородные условия, |
|||||||
соответствующие условиям (2.28), выполняются при |
|
A 0 , что недопустимо. |
|||||||||
Пусть u1 (x) A Bx , u1 (x) B , |
и из однородных условий, соответствующих |
||||||||||
условиям (2.28), имеем |
|
|
|
|
|
|
|
|
|
|
|
A B |
0, |
|
A |
B 0 . |
|
|
|
|
|
||
|
0, |
|
|
|
|
|
|||||
A B |
|
|
|
|
|
|
|
|
|
|
|
Эта система неопределена, ее множество решений |
|
|
||||||
|
G1 (A, B) : A , B ; |
R . |
|
|
||||
Выбираем одно ненулевое решение при 1, |
тогда u1 (x) 1 x . |
|
||||||
Ищем u2 (x). Пусть u2 (x) A Bx Cx 2 |
|
(C 0 ), тогда |
u2 D 2Cx |
и |
||||
однородные условия дают систему |
|
|
|
|
|
|
||
|
|
A |
B 0, |
|
|
|
|
|
|
|
|
B 0C 0. |
|
|
|
||
|
|
A |
|
|
|
|||
Решая ее методом Гаусса, находим множество решений |
|
|
||||||
G2 (A, B,C) : A 1, B 1,C 2 ; 1, 2 R . |
|
|||||||
Выбирая одно |
ненулевое решение (C 0 ), |
при 1 2 |
1, получаем |
|||||
u2 (x) 1 x x2 . |
|
u3 (x) A Bx Cx 2 Dx3 |
|
|
||||
Находим |
u3 (x) . |
Если |
( D 0 ), |
то |
||||
u3 (x) B 2Cx 3Dx2 , и из однородных условий имеем систему |
|
|||||||
|
|
A B 0, |
|
|
A B 0, |
|
|
|
|
|
|
|
|
D 0, |
|
|
|
|
A B 0C 4D 0, |
|
|
|
|
|||
которая противоречит условию D 0 . |
|
|
|
|
|
|||
Пусть |
теперь |
u3 (x) A Bx Cx2 |
Dx3 Ex4 |
( E 0 ), тогда |
||||
u3 (x) B 2Cx 3Dx2 |
4Ex3 , и из однородных условий получаем систему |
|
||||||
|
A B |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
12D 32E 0, |
|
|
A 2B 4C 8D 16E B 4C |
|
|
||||||
A B 0,
A B 0C 4D 16E 0.
32
Решая ее методом Гаусса, получаем множество решений |
|
|
G3 (A, B,C, D, E) : A 1, B 1,C 2 , D 4 3 , E 3 ; |
1, 2 , 3 R . |
|
Выбирая одно ненулевое решение ( E 0 ) при 1 1, |
2 |
1, 3 1, имеем |
u3 (x) 1 x x2 4x3 x4 .
II. Подчеркнем, что если пробные функции выбираются на множестве многочленов, то их всегда можно найти методом неопределенных коэффициентов, причем неоднозначно. Например, в возможные системы пробных функций ui (x) можно включить многочлены
или |
|
|
um i (x) (x a)n1 i (b x)n2 |
, i 0,1,2, |
|
(2.29) |
||||||
|
|
u m i (x) (x a)n1 (b x)n2 i , i 0,1,2, , |
|
|
||||||||
|
|
|
|
(2.30) |
||||||||
где |
|
1, |
если a1 0; |
|
1, |
если |
b1 0; |
|
|
|
||
n1 |
|
n2 |
m n1 |
n2 |
l, |
|||||||
|
если |
a1 0; |
|
если |
b1 0; |
|||||||
|
|
2, |
|
2, |
|
|
|
|||||
а остальные функции |
u1 (x),...,um (x) |
следует определить среди многочленов |
||||||||||
P0 (x), , Pl 1 (x) методом неопределенных коэффициентов.
Пример 3. Построить систему пробных функций для задачи (2.2) с однородными краевыми условиями
y(0) y (0) 0,y(1) y (1) 0.
Решение. Так как n1 n2 4 , то из примера 1 выписываем первые две
пробные функции |
u (x) 1 x 1 x2 , |
u |
2 |
(x) 1 x 1 x3 |
(все |
|
многочлены |
||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
порядка меньше 4, удовлетворяющие краевым условиям). |
|
|
|
|
|
|
|
||||||||||||||||||||
Таким образом, учитывая, |
что |
n1 2, n2 |
2 , пробное |
решение можно |
|||||||||||||||||||||||
искать в виде |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
(x) C |
|
x |
x |
2 |
|
C |
|
|
x |
x |
3 |
|
n |
|
(1 x) |
2 |
x |
k 1 |
, |
||||||
n |
1 |
3 |
|
|
|
1 |
4 |
|
|
C |
k |
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
k 3 |
|
|
|
|
|
|
|
||||
если функции uk (x) |
(k 3) взять в виде (2.29). Если же в виде (2.30), то |
||||||||||||||||||||||||||
y |
|
(x) C |
|
x |
1 |
x |
2 |
|
C |
|
|
x |
1 |
x |
3 |
|
n |
|
(1 x) |
k 1 |
x |
2 |
. |
||||
n |
1 |
3 |
|
|
|
1 |
4 |
|
|
C |
k |
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
k 3 |
|
|
|
|
|
|
|
||||
III. При выборе систем поверочных функций полезно вспомнить о системах функций, ортогональных на некотором отрезке. Например, известно [3], что многочлены Лежандра, определяемые формулой
P (t) |
1 d n |
(t 2 1)n , |
n 0,1, 2,... |
(2.31) |
||
|
|
|
||||
n |
2n n! dt n |
|
|
|
||
|
|
|
|
|||
33

ортогональны на [–1,1]. Так что, если в качестве поверочных функций Wk (x)
решено взять, например, первые пять многочленов Лежандра, ортогональных на a, b , то в первые пять выражений из (2.31):
W P (t) 1, |
W |
P (t) t, |
W |
P (t) 1 |
(3t 2 |
1), |
|||||||||
|
1 |
0 |
|
|
2 |
|
1 |
|
|
3 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
P (t) 1 |
(5t3 3t), |
W P (t) 1 (35t 4 30t 2 |
3) |
|||||||||||
4 |
|
3 |
2 |
|
|
|
|
5 |
4 |
8 |
|
|
|
|
|
следует подставить |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
a b |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
t |
|
|
x |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
b a |
|
|
|
|
|
|||
IV. Важным источником для построения ортогональных на [a, b] пробных
функций является множество решений задачи, называемой задачей на собственные значения для дифференциального оператора L[ y] y [3].
Рассмотрим конкретный пример такой задачи.
Пример 4. Требуется найти действительные значения параметра , при которых существуют нетривиальные решения дифференциального уравнения
y y 0 , |
|
(2.32) |
||
удовлетворяющие однородным условиям |
|
|
|
|
y(0) |
|
|
0, |
|
y (0) |
(2.33) |
|||
|
|
|
0. |
|
y(1) |
y (1) |
|
|
|
Решение. Пусть 0 , тогда общее решение уравнения (2.32) будет иметь вид y C1 x C2 . Пытаясь удовлетворить условиям (2.33), получаем
C1 C2 0, C1 C2 0, C1 0,
2C1 C2 0, C2 0, C2 0.
Таким образом, 0 не является собственным значением, так как ему соответствует единственное тривиальное ( y 0 ) решение задачи (2.32), (2.33).
Пусть 0 , тогда y C e x C |
e x , |
|
, и условия (2.33) приводят к |
||||||||||||||||||||||
системе уравнений |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
C |
C |
|
C C |
0, |
|
|
|
|
|
|
(1 |
)C |
(1 )C |
|
0, |
|
|
||||||||
1 |
|
|
2 |
|
1 |
2 |
C2e |
|
0, |
|
|
|
|
1 |
|
|
|
2 |
|
|
0, |
|
|||
C1e |
|
C2e |
C1e |
|
|
|
(1 |
|
)C1e |
|
(1 )C2e |
|
|
||||||||||||
|
|
|
|
|
|
(1 |
)C1 (1 |
)C2 |
0, |
|
(1 |
)C2 0, |
|
|
|
|
|||||||||
|
|
|
|
|
|
)(e |
|
e |
|
)C2 0, |
|
)C1 |
0. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
(1 |
|
|
|
|
(1 |
|
1, C2 0 и |
||||||||||||
Получим |
|
нетривиальное решение |
задачи (2.32), |
(2.33) |
при |
||||||||||||||||||||
собственная функция имеет вид |
|
y e x . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть теперь 0 . Тогда |
y C1 cos( x) C2 sin( x) , |
|
, |
и краевые |
|||||||||||||||||||||
условия (2.33) дают |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
34

C |
C |
|
0, |
|
1 |
|
2 |
C2 sin C1 sin C2 cos 0, |
|
C1 cos |
|
|||
C |
C |
, |
|
|
1 |
2 |
|
sin ) C2 (sin cos ) 0, |
|
C1(cos |
|
|||
C1 |
C2 , |
|
C1 C2 , |
|
C |
(cos sin ) sin cos 0, |
C |
(1 )sin 0. |
|
2 |
|
|
2 |
|
Видим, что существуют нетривиальные решения задачи (2.32), (2.33), если sin 0 , т. е. n , n 1,2,...
Таким образом, множество собственных значений определяется формулойn (n )2 , n 1,2,..., а множество собственных функций, соответствующих собственному значению n , имеет базисную функцию
yn sin( n x)
n x)  n cos(
n cos( n x) sin(n x) n cos(n x).
n x) sin(n x) n cos(n x).
Окончательно получим множество собственных значений и соответствующих им собственных функций:
y1 e x , yn 1 sin( n x)
n x)  n cos(
n cos( n x) sin(n x) n cos(n x),
n x) sin(n x) n cos(n x),
n (n )2 ,n 1,2,...
Для того чтобы убедиться в ортогональности на 0,1 функций yn (x), ym (x) (n m) , достаточно проверить, что
1
( yn , ym ) yn (x) ym (x)dx 0 .
0
V. Пример 4 показывает, что полную систему пробных или поверочных функций ui (x) , i 1 можно составить из последовательно определяемых
нетривиальных решений задачи (2.32), (2.6) трех видов:
u(x) Ae x Be x , 0; |
(2.34) |
|
u(x) Ax B; |
|
(2.35) |
u(x) Acos( x) Bsin( x), |
0. |
(2.36) |
Приведем теперь еще несколько примеров построения пробных решений задачи (2.1) с некоторыми вариантами краевых условий (2.3).
Пример 5. Построить пробное решение (2.7) с краевыми условиями y (0) 2 , y (1) 3.
Решение. |
Пусть u0 Bx Cx 2 . Тогда из граничных условий находим |
B 2 , B 2C |
3 , т. е. B 2 , C 1 2 . Итак, |
u0 (x) 2x 12 x2 .
Построим пробные функции, используя формулы (2.34) – (2.36).
35

Ищем нетривиальное решение вида (2.34). Удовлетворяя однородным
краевым условиям, получаем |
|
|
|
|
|
|
|
|||||
|
A B 0, |
|
|
B A, |
0, |
A 0, B 0, |
||||||
|
|
|
Be |
|
0, |
|
|
e |
|
|||
Ae |
|
|
|
A e |
|
|
|
|||||
следовательно, нетривиального решения нет.
Ищем нетривиальное решение вида (2.35). Из однородных краевых условий, получаем
A 0,
A 0, B 0,A 0,
следовательно, u1(x) 1.
Ищем нетривиальное решение вида (2.36). Из однородных краевых условий, получим
|
|
|
|
|
|
B |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
B 0, |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C R, |
|
|
|
|
|
|
|||||||||||
|
|
|
|
Asin |
Bcos 0, |
|
|
|
A C, |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n N. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n , |
|
|
|
|
|
|
|
||||||
Следовательно, |
имеем |
|
счетное |
множество нетривиальных |
решений |
|||||||||||||||||||||||||||||
uk (x) cos((k 1) x), k 2,3,.... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Таким образом, пробное решение можно искать в виде |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
y |
|
|
|
2x |
1 |
x |
2 |
|
|
|
n |
|
|
|
|
cos((k 1) x) . |
|
|
|
|
|
|
|||||||||
|
|
|
n |
(x) |
2 |
C |
C |
k |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если же функции uk (x) |
( k 1) взять в виде (2.29), то |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
y |
|
|
2x |
1 |
x |
2 |
|
C |
C |
|
|
3 |
|
3 |
x |
2 |
|
n |
|
|
(1 x) |
2 |
x |
k 1 |
, |
|
|||||||
|
n |
(x) |
2 |
|
|
|
x |
|
2 |
|
|
|
C |
k |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
k 3 |
|
|
|
|
|
|
|
|
|||||
если же – в виде (2.30), то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
y |
|
|
2x |
1 |
x |
2 |
|
C |
C |
|
|
3 |
|
3 |
x |
2 |
|
n |
|
|
(1 x) |
k |
1 |
x |
2 |
, |
|
||||||
|
n |
(x) |
2 |
|
|
|
x |
|
2 |
|
|
|
C |
k |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
k 3 |
|
|
|
|
|
|
|
|
|||||
где |
многочлены |
|
P (x) 1, |
P |
(x) x3 3 x2 |
|
|
|
|
удовлетворяют |
|
однородным |
||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P0 (x), P1(x), P2 (x), P3 (x) |
||||||||
граничным условиям и найдены среди многочленов |
|
|||||||||||||||||||||||||||||||||
с неопределенными коэффициентами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример 6. Построить пробное решение для краевой задачи с условиями |
||||||||||||||||||||||||||||||||||
|
2 , y(1) 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y (0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
Методом |
|
|
|
неопределенных |
|
|
|
коэффициентов |
|
находим |
|||||||||||||||||||||||
u0 (x) 2 2x .
Определяя пробные функции из множества (2.34) – (2.36), устанавливаем, что существуют только нетривиальные решения вида (2.36), причем B 0,
A 0, 2k2 1 , k 1,2,3,..., uk (x) cos 2k2 1 x , k N .
Следовательно,
36
|
|
|
|
|
n |
|
2k 1 |
|
|
||||||
|
|
|
|
yn (x) 2 2x Ck |
cos |
|
|
|
|
|
|
x |
. |
||
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
||||
Используя же пробные функции вида (2.29) или (2.30), получаем |
|||||||||||||||
|
|
y |
|
(x) 2 |
|
|
n |
|
|
|
xk (1 |
x) |
|||
|
|
n |
2x C (x2 1) C |
k |
|||||||||||
|
|
|
|
1 |
|
k 2 |
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||
y |
|
(x) 2 |
2x C (x2 1) |
|
|
x2 (1 x)k 1 , |
|||||||||
n |
C |
k |
|||||||||||||
|
|
|
|
1 |
|
k 2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где многочлен P (x) x2 1 удовлетворяет однородным граничным условиям и |
|||||||||
|
|
2 |
|
|
P0 (x), P1(x), P2 (x) |
с неопределенными |
|||
найден |
среди |
многочленов |
|||||||
коэффициентами. |
|
|
|
|
|
|
|||
Пример 7. Построить пробное решение для краевой задачи с условиями |
|||||||||
|
|
|
y(1) 3. |
|
|
|
|
|
|
2y (0) y(0) 1, |
|
|
|
|
|
|
|||
Решение. |
|
Методом |
неопределенных |
коэффициентов |
находим |
||||
u0 (x) 7 |
2 x . |
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
Ищем нетривиальное решение вида (2.34). Удовлетворяя однородным |
|||||||||
краевым условиям, получаем |
|
|
|
|
|
|
|||
|
A B 2 A 2 B 0, |
|
A Be2 , |
|
|
||||
|
|
|
|
|
|
e2 2 e2 2 0. |
|
||
|
Ae |
|
Be 0, |
|
|
B 1 |
|
||
Следовательно, существует нетривиальное решение, только в том случае, если существует отрицательный корень уравнения:
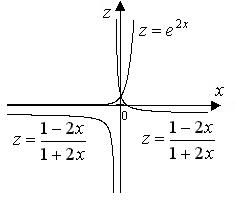
1 2 1 2 e2 . |
(2.37) |
Рисунок 2.1 показывает, что отрицательных корней нет. Получим только тривиальное решение u(x) 0.
Рис. 2.1. Геометрическая иллюстрация корня уравнения (2.37)
Ищем нетривиальное решение вида (2.35). Из однородных краевых условий, получаем
2A B 0, |
|
A 0, |
|
|
A B 0, |
|
|
|
|
B 0, |
|
следовательно, существует только тривиальное решение u(x) 0.
37
Ищем нетривиальное решение вида (2.36). Из однородных краевых условий, получим
2 B A 0,
Acos Bsin 0.
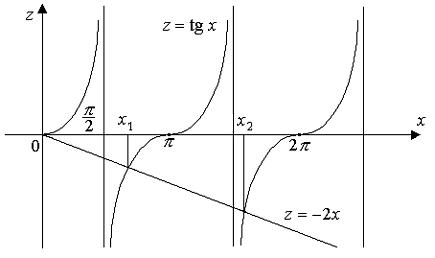
Откуда получаем 2 B A , а значения являются положительными корнями уравнения tg 2 .
Последнее уравнение имеет счетное множество корней 1, 2 , , что
подтверждает рисунок 2.2. Их значения определяются приближенными численными методами, например, метод хорд, метод Ньютона, методом итерации или методом половинного деления. В системе MathCAD корни уравнений отыскиваются с помощью стандартной функции root (см. раздел
6.2).
Рис. 2.2. Геометрическая иллюстрация корней уравнения tgx 2x
Следовательно, |
uk (x) 2 k cos( k x) sin( k x) , |
k 1. |
||||||
|
|
|
|
|||||
Таким образом, пробное решение можно искать в виде |
||||||||
|
yn (x) 7 |
2 x Ck 2 k cos( k x) sin( k x) . |
||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
3 |
3 |
k 1 |
|
|
Если использовать пробные функции вида (2.29), (2.30), то получаем |
||||||||
|
y (x) 7 |
2 x C 3x2 x 2 C xk (1 x) , |
||||||
|
|
|
|
|
|
|
n |
|
или |
|
n |
|
3 |
3 |
1 |
k 2 |
k |
|
|
|
|
|
|
2 x 2 C x2 (1 x)k 1 , |
||
y (x) 7 2 x C 3x |
||||||||
|
|
|
|
|
|
|
n |
|
|
n |
|
|
3 3 |
|
1 |
k 2 k |
|
где многочлен P |
(x) 3x2 x 2 |
удовлетворяет |
однородным граничным |
|||||
|
|
|
2 |
|
|
|
|
|
условиям и найден среди многочленов P0 (x), P1(x), P2 (x) с неопределенными
коэффициентами.
Пример 8. Построить пробное решение для краевой задачи с условиями
|
1, |
|
3. |
y(0) 2y (0) |
y(1) 3y (1) |
38
Решение. Методом неопределенных коэффициентов находим u0 (x) 2 2x .
Определяя пробные функции из множества (2.34) – (2.36), устанавливаем, что существует нетривиальное решение вида (2.34), причем B 0 ,
A |
1 |
2 |
B , а является единственным положительным корнем уравнения |
||||||
1 |
2 |
||||||||
|
|
|
|
2 1 3 1 |
|
||||
|
|
|
e |
2 |
|
|
|||
|
|
|
|
|
. |
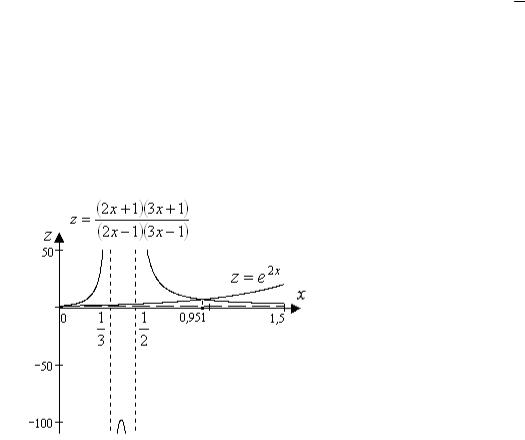
(2.38) |
|||
|
|
|
|
2 1 3 1 |
|||||
Последнее подтверждает рисунок 2.3.
Рис. 2.3. Геометрическая иллюстрация корней уравнения (2.38)
Уравнение (2.38) имеет корень 1 0,951, который может быть найден любым численным методом. Следовательно,
|
x |
|
2 |
1 |
1 |
e |
x |
e |
0.951x |
3,217e |
0.951x |
. |
|
||
u (x) e 1 |
|
|
|
1 |
|
|
|
||||||||
1 |
|
|
2 1 |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Нетривиального решения вида (2.35) не существует. Найдем |
|||||||||||||||
нетривиальные решения вида (2.36): |
A 2 B, B 0 , а значения |
являются |
|||||||||||||
положительными корнями |
уравнения |
tg |
5 |
. |
Таких |
корней это |
|||||||||
1 6 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнение имеет счетное множество 2 , 3 ,..., что подтверждает рисунок 2.4, их значения определяются численным методом.
Следовательно, |
|
|
|
|
|
|
|
|
|
|
||
|
|
uk (x) 2 k cos( k x) sin( k x) , k 2. |
||||||||||
Таким образом, пробное решение можно искать в виде |
||||||||||||
|
x |
|
|
x |
|
2 |
|
1 |
|
|
x |
n |
yn (x) 2 |
|
|
1 |
|
|
|
1 |
|
e |
1 |
|
Ck 2 k cos( k x) sin( k x) . |
|
|
|
|
|||||||||
2 |
C1 e |
|
|
2 1 1 |
|
|
||||||
|
|
|
|
|
|
|
|
k 2 |
||||
Если использовать пробные функции вида (2.29), (2.30), то получаем
y (x) 2 x C |
4x2 5x 10 C |
|
5x3 8x2 C xk 1 |
(1 x)2 |
, |
||
|
|
|
|
|
n |
|
|
n |
|
1 |
|
2 |
k 3 k |
|
|
2 |
|
|
|
||||
или
39

|
y (x) 2 x C 4x2 5x 10 C 5x3 8x2 C x2 |
(1 x)k 1, |
|||||||
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
1 |
2 |
|
k 3 k |
|
|
|
2 |
|
|
|
|||||
где |
многочлены |
P (x) 4x2 5x 10, P (x) 5x3 |
8x2 |
|
удовлетворяют |
||||
|
|
|
|
2 |
|
3 |
|
|
|
однородным |
граничным условиям |
и найдены |
среди |
многочленов |
|||||
P0 (x), P1(x), P2 (x), P3 (x) с неопределенными коэффициентами. |
|
|
|||||||
Рис. 2.4. Геометрическая иллюстрация корней уравнения tg |
|
5 |
|
|||
|
6 2 |
|
||||
|
|
|
1 |
|
||
Пример 9. Построить пробное решение для краевой задачи с условиями |
||||||
|
|
6 . |
|
|
|
|
y(0) 2y (0) 3, |
y(1) y (1) |
|
|
|
|
|
Решение. |
Методом |
неопределенных |
коэффициентов |
находим |
||
u0 (x) x2 x 1.
Определяя пробные функции из множества (2.34) – (2.36), устанавливаем: 1. Не существуют нетривиальные решения вида (2.34);
2. |
|
|
Существуют |
нетривиальные |
решения |
вида |
(2.35), |
причем |
|
A 1 B, B 0 , так что можно взять u (x) x 2 ; |
|
|
|
||||||
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
Существуют |
нетривиальные |
решения |
вида |
(2.36), |
причем |
|
A 2 B, B 0, а значения являются положительными корнями уравнения |
|||||||||
tg( ) |
|
|
|
. |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Последнее уравнение имеет счетное множество таких корней 2 , 3 ,.... Их
значения определяются численными методами. для определения собственных значений.
Таким образом, пробное решение можно искать в виде
n
yn (x) x2 x 1 C1 x 2 Ck 2 k cos( k x) sin( k x) .
k 2
40
