
Ankilov
.pdf
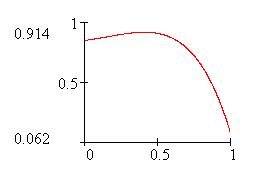
Рис. 6.5. График функции
6.6. Программные блоки
Для решения многих задач в системе Mathcad используются программные блоки. В начале любого блока обязательно должно присутствовать служебное слово Given, далее идет тело блока и в конце стандартная функция, закрывающая блок.
В частности для решения систем алгебраических уравнений линейных или
нелинейных используется программный блок «Given – Find». Например,
Given
a 2b 3c 1 |
|
|
|
|
4a 5b 6c 2 |
|
|
|
|
7a 8b 9c 3 |
|
|
|
|
|
c |
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2c |
|
2 |
|
Find (a, b, c) |
|
|||
|
c |
|
3 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
Здесь телом блока является система уравнений, а с помощью функции Find(x,y,….) получаем искомое решение, где x, y,... есть скалярные переменные, значения которых ищутся в блоке решения уравнений.
171
Приложение. Файл отчета «Иванов_ПМд-31_ODE.doc»
Титульный лист
Лабораторная работа №1 «Решение краевой задачи для линейного обыкновенного
дифференциального уравнения второго порядка»
Выполнил: студент группы ПМд-31 Иванов И.И.
Проверил: преподаватель Сидоров С.С.
172
Описание математической постановки задачи и результаты выполнения подготовительных расчетов
Используя методы Галеркина, Ритца и интегральный метод наименьших квадратов, найти наиболее приближенное к точному аналитическое решение
5 |
(т.е. n 5 ) на отрезке 0,1 для краевой задачи |
|
y5 (x) u0 (x) Ciui (x) |
|
|
i 1 |
|
|
|
y 3y 2 y 2x2 6x 2, |
(А1) |
|
y 0 y 0 1, |
|
|
|
(А2) |
|
|
|
|
y 1 y 1 4 |
|
из пробных решений, построенных: 1) методом Галеркина при помощи системы из 5 пробных функций – многочленов (2.26) и двух систем поверочных функций, одна из которых составлена из пробных функций, а вторая – из многочленов Лежандра (2.31); 2) методом Ритца при помощи двух систем из 5 пробных функций – многочленов (2.26) и функций вида (2.34) – (2.36); 3) интегральным методом наименьших квадратов при помощи двух систем из 5 пробных функций – многочленов (2.26) и многочленов (2.29).
1) Построим функцию u0 (x) для задачи с краевыми условиями (А2). Пусть u0(x) A, тогда u0 0 и условия (А2) дают несовместную систему из
уравнений A 1 и A 4.
Пусть u0 A Bx , тогда u0 B и условия (2.27) дают
|
A B 1, |
A B 0, |
A 6, |
|
|
|
|
B 5, |
|
A 2B 4, |
|
B 5. |
||
Итак, u0 6 5x .
2) Построим систему из пяти пробных функций – многочленов (2.26) для
задачи с однородными краевыми условиями |
0, |
|
y 0 y 0 |
|
|
|
|
(А3) |
|
0. |
|
y 1 y 1 |
|
Определяем u1(x) . Если u1 A или u1 A Bx , то однородные условия (А3) выполняются, если u1 0 , что невозможно из-за требования линейной независимости пробных функций.
Ищем u1 x A Bx Cx2 C 0 , тогда u1 B 2Cx , и из однородных условий (А3) получаем систему
A B 0,
A 2B 3C 0.
Решая ее методом Гаусса, имеем
A B |
0, |
|
|
B 3C 0. |
|
|
||
Видим, что система имеет множество решений
173


Учебное издание
АНКИЛОВ Андрей Владимирович ВЕЛЬМИСОВ Петр Александрович СЕМЁНОВ Алексей Степанович
РЕШЕНИЕ ЛИНЕЙНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ НА ОСНОВЕ МЕТОДОВ ВЗВЕШЕННЫХ НЕВЯЗОК
Учебное пособие
Ответственный за выпуск П.А. Вельмисов
ЛР №020640 от 22.10.97.
Подписано в печать 30.12.2010. Формат 70 100/16.
Усл. печ. л. 14,51. Тираж 500 экз. (1-й з-д 1–100 экз.). Заказ 360.
Ульяновский государственный технический университет 432027, Ульяновск, ул. Северный Венец, 32.
Типография УлГТУ, 432027, Ульяновск, ул. Северный Венец, 32.
180
