Ankilov

б) Задана интенсивность теплового потока через торцевое сечение x a:

(условие Ньютона) означает, что тепловой поток, передаваемый в единицу времени с единицы площади поверхности в окружающую среду, пропорционален разности температур поверхности тела и окружающей среды.

Аналогичные краевые условия могут быть заданы и на правом конце стержня при x b . Например, условие теплообмена при x b имеет вид

Kb y (b) b ( y(b) Tb ).

Втаблице 1.1 приведены возможные варианты краевых условий для

определения стационарного распределения температуры в стержне согласно уравнению (1.7).

Таблица 1.1

Варианты краевых условий для уравнения (1.7)

Напомним еще раз используемые в таблице 1.1 обозначения: Ka K (a), Kb K (b) – коэффициенты теплопроводности;

αа, αb – коэффициенты теплообмена на левом и правом концах стержня

соответственно;

Tа, Tb – температуры, которые поддерживаются на концах стержня при x a и

при x b ;

qа,qb – интенсивности тепловых потоков при x a и при x b .

Очевидно, что все приведенные в таблице 1.1 варианты краевых условий можно записать в виде

11

при соответствующем выборе значений коэффициентов ai , bi . Например, для первого варианта условий из таблицы 1.1 имеем

Таким образом, математическая задача одномерной стационарной теплопроводности формулируется следующим образом: требуется найти функцию y(x) , удовлетворяющую на отрезке a,b обыкновенному линейному

дифференциальному уравнению (1.7), а на концах отрезка – граничным условиям (1.8).

1.3. Постановка начально-краевой задачи нестационарной одномерной теплопроводности

В разделе 1.2 рассмотрена краевая задача для одномерного стационарного уравнения теплопроводности (1.7), которая представляет собой краевую задачу для обыкновенного дифференциального уравнения второго порядка. В случае нестационарной теплопроводности к краевым (граничным) условиям (1.8) добавляется начальное условие в некоторый начальный момент времени t t0

(обычно t 0)

и говорят, что задана начально-краевая задача для уравнения параболического типа (1.4).

1.4. Постановка краевых задач двухмерной стационарной теплопроводности

Согласно (1.6) стационарное (установившееся во времени) распределение теплового поля в пластине описывается уравнением

При решении краевых задач для уравнения эллиптического типа (1.10) наиболее часто используются три типа краевых условий.

а) Краевая задача с граничными условиями первого рода (первая краевая задача).

Требуется найти решение уравнения (1.10) в некоторой области D, принимающее на границе этой области заданные значения. Т. е. нужно найти

12

(применительно к рассматриваемой задаче) стационарное распределение температуры внутри области, если задана температура на границе этой области

Здесь D – граница области D, g(x, y) – известная функция.

б) Краевая задача с граничными условиями второго рода (вторая краевая задача).

Требуется найти решение уравнения (1.10) в некоторой области, на

Если на различных частях границы D заданы условия различного рода, то такие условия и соответствующие им задачи называют смешанными.

1.5. Вывод уравнений поперечных колебаний струны

Рассмотрим тонкую гибкую упругую нить (струну), которая в положении равновесия занимает отрезок a,b оси Ox и концы которой закреплены.

Полагая струну тонкой, пренебрегаем весом струны по сравнению с внутренними силами натяжения и внешней нагрузкой. Полагая струну гибкой, считаем, что внутренние усилия, возникающие в струне, направлены по касательной к мгновенному профилю в каждой точке, т. е. струна не

13

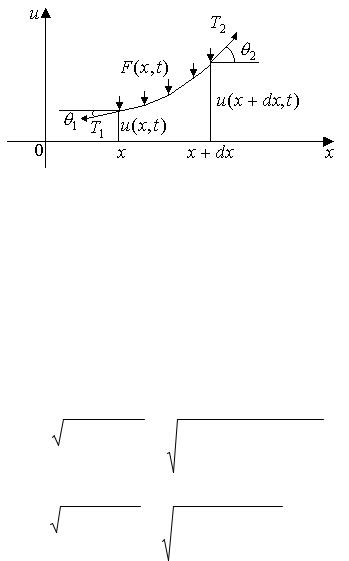
сопротивляется изгибу. Предполагаем также, что внешние силы лежат в вертикальной плоскости, в которой совершают колебания точки струны.

Рассмотрим элемент струны между точками x и x dx (рис. 1.1) и обозначим смещение точек струны через u(x,t) , а длину элемента струны через

ds .

Тогда

откуда, предполагая смещение струны u(x,t) малыми настолько, что

получаем ds dx , т. е. в пределах принятой точности удлинения участков струны в процессе колебаний не происходит. Следовательно, согласно закону Гука величина натяжения в каждой точке струны не меняется со временем и является функцией только x , т. е. T T (x) .

Рис. 1.1. Иллюстрация к выводу уравнения колебаний струны

Запишем условия динамического равновесия элемента струны, на который действуют в плоскости Oxu силы натяжения T1 T (x), T2 T (x dx), внешняя

распределенная по длине дуги с линейной плотностью F(x,t) поперечная сила и сила инерции, направленная вдоль оси Ou .

Так как, согласно тождествам тригонометрии и геометрического смысла производной,

14

то, учитывая условие (1.15), из (1.16) получим T (x dx) T (x) . Откуда, в силу

Теперь, применяя для входящих в формулу (1.17) интегралов теорему о среднем, а для ux (x dx,t) – формулу Тейлора первого порядка с остатком в

форме Пеано, получаем

равенство на dx и осуществляя предельный переход при dx 0 , получаем уравнение колебания струны следующего вида:

Q(x,t, ) – ядро релаксации, учитывающее изменение с течением времени физико-механических свойств материала основания (т. е. его старение).

15

Заметим, что при выводе уравнения (1.19) предполагалось, что реакция основания пропорциональна его деформации (модель Винклера).

В статических задачах профиль струны u u(x) определяется, согласно

0, то получаем закон Гука для упругого тела.

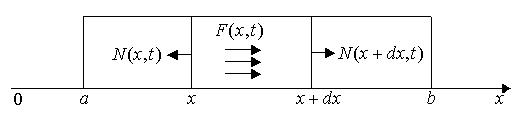
Рассмотрим элемент стержня (рис. 1.2), заключенный между поперечным сечением с координатами x и x dx .

Рис. 1.2 Иллюстрация к выводу уравнения продольных колебаний стержня

В сечении « x » на элемент действует сила N (x,t) (x,t)S(x), где S(x) – площадь сечения, в сечении « x dx » – сила N (x dx,t) (x dx,t)S(x dx)) .

Предполагая, что на стержень действует внешняя нагрузка, распределенная по длине стержня с объемной плоскостью F(x,t) , аналогично выводу уравнения

(1.18) получаем уравнение продольных колебаний стержня следующего вида:

где (x) – объемная плотность материала стержня; u(x,t) – продольное

смещение сечения стержня с координатой x в момент времени t от положения, которое занимало это сечение, когда стержень находился в ненапряженном состоянии.

16

Если боковая поверхность стержня скреплена с вязкоупругим основанием (модель Винклера), то приходим к следующему уравнению:

где (x,t), (x,t) – коэффициенты жесткости и демпфирования основания; Q(x,t, ) – ядро релаксации основания. Заметим, что форма записи уравнения (1.23) не изменится, если считать S и зависящими от времени t .

Статические продольные смещения u(x) сечений стержня определяются, согласно (1.23), решением уравнения

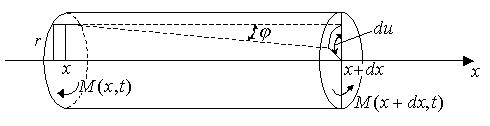
Для вязкоупругого стержня, находящегося в состоянии кручения (рис. 1.3), связь между напряжением , вызванным сдвигом образующей на угол , и

этим углом может быть представлена формулой

Рис.1.3. Иллюстрация к выводу уравнения крутильных колебаний стержня

17

Крутящий момент M (x,t) , действующий в сечении S стержня, соответствующем координате x , определяется формулой

M (x,t) r ds .

S

Отсюда, используя выражения (1.25), (1.26), получаем

где J0 r 2dS – полярный момент инерции сечения.

S

Рассмотрим элемент стержня, заключенный между поперечными сечениями с координатами x и x dx (рис. 1.3). В сечении « x » действует крутящий момент M (x,t) , в сечении « x dx » – M (x dx,t) . Предполагая, что

на стержень действует крутящий момент внешних сил, распределенный по длине стержня с линейной плотностью F(x,t) , из уравнения динамического

равновесия получаем

( 1 )J0 ( 1 ) 2u(t 21,t) M (xx,t) dx o(dx) F( 2 ,t)dx,

где – плотность стержня; 1 и 2 – принадлежат x, x dx . Откуда

аналогично уравнению (1.18) получаем уравнение крутильных колебаний стержня

(x,t)J0 (x) 2u(x,t) F(x,t).

Если боковая поверхность стержня скреплена с вязкоупругим основанием (модель Винклера), то для описания крутильных колебаний приходим к уравнению

(x,t) u(x,t) F(x,t),

t

где , ,Q – коэффициенты жесткости, демпфирования и ядро релаксации основания.

18

Заметим, что форма записи уравнения (1.27) не изменится, если считать и J0 функциями двух переменных x и t .

Статические углы поворота u(x) сечений стержня при кручении определяются, согласно (1.28), решением уравнения

1.7.Постановка статических краевых задач для струны и стержня

Встатическом варианте профиль струны, продольные и угловые перемещения сечений стержня, согласно (1.20), (1.24) и (1.29), определяется решением уравнения

где y(x) u(x); a x b ;

K (x) T0 , g(x) F(x), если рассматривается задача (1.20);

K (x) S(x)E(x), g(x) S(x)F(x), если – задача (1.24);

K (x) J0 (x)G(x), g(x) F(x), если – задача (1.29).

Перечислим основные типы граничных условий при x a для уравнений

(1.20), (1.24), (1.29) в обозначениях уравнения (1.30).

а) y(a) 0; это условие соответствует жесткому закреплению левого конца

струны и стержня.

б) K (a) y (a) qa ; это условие соответствует заданию на левом конце стержня продольной силы N(a) qa для задачи (1.24) и заданию крутящего момента M (a) qa в случае задачи (1.29). В частности, если левый конец свободен, то qa 0.

в) K(a) y (a) a y(a) ; это условие соответствует упругому закреплению левого конца стержня, когда qa a y(a) ( qa или равно N(a), или – M (a) ), гдеa – соответствующий задаче (1.24) или (1.29) коэффициент закрепления.

Аналогичные краевые условия могут быть заданы и на правом конце струны или стержня при x b . Очевидно, что все возможные варианты краевых условий для уравнения (1.30) можно получить из условий (1.8) при соответствующем выборе значений коэффициентов ai ,bi .

Таким образом, рассматриваемые статические краевые задачи для струны и стержня математически формулируется так же, как и задача стационарной теплопроводности из раздела 1.2.

1.8. Краевые задачи в теории колебаний струн и стержней

Предположим, что геометрические и прочностные характеристики упругих тел (струны, стержня) и оснований, на которые они опираются, зависят только от x , и запишем уравнения движения без учета демпфирования и старения.

19

Уравнения (1.31)–(1.33) являются уравнениями гиперболического типа. Рассмотрим гармонические колебания упругих тел. В этом случае решение

уравнений (1.31)–(1.33) и приложенную внешнюю нагрузку F(x,t) представим в виде:

* (x) (x) (x) 2 соответствует уравнению (1.31),

* (x) (x) (x)S(x) 2 – уравнению (1.32),

* (x) (x) (x)J0 (x) 2 – уравнению (1.33).

Приведем основные типы граничных условий при x a .

а) u(x,t) a (t); это условие соответствует движению левого конца струны или стержня по закону a (t) .

б) K (a) u(a,t) qa (t); это условие соответствует заданию на левом конце

x

стержня продольной силы N (a,t) qa (t) для задачи (1.32) и заданию крутящего момента M (a,t) qa (t) в случае задачи (1.33). В частности, если левый конец свободен, то qa 0 .

закреплению левого сечения стержня, движущегося (вращающегося) по закону

a (t) .

Предполагая функции a (t), a (t),qa (t) периодическими во времени,

где a0 , a0 ,qa0 – постоянные. Тогда для u* (x) y(x) будем иметь граничные условия следующего вида:

а) y(a) a0 ;

20