Уравнение Пфаффа.

Наша задача:1)нахождение векторной линии2)нахождение векторного пространства. Не редко возникает и3)задача связанная с этим же векторным полем-нахождение семейства поверхностей ,которые ортогональны векторному полю.,то уравнения искомых поверхностей, как условие ортогональности векторов:(F,dt)=0 P(x,y,z)dx+Q(x,y,z)dy+ +R(x,y,z)dz=0(1). (1)-условие ортогональности линий к векторному полю, оно наз. ур-ем Пфаффа.(1) определяет поверхности в трех мерном пространстве, которые в каждой точке ортогональны векторному полю F. Уравнение Пфаффа-необыкновенное урав-е. Любое обыкн-е диф. ур-е имеет бесконечно много частных решений. Некоторые ур-я Пфаффа имеют бесконечно много реш-ий, то задача 1), а попутно задача 2). 1 ситуация: урав. Пфаффа имеет реш-е: поле F является потенциальным .Опр1:Векторное поленаз.потенциальным, если существует скалярная функция,градиент которой совпадает с полемF т.е. F=grad,Если,то оно может быть найдено с помощью крив. интеграла:Значение этого крив. интеграла не зависит от выбора пути интегрирования. Рисунок.

Функция Uназ.потенциалом F- векторного поля. du=Pdx+Qdy+ +Rdz=0 В силу (1) U=C.Если F потенц., то компоненты связаны потенциалом этого поля (U) уравнения (2).Продиф. (2): rot F-диф.оператор прилож. к векторному полю.

-необходимое и достаточное условие. Рисунок.

Самый простой путь-ломанная т.к.пользуясь св-ом единственности крив. интеграла наш интеграл разбивается на сумму 3-х интегралов. 2 ситуация: ПустьF не явл. потенциальным, то иногда удается подобрать скалярную функцию М(x,y,z) ,после умножения на которую MF-потенциальное поле. Если такая сущ-ет, то интегрирующий множитель ур. Пфаффа. Выясним условие сущ-я интегрирующего множителя: пусть он сущ-ет, то MF-потенциальное т.е. илиПрименим кMF условие потенциальностине модульиз1)/*R из 2) /*P из 3) /*Q(4)-условие полной интегрируемости ур.Пфаффа необходимое и достаточное для сущ-ия поля поверхностей. -необходимо. Докажем достаточность.Опр: вихревой линией поля F наз. векторная линия поля rotF т.е. линия касательная к которой в каждой точке параллельно полю rotF в этой же точке. Опр. Вихревой поверхностью F наз. векторная поверхность поля rotF т.е. поверхность составленная из вихревых линий. Пусть (4) выполнено. Докажем, что в этом случае сущ. поверхности ортогональныеF. В каждой точке поверхности определяемой (5) уравн. (1) Pdx+Qdy+ +Rdzдолжно обращаться в тождество или

рисунок.

S-произвольная вихревая поверхность поля F. C-замкнутый контур. Д-поверхность огран. контуром. dt-вектор бесконечно малой касательной в точке. n-вектор нормали к С.

Т. Стокса: справедлива для любого векторного поля. S-вихревая поверхность. rotF в каждой точке поверхности S ортогонелен, n. Т.об. для любой вихревой поверхности и замкнутого контура на ней крив. интеграл вида Выберем и из всех вихревых поверхностейF те которые ортогональны полю F. Для того, чтобы построить вихревую поверхность: 1) выбираем в пространстве произвольную проведем через А кривую ортогональную полюF. Одно из них уровнение Пфаффа. Pdx+Qdy+ +Rdz=0 вторую поверхность выбираем произвольно через А: Z=f(x,y) Z=f(x) Z=f(y) Z=a Pdx+Qdy+ +Rdz=0 Z=f(x,y) Подставим Z в предпоследнее уравнение получим M(x,y) dx+N(x,y)dy=0 (6) (7) – уравнение первого порядка в симметричной формеZ=f(x,y) рис.

l эта кривая ортогональна полю F по построению. Если l не является вихревой линией поля F, то проводя через каждую точку l вихревую линию поля F получим вихревую поверхность. если же l является вихревой поля F, то через нее можно провести бесконечно много вихревых поверхностей. Она не подходит. Выберем уравнение поверхности Z=f(x,y) и все аналогично, пока l не окажется вихревой. Докажем что S является искомой в каждой точке ортогонально полю F. Выберем L. Через Е1, Е2 проводим вихревую линию и они пересекутся с l в В1, В2 то, появлется замкнутый контур С. .То S обладает нужным свойством,то достаточность 4) доказана.

1) Уравнения с разделяющимися переменными и приводящиеся к ним.. Опр. 1Уравнением с разделяющимися переменными называется дифференциальное уравнение, которое может быть представлено в виде:y^/=f(x)g(y) или в видеf(x)g(y)dx+h(x)p(y)dy=0 (0). Для нахождения общего решения этого уравнения с разделяющимися переменными нужно разделить переменные, т. е. путем деления обеих частей уравнения на произведениеg(y)h(x) добиться того, чтобы в преобразованном уравнении коэффициент приdxявлялся бы функцией только от переменнойx, а коэффициент приdy– функцией только от переменнойy:.Опр. 2Уравнение этого вида называется дифференциальным уравнением с разделенными переменными. Интегрируя, найдем общий интеграл. В общем случае (0) и (1) неэквивалентны, т.е. у них не одинаковы множества решений. Связано это с тем, что деление наg(y)h(x) может привести к потере некоторых частных решений (0), обращающихся в нуль произведениеg(y)h(x). Поэтому вконкретном случае необходимо:1)необходимо находить все решения уравненияg(y)h(x)=0. Эти функции будем называть подозрительными; 2)из подозрительных функций необходимо по отдельности проверить, не явл-ся ли она решением (0). Та из них, которая явл-ся решением (0) наз-ся потерянным решением, т.к. эта функция явл-ся решением (0), но не явл-ся решением (1). После того как оба интеграла в (2) вычислены, получим конечное уравнение, связывающее х и у, в котором нет ни производных, ни дифференциалов.. Из этого уравнения можно выразитьпеременную, либо х , либо у ч/з другую, т.е. получить решение уравнения в явной форме, но это удается не всегда. В случае, если уравнение (2) невозможно решить относительно у или х , мы все равно считаем уравнение (1) решенным, но решение получено в неявной форме.Опр 3. Конечное уравнение виданаз-ся частным интегралом (1) или частным решением в неявной форме, если при подстановки некоторого (одного) частного решения (1) уравнение (3) обращается в истинное тождество.Опр. 4Конечное уравнение видас произвольной постоянной С наз-ся общим интегралом уравнения (1), если при подстановкичастного решения (1) при каком-либо значении С уравнение (4) обращается в истинное тождество.Замеч-ие.Определения (3) и (4) справедливы дляуравнения первого порядка. Уравнение, правая часть которого является функцией линейного аргумента:y^/=f(ax+by+c), гдеaиb– постоянные, сводится к уравнению с разделяющимися переменными с помощью замены исходной переменнойz=ax+by+c. Вычисляя производную от новой искомой функцииz^/=a+by^/и используя исходное уравнение, получаем:z^/=a+bf(z), откуда. Интегрируя, получим общий интеграл:, в котором осталось сделать обратную замену переменнойz=ax+by+c.

2) Однородные дифференциальные уравнения первого порядка и приводящиеся к ним. Однородным называется уравнение, которое может быть представлено в виде:y^/=f(y/x) или:M(x,y)dx+N(x,y)dy=0, гдеM(x,y) иN(x,y) – однородные функции одинаковой степени однородности. ФункцияF(x,y) называется однородной степениn, если для любогоt>0 выполняется тождество:F(tx,ty)≡tⁿF(x,y). Однородное уравнение сводится к уравнению с разделяющимися переменными с помощью замены искомой переменнойz=y/xилиy=xz. Дифференцируя указанную замену поx, получаемy^/=xz^/+zдля первой формы однородного уравнения иdy=xdz+zdxдля второй. Подставляя найденную производную в исходное уравнение, получаем уравнение с разделяющимися переменными:xz^/+z=f(z), или. Интегрируя, получаем общий интеграл:, в котором осталось сделать обратную замену переменнойz=y/x. Уравнение с правой частью в виде функции дробно-линейного аргумента, гдеa₁,b₁,c₁,a₂,b_2,c₂– постоянные, преобразуется в однородное уравнение с помощью введения новых переменныхuиvпо формуламx=u+x₀,y=v+y₀(1), гдеx₀иy₀– решение системы линейных алгебраических уравненийa₁x+b₁y+c₁=0,a₂x+b₂y+c₂=0. Так как, то, подставляя (1) в исходное уравнение, получаем, то есть получаем однородное уравнение вида. Описанный метод неприменим в случае параллельности прямых (2). Но в этом случае коэффициенты в уравнениях (2) пропорциональныa₂/a₁=b₂/b₁=k, и исходное уравнение можно записать в виде, и заменой переменнойz=a₁x+b₁yсвести к уравнению с разделяющимися переменными.

3) Линейные дифференциальные уравнения первого порядка. Метод вариации постоянной. Линейным дифференциальным уравнением первого порядка называется уравне- ние линейное относительно неизвестной функции и ее производной. Линейное уравнение имеет вид:y^/+p(x)y=f(x) (1). Еслиf(x)≡0, то уравнение (1) называется линейным однородным. Для интегрирования неоднородного линейного уравнения применяется метод вариации постоянной, который состоит в следующем. Сначала интегрируется соответствующее однородное линейное уравнениеy^/+p(x)dx, в котором переменные разделяются:, откуда, интегрируя, получаем, где С – произвольная постоянная. Решение исходного уравнения ищем в виде(2), где С(х) – новая неизвестная функция переменной х. Вычислим производнуюdy/dx:. Подставим ее и (2) в исходное уравнение (1):, после приведения подобных получаем, откуда, интегрируя, находим функциюи после ее подстановки в (2) получаем общее решение исходного уравнения:, где первое слагаемое – решение однородного уравнения, а второе слагаемое – частное решение. Т.о. решение линейного уравнения = решение соответствующего однородного уравнения (общего) +некоторое частное решение неоднородного уравнения (1).

4) Уравнения Бернулли и Риккати. Уравнение видаy^/+p(x)y=f(x)yⁿ,n≠1 (1) наз-ся уравнениемБернулли.2 способа решения данного уравнения:1) заменой переменнойz=y^1-nсводится к линейному уравнению. Умножим обе части (1) наy^-n(1-n), получим(2). Сделав заменуz=y^1-nи подставив в (2), получим- линейное уравнение. 2) методом вариации постоянной. Сначала интегрируем соответствующее однородное уравнениеy^/+p(x)y=0, в котором переменные разделяются:, откуда, интегрируя, получаем, где С – произвольная постоянная. Решение исходного неоднородного уравнения Бернулли ищем в виде(3), где С(х) – новая неизвестная функция переменной х. Вычисляя производнуюdy/dxи подставляя ее и (3) в исходное уравнение, после приведения подобных получаем- уравнение с разделяющимися переменными относительно неизвестной функции С(х), интегрируя которое, находим С(х) и после подстановки в (3) получаем общее решение исходного уравнения. Уравнение, имеющее видy^/+p(x)y+q(x)y²=f(x) наз-ся уравнениемРиккати. Если известно одно частное решениеu(x) этого уравнения, то оно заменойy=u+z, гдеz(x) – новая неизвестная функция, сводится к уравнению Бернулли. Действительно, подставляя указанную замену в исходное уравнение, получимu^/+z^/+p(x)(u+z)+q(x)(u+z)²=f(x)или, учитывая, чтоu^/+p(x)u+q(x)u²≡f(x), после приведения подобных будем иметь уравнение Бернулли:z^/+(p(x)+2q(x)u(x))z= -q(x)z².

5) Уравнения в полных дифференциалах. Интегрирующий множитель. Уравнение, записанное в симметричной формеM(x,y)dx+N(x,y)dy=0 (1), называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функцииu(x,y) двух независимых переменных (она наз-ся потенциальной функцией уравнения (1)), то есть.du(x,y)=0, т.к. левая часть совпадает с правой частью (1). Предположим, что у = у(х) явл-ся решением (1). Тогдаdu(x,y(х))≡0u(x,y)=С (2), где С – произвольная постоянная. Т.о. мы получили конечное уравнение (2), определяющее все частные решения (1), но в неявной форме или получили общий интеграл уравнения (1). Для того чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие Эйлера:(3). Д-во.1)Необходимость. Предположим, что потенциальная функция уравнения (1) существует. Покажем, что в этом случае будет справедливо условие (3).. Т.к. в правых частях обеих последних формул дифференциалыdx,dyменяются независимо друг от друга, то совпадение правых частей возможнокогда коэффициенты при них совпадают, т.е.. Продифференцировав первое равенство (4) по у, а второе по х, получим. Достаточность. Предположим, что справедливо условие (3) . В этом случае гарантируется существование потенциальной функции. Для нахождения функцииu(x,y) воспользуемся условием (4). Если потенциальная функция существует, то она должна удовлетворять (4) Интегрируя первое из равенств (4) по х (считаяyпостоянной), имеем(5), где φ(y) – произвольная функция отy. Дифференцируя полученное выражение поyи подставляя во второе из равенств (4), получаем. Последнее уравнение имеет смысл, а стало быть и решениеправая часть от х не зависит, а правая часть в силу условия Эйлера не зависит от х. Поэтому, интегрируя его поy, находим, подставляя результат в (5), получим искомую функцию. Вычислим от правой части (6) частную производную по х:. Т.к. правая часть (6) от х не зависит, значит достаточность доказана. Существует второй способ построения потенциальной функции:. Теорема. Криволинейный интеграл (7) при выполнении (3) не зависти от выбора пути интегрирования. Самой простой кривой, вдоль которой можно вычислить интеграл явл-ся ломаная, соединяющая наши 2 точки со звеньями, параллельными осям координат.В некоторых случаях, когда уравнение (1) не является уравнением в полных дифференциалах, удается подобрать функциюпосле умножения на которую левая часть уравнения (1) превращает в полный дифференциал. Такая функцияназывается интегрирующим множителем. Из определения интегрирующего множителя следует и условия Эйлера, следует что он должен удовлетворять уравнению, илиили(8). В общем случае задача интегрирования этого уравнения в частных производных не легче, чем задача интегрирования уравнения (1), однако в некоторых частных случаях это уравнение упрощается и интегрирующий множитель μ легко находится. 1. Уравнение (1) имеет интегрирующий множитель, зависящий только от х. В этом случае уравнение (8) принимает вид. В этом уравнении левая часть является функцией только отx. Значит и правая часть должна быть функцией только от х, в противном случае интегрирующего множителя вида μ=μ(х) не существует. 2. Уравнение (1) имеет интегрирующий множитель, зависящий только отy. В этом случае уравнение (8) принимает вид. В этом уравнении левая часть является функцией только отy. Значит и правая часть должна быть функцией только отy, в противном случае интегрирующего множителя вида μ=μ(y) не существует. 3. Уравнение (1) имеет интегрирующий множитель μ=μ(z(x,y)), гдеz(x,y) – известная функция. В этом случае уравнение (8) принимает вид. 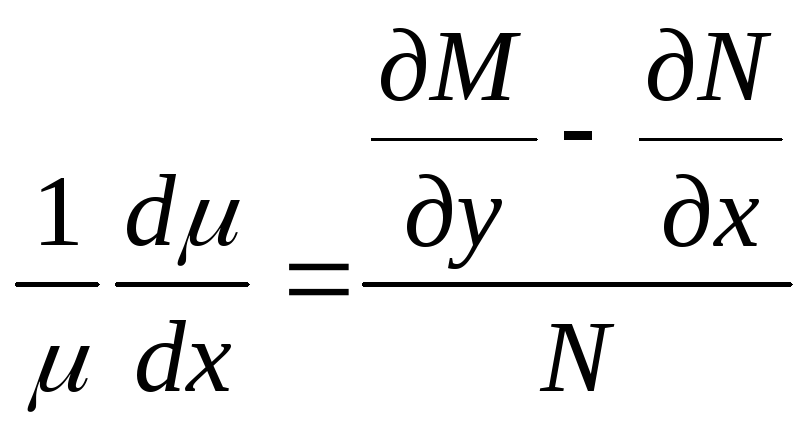В этом уравнении левая часть является функцией только отz. Значит и правая часть должна быть функцией только отz, в противном случае интегрирующего множителя вида μ=μ(z) не существует.

***********************************************************************************

7) Дифференциальные уравнения, не разрешенные относительно производной. Опр. 1 Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет видF(x, у, у')=0 (1). В некоторых случаях (1) можно разренить относительно производной .Если это возможно, то получается одно либо несколько уравнений, уже разрешенных относительно производной: у' =f_i(х, у), гдеI= 1,2,…,каждое из которых решается отдельно подходящим методом интегрирования уравнения, разрешенного относительно производной. Объединяя решение каждого из этих уравнений, мы получим общее решение данного уравнения. Уравнение (1) разрешается относительно производной крайне редко. Даже если (1) можно разрешить относительно производной, то в результате такого разрешения можно получить настолько сложное уравнение, которое не удастся проинтегрировать.Опр. 2.Частным решением (1) в параметрической форме наз-ся 2 функции х иу, зависящие отt: , которые при подстановки в (1) обращают его в истинное тождество. При подстановке в (1) мы должны подставлять не только х у, но и у', т.е. .Опр. 3Общим решением (1) в параметрической форме наз-ся совокупность всех его частных решений без исключения.Опр. 4 Если левая часть уравнения (1) не содержит независимой переменной х или искомой функции у, или того и другого вместе, то оно называется неполным. Рассмотрим некоторые из частных случаев.1.Простейшим из неполных уравнений является уравнение, содержащее только производную:F(y') = 0. Общий интеграл такого уравнения находится следующим образом. Предположим, что это уравнение имеет некоторое (конечное или бесконечное) число вещественных корнейy'=k_i, (i=l, 2, ...) (2), гдеk_i- некоторые постоянные, так что имеют место тождества:F(k_i)=0, (i=1,2,…) (3). Интегрируя уравнения (2), находим у =k_ix+С, откуда . После подстановки этого значенияk_iв тождество (3) приходим к одному соотношению. Это соотношение и есть общий интеграл исходного уравнения.2.Уравнение видаF(x, у')=0, не разрешенное относительно производной и не содержащее искомой функции, интегрируется методом введения параметраtи заменой исходного уравнения двумя уравнениями:x=φ(t),y^/=ψ(t). Для того, чтобы найти у через параметрt, воспользуемся основным тождеством диф. исчисления, который устанавливает связь м/у дифференциалом функции и ее производной. dy=y'dx, то в данном случае, откудаи, следовательно, общее решение исходного уравнения в параметрической форме определяется следующими уравнениями:,.2а).Если исходное уравнение легко разрешимо относительно х: то удобно в качестве параметра ввести у' =t. Тогда,,.3.Уравнение видаF(y,y')=0, не разрешенное относительно производной и не содержащее независи­мой переменной, также интегрируется методом введения параметраtи заменой исходного уравнения двумя уравнениями:,. Так какdy=y'dx, то в данном случае, откудаи, следовательно, общее решение исходного уравнения в параметриче­ской форме определяется следующими уравнениями:,.3а).Если исходное уравнение легко разрешимо относительно у:, то удобно в качестве параметра ввестиy'=t. Тогда,,.4.Если уравнениеf(z, у, у')=0 разрешимо относительно искомой функции, то есть приводится к видуy=f(x,у'), то, считая х и р = у' параметрами, получаем следующее пapaметрическое представление исходного уравнения:y=f(x,p),y^/=p. Для нахождения общего решения уравненияy=f(x,у') мы воспользуемся методом интегрирования с помощью дифференцирования. Продифференцируем обе части по х:то, учитывая, что у' = р, получаем уравнение, разрешенное относительно производной:. Интегрируя полученное уравнение (если оно интегрируется в квадратурах), получим Ф(х, р, С)=0. Совокупность уравнений Ф(х, р, С)=0,y=f(x,p) является общим решением исходного уравнения в параметрической форме.5.Если уравнениеF(x, у, у')=0 разрешимо относительно независимой переменной:x=f(y,y^/), то, считая у и р=у' параметрами, получаем следующее параметр кое представление исходного уравнения:x=f(y,p),y'=р. Воспользуемся методом интегрирования с помощью дифференцирования. Продифференцируем обе части по у:, и, учитывая, что у'=р, получаем уравнение, разрешимое относительно производной:. Интегрируя полученное уравнение (если оно интегрируется квадратурах), получим Ф{у, р, С)=0. Совокупность уравнений Ф(y,p,С)=0,x=f(y, р) является общим решением исходного уравнения в параметрической форме.

8) Уравнения Лагранжа и Клеро. Опр. 1 УравнениемЛагранжаназывается линейное относительно х, у уравнение. Для интегрирования этого уравнения вводим параметр р = у'. Тогда(1). Дифференцируя по переменной х и полагая у'=р, получим, или. Это линейное относительно х иуравнение легко интегрируется, например, методом вариации постоянной. Найдя его общее решение х=χ(р,С) и присоединяя к нему соотношение (1), получаем общее решение ис­ходного уравнения в параметрической форме: х=χ(р,С) (2),. В процессе решения при делении намогут быть потеряны решения, при этом от (1) останетсяp=φ(p). Если оно имеет действительные корни р = р_i(i=l,2,…), то к ранее найденным решениям (2) и (3) можно добавить потерянное решение у = хφ(p_i)+ψ(p_i). Рассмотрим ситуацию, когда.Опр. 2УравнениемКлероназывается частный случай уравнения Лагранжа: у = ху'+ψ(у^/). Для интегрирования этого уравнения вводим параметр р = у'. Тогдаy=xp+ψ(p) (4). Воспользуемся метод интегрирования с помощью дифференцирования. Дифференцируя по переменной х и полагая у'=р, получим, или. Откудаили. В первом случае р=С и, исключая р из (4), получим:y=Cx+ψ(C) (5) - однопараметрическое семейство интегральных прямых. Во втором случае решение определяется двумя уравнениямиx=-ψ^/(p),y=-pψ^/(p)+ψ(p) (6) в параметрической форме. Последние 2 уравнения явл-ся частным решением. Интегральная кривая, определяемая уравнениями (6) является огибающей семейства интегральных прямых (5).Опр. 3Огибающей семейства кривых на плоскости, заданных уравнением Ф(х, у, С)=0 (7) наз-ся кривая , имеющая в каждой своей точке общую касательную с одной из кривых семейства. Уравнениеопределяет огибающую семейства (7), а уравнениеопределяет огибающую к (5).

9) Теорема существования и единственности решения дифференциального уравнения первого порядка, не разрешенного относительно производной. Особые решения. Рассмотрим диф. уравнениеF(x,y,y') =0 (1);y(x₀) =y₀ (2) – начальное условие. Для уравнения (1) встает вопрос о единственности решения этого уравнения, удовлетворяющему условию (2). Понятие единственности решения этого уравнения понимается не так как для решения, разрешенного относительно производной (уравненияy' =f(x,y)). Уравнение (1) в принципе можно разрешить относительноy'.,i= 1, 2,… Если каждое из уравнений вида (3) удовлетворяет условию (2), то ч/з каждую точку (x_0, y₀) будет проходить только одна интегральная кривая уравнения (3). Под единственностью решения уравнения (1) мы будем понимать, что ч/з заданную точку (x_0, y₀) проходит одна интегральная кривая в заданном направлении.Теорема. Если в уравненииF(x,y,y') = 0 в некоторой замкнутой окрестности точки (x₀,y₀,y₀'), гдеy₀' – один из действительных корней уравненияF(x_0, y₀,y₀') = 0, функцияFудовлетворяет условиям:1)F(x,y,y') непрерывна по всем аргументам; 2); 3), то на отрезкеx₀-h≤x≤x₀+h, гдеhдостаточно мало,единственное решениеy=y(x) уравнения (1) удовлетворяющее начальному условию (2), для которогоy'(x₀) =y₀'. Д-во. Из курса анализа по теореме о неявной функции выполнение первых двух условий нашей теоремы гарантирует существование единственной неявной функцииy' =f(x,y)) (4);y'(x₀) =f(x₀,y₀), при этом функцияf(x) будет непрерывна. При выполнении всех трех условий нашей теоремы у функцииf(x) будетогранич. частн. производная по переменной у. Для того, чтобы а этом убедиться, воспользуемся теоремой о дифференцировании неявной функции, в которой при выполнении условий 1), 2), 3) гарантируетсячастной производнойот нашей новой функции и она может быть найдена по правилу дифференцирования неявной функции.F(x,y,y') = 0. Продифференцируем обе части по у:. Т.о. второе условие теоремы ои единственности решения диф. уравнения, разрешенного относительно производной для уравнения (4) выполненоединственное решение (4), удовлетворяющее начальному условию (1)единственное решение (1).Особые решения. Опр.1 Точки на плоскости хОу, в которых нарушается свойство единственности уравнения (1) называются особым множеством уравнения (1).В точках этого множества должно нарушаться хотя бы одно из условий теоремы. В уравнениях, которые встречаются на практике условия 1), 3) нашей теоремы обычно выполняются , условие 2), гдечасто нарушается, Если 2) и 3) выполнены, то в точках особого множества должно выполняться:F(x,y,y') =0 и. Если из них исключитьy', то мы получим, которому ложны удовлетворять точки особого множества.Опр. 2Кривая на плоскости хОу, определяемая уравнением (5) наз-ся дискреминантной кривой уравнения (1). Не все точки дискр. кривой будут принадлежать особому множеству уравнения (1) , т.к. условия нашей теоремы явл-ся достаточными для единст-ти, но не явл-ся необходимыми, т.е. нарушение какого-либо из условий теоремы не обязательно влечет нарушение единственности решения.Опр. 3Если какая-либо ветвь дискр. кривой (5)явл-ся интегральной кривой уравнения (1) или графиком одного из частных решений и при этом принадлежит особому множеству ур-я (1), то эта интегр. Кривая наз-ся особой интегральной кривой уравнения (1), а функцияназ-ся особым решением уравнения (1). Т.о. для того, чтобы найти особое решение уравнения (1), необходимо:1)найти дискримин. кривую уравнения (1); 2)для каждой из ветвей дискримин. кривой проверить, является ли она интегр. кривой уравнения (1); 3)проверить нарушается ли в точках этой интегр. кривой единственность решения ур-я (1).

26) Однородные системы линейных дифференциальных уравнений. Основные свойства решений. Опр. 1 Система дифференциальных уравнений называется линейной, если она линейна относительно искомых функций х_i(t) и их производных. Линейная системаn-го порядка, имеет вид, где а_ij(t) (i,j=1,2,…,n) в количествеn²штук наз-ся коэффициентами системы (1),f_i(t) (nштук) наз-ся правыми частями системы (1). Пусть,,,. Тогда в краткой векторной форме система (1) может быть записана в следующем виде. Если все коэффициенты а_ij(t), правые частиf_i(t) системы (1) явл-ся непрерывными на отрезке, то система (1) на этом же отрезке удовлетворяет условиям теоремы о сущ-нии и един-ти решения. Дейст-но полные правые части системы (1)будут непрерывны по всем своим аргументам, т.к. они явл-ся линейными комбинациями. Существуют ограниченные частные производные от правых частей. Эти функции непрерывны, по т.Вейштрасса ограничены.Опр. 2Если в системе уравнений (1) все правые частиf_i(t)≡0 (i,j=1,2,…,n) илиF(t)=0, то система (1) наз-ся линейной однородной. Линейная однородная системаn-го порядка имеет видили.Основные свойства частных решений:1)Если Х(t) явл-ся решением лин. однородной системы (2), то СХ(t),C=constтакже явл-ся решением (2). Д-во.; 2)Если 2 векторные функции Х₁(t), Х₂(t) явл-ся решением одной и той же системы (2), то Х₁(t)+Х₂(t) тоже явл-ся решением (2). Д-во.; 3) Если Х₁(t), Х₂(t),…,Х_m(t) явл-ся решением одной и той же системы (2), то линейная комбинация от этих функций сconstявл-ся решением одной и той жеcистемы.4)Если лин. однородная система (2) с действительными коэффициентами а_ij(t) имеет комплекснозначное частное решениеX(t)=U(t)+iV(t), то вещественные и мнимые части этого решения по отдельности также явл-ся решением (2), Д-во.; При подстановки должны получить тождество:. Две комплекснозначные функции тождественно совпадаюту них совпадают тождественно вещественные и мнимые части.

27) Определитель Вронского линейной однородной системы уравнений и его основные свойства. Опр. 1 Х₁(t), Х₂(t),…,Х_n(t) наз-ся линейно зависимыми на отрезке, еслии длявыполняется.Опр. 2Х₁(t), Х₂(t),…,Х_n(t) наз-ся линейно независимыми на отрезке, если для них тождество (1) выполняется, когда.Опр. 3Х₁(t), Х₂(t),…,Х_n(t) функциональный определитель, гденазывается определителем Вронского.Свойства: 1)Если Х₁(t), Х₂(t),…,Х_n(t) являются линейно зависимыми на, тоW(t)≡0 для. Д-во. По определению линейной независимости. Это векторное тождество эквивалентно скалярным тождествам. Относительно постоянных а_iсистема (2) явл-ся линейной однородной алгебраической системой ур-ний, определитель которой совпадает с определителем Вронского (W(t)). Система (2) имеет нетривиальное решение приt. Лин. однор. Система урав-ний имеет нетривиальное решениеопределитель = 0W(t)≡0. 2) Если Х₁(t), Х₂(t),…,Х_n(t) явл-ся линейно независимыми начастными решениями одной и той же линейной однородной системыс непрерывными коэффициентами наа_ij(t), тоW(t)≠0. Д-во. (от противного):W(t₀)=0. Составим вспомогательную систему уравнений. Система (4) явл-ся линейной однородной алгебраической системой ур-ний;W(t₀)=0. Система (4) имеет ненулевое решение(по теореме) возьмемиз этих ненулевых решений.. По свойству 3) частных решений линейной однородной системы Х(t) явл-ся решением системы (3). В силу (4) наше решениеX(t₀)=0. С другой стороны, очевидно, что (3) имеет тривиальное решение;. При сформулированных условиях (3) удовлетворяет условиям теоремы существования и единственности решенияодно решение, удовлетворяющее начальному условию нулевому, т.е.противоречит независимости. В свойстве 2) дополнительное условие нашей функции явл-ся частным решением одной и той же лин. однор. системы (3) с непрерывными коэффициентами, Избавиться от дополнительного условия нельзя.

31) Неоднородные системы линейных дифференциальных уравнений. Общее решение. Принцип суперпозиции. Опр. 1 Система дифференциальных уравнений называется линейной, если она линейна относительно искомых функций х_i(t) и их производных. Линейная системаn-го порядка, имеет вид, где а_ij(t) (i,j=1,2,…,n) в количествеn²штук наз-ся коэффициентами системы (1),f_i(t) (nштук) наз-ся правыми частями системы (1). Пусть,,,. 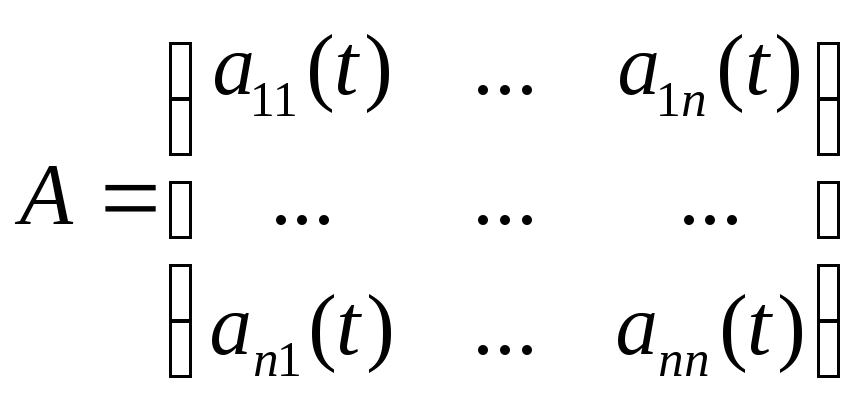Тогда в краткой векторной форме система (1) может быть записана в следующем виде. Соответствующая линейная однородная системаn-го порядка имеет видили. Свойства линейной неоднородной системы: 1)Еслиявл-ся решением лин. неоднородной системы, Х₀(t) явл-ся решением лин. однородной системы, тоявл-ся решением лин. неоднородной системы. Д-во.. 2)Принцип суперпозиции. Решением системы линейных уравнений, является сумма, решенийсистем уравнений. Д-во..Теорема(об общем решении линейной неоднородной системы уравнении). Общее решение линейной неоднородной системы (1)n-го порядка с непрерывными на отрезке [а,b] коэффициентами а_{i j} (t) (i,j=1,2,…,n) и правыми частямиf_i(t) равно сумме общего решениясоответствующей однородной системы и какого-либо частного решениярассматриваемой неоднородной системы. Д-во.- общее решение системы (1). Надо доказать: (3) – решение (1). То, что (3) явл-ся решением (1) следует из первого свойства частных решений. Нам нужно доказать более сильное утверждение: (3) – общее решение (1), т.е. оно содержит в себе все частные решения (1) без исключения. Т.к. в сформулированных условиях система 1) удовлетворяет условиям теоремы сущест. и единств. реш-я, то нам достаточно показать, что постоянные с_i в решении (3) всегда можно подобрать таким образом, чтобы (3)удовлетворяло Х(t₀) = Х₀(4), где. Для того, чтобы убедиться, подставим в (3) начальные условия (4):. Система ур-ний (5) относительно с_iявл-ся линейной неоднородной системой ур-ний, определитель которой = определителю Вронского -W(t₀). По второму свойству определителя ВронскогоW(t₀)≠0, т.к. функции линейно независ. частные решения (2)по теореме Кронекера-Копелли система (5) имеет имеет решение приправых частях и при.

32) Неоднородные системы линейных дифференциальных уравнений. Метод вариации постоянных. Опр. 1 Система дифференциальных уравнений называется линейной, если она линейна относительно искомых функций х_i(t) и их производных. Линейная системаn-го порядка, имеет вид, где а_ij(t) (i,j=1,2,…,n) в количествеn²штук наз-ся коэффициентами системы (1),f_i(t) (nштук) наз-ся правыми частями системы (1). Пусть,,,. Тогда в краткой векторной форме система (1) может быть записана в следующем виде. Соответствующая линейная однородная системаn-го порядка имеет видили.Построение общего решения линейной неоднородной системы уравнений осуществляется в 2 этапа: 1)находится общее решение соответствующей линейной однородной системы(2); 2)подбирается какое-нибудь одно решение системы (1). Метод подбирания частного решения: предположим, что обще решение найдено, а подобрать частное е можем. Тогда общее решение (1) может быть полученометодом вариации постоянных: пусть известны- общее решение (2);X(t) – общее решение (1) будем искать в форме. Для того, чтобы найти С_i(t), подставляем (3) в (1):,F_i– частное решение (2);. Относительно(4) – линейная неоднородная алгебраическая система, определитель которой =≠0 – ФСР соответствующей (2)(4) по теореме Кронекера-Копелли имеет единственное решение приправых частях(второй индекс указывает на номер решения, первый – номер неизвестной функции)подставляем в (3) и находим искомое решение. Метод вариации постоянных является универсальным.

33) Неоднородные системы линейных дифференциальных уравнений с постоянными коэффициентами. Метод неопределенных коэффициентов.Опр. 1Система дифференциальных уравнений называется линейной, если она линейна относительно искомых функций х_i(t) и их производных. Линейная системаn-го порядка, имеет вид, где а_ij(t) (i,j=1,2,…,n) в количествеn²штук наз-ся коэффициентами системы (1),f_i(t) (nштук) наз-ся правыми частями системы (1). Пусть,,,. Тогда в краткой векторной форме система (1) может быть записана в следующем виде. Соответствующая линейная однородная системаn-го порядка имеет видили. Частное решение системы (1) может быть найдено методом неопределенных коэффициентов:1)позволяет находить частные решения (1); 2)не является универсальным. Условия принимаемости:1)все коэффициенты –const; 2)все правые части – правые части специального вида, к ним относятся произведения показательных функций на многочлен, произведения показательных функций на сумму, произведенияsin,cosна многочлен, суммы функций этих двух видов. Применим алгоритм сведения системы уравнений к одному уравнению высокого порядка уравнений для линейной неоднородной системы с постоянными коэффициентами и специальными правыми частями:1)произведем почленное дифференцирование обеих частей; 2)из правой части полученного уравнения исключаем правые от искомой функции; 3)Эта система уравнений решалась относительно исключенной функции. Эта система уравнений линейна.; 4)

После применения этого алгоритма получим уравнение с одной искомой функцией (линейное с коэффициентами – константами и с правой частью специального вида). Метод неопределенных коэффициентов для (1):1) , где многочлен- степениm_i, где р – постоянная, называемая контрольным числом правых частей (единое для всех), тогда частное решение (1) нужно искать в форме, где- мн-н степениm+rс неопределенными коэффициентами,. Числоr=0, если р не явл-ся корнем характеристического уравнения, если жеpявл-ся корнем характеристического уравнения, тоr= кратности этого корня. Чтобы найти коэффициенты многочленов, надо решение (4) подставить в исходную систему (1) и приравнять коэффициенты при подобных членах в левых и правых частях уравнений, в результате чего получим систему линейных алгебраических уравнений относительно искомых коэффициентов.2) Если каждая из правых частей неоднородной системы (1) представима в виде,

где- многочлены, то неоднородная система имеет частное решение вида, где- многочлены с неопределенными коэффициентами степениm+r,m= наибольшей из степеней многочленов. Числоr=0, если контрольное число р+iqне явл-ся корнем характеристического уравнения; если р+iqявляется корнем характеристического уравнения, то г = кратности этого корня. Чтобы найти коэффициенты многочленов, надо решение (6) подставить в исходную систему и приравнять коэффициенты при подобных членах в левых и правых частях уравненийполучим систему линейных алгебраических уравнений относительно искомых коэффициентов.

Если из правы части (1) равны суммам нескольких функций вида (3) и (5) или разнотипным функциям вида (3) и (5), то частное решение (1) находится при помощи принципа суперпозиции: частное решение (1) с правыми частямиравно сумме частных решений соответствующих систем с правыми частями, равными каждому из наборов функций.

36) Понятие устойчивости. Простейшие типы точек покоя (случай кратных корней характеристического уравнения, вырожденные случаи). 1) . Рассмотрим 1а)2 линейно независимых собственных вектора матрицы А р =n-rang(A-kE)=2;rang(A-kE)=0A=kEсистема (1) примет вид- распавшаяся система уравнений.y=Cx, т.е. фазовый портрет имеет лучи.1а^-) k<0. Точка покоя явл-ся устойчивойточка покоя асимптотически устойчивая. Такой фазовый портрет наз-ся устойчивым дикритическим узлом. 1а⁺) k>0. Точка покоя покинет ε-окрестностьточка покоя неустойчива. Фазовый портрет наз-ся неустойчивым дикритическим узлом.1б) B₁– собственный вектор,B₂– присоединенный вектор, порожденный собственным. Общее решение, где. Применим к исходной фазовой плоскости Р аффинное преобразование, которое переводит Р в вспомогательную плоскость, в которойB₁иB₂ переходят в 2 взаимоортогональных единичных вектора.1б^-) k<0. Если у С₁и С₂, то мы получим новую фазовую траекторию системы (1), расположенную симметрично относительно начала координат по отношению к исходной траектории, заданной (3). Т.о. картина фазовых траекторий обладает симметрией относительно начала координатдостаточно построить фазовые траектории плоскоститолько в верхней полуплоскости. С₂>0 (т.к. в верхней полуплоскости);убывает к 0. При достаточно больших по модулю, неотрицательныхtС₁+С₂t>0. Точка покоя явл-ся устойчивой. Т.к.точка покоя явл-ся асимптотически устойчивой. Такой портрет наз-ся устойчивым вырожденным узлом.1б⁺) k>0. Точка покоя неустойчива. Фазовый портрет наз-ся неустойчивым вырожденным узлом. Сделаем аффинное преобразование изв.2)k=0. В этом случае нарушается условие единственности точки покоя.2а) . Если С₁=0, то все точки оси η неподвижны, они явл-ся точками покоя. Если С₁≠0, то:2а^-) ξ убывает и движение направлено к центру. Все точки покоя устойчивы, но неасимптотически. 2а⁺)ξ возрастает и движение направлено от центра.Все точки покоя будут неустойчивы. 2б)Существует 2 линейно независимых собственных вектора(частный случай 1а)). Вся плоскость Р состоит из точек покоя, они все устойчивые, но неасимптотически.2в). Существует 1 собственный векторB₁(частный случай 1б)). Если С₁=0, то все точки прямой ξ – точки покоя.. С₂≠0, то они неустойчивы.

41)Линейные и квазилинейные уравнения в частных производных первого порядка. Опр. 1 Квазилинейным уравнением первого порядка в частных производных наз-ся ур-ние вида, где- функции, определенные в некоторой области переменных (X,z).Опр. 2Уравнение (1) является линейным относительно производных от функцииzи линейным относительно самой функцииz, т.к. коэффициенты уравнения от искомой функции зависят и правая часть тоже. Если в уравнении (1) правая часть ≡ 0 , а все коэффициенты левой части не зависят от функцииz, то уравнение (1) – линейное однородное.. Рассмотрим квазилинейное уравнение с двумя независимыми переменными. Функцияzзависит от двух переменныхz=z(x,y), тогда квазилинейное уравнение примет вид. Рассмотрим векторную функцию. ФункцииP,Q,Rнепрерывны в той области, в которой мы будем их рассматривать.Опр.3Пространственная линия, касательная к которой ее точке параллельна векторув этой же точке наз-ся векторной линией этого поляFОпр.4 Поверхность, составленная из векторных линий поля Fназ-ся векторной поверхностью поляF.- вектор бесконечно малой касательной,. Система (4) явл-ся системой обыкновенных диф. ур-ний, записанная в симметричной формевекторную поверхность можно рассматривать как состоящую из семейства векторных линий, непрерывно зависящих от одного параметра, т.е. одно параметрическое семейство векторных линийповерхность в пространстве можно определить, задав вектор нормали к этой поверхности как функцию координат точек этой самой поверхности.z=f(x,y);;. Т.о. задача нахождения векторных поверхностей поляFэквивалентна задаче нахождения решения квазилинейного уравнения (3). Предположим, что искомая векторная поверхность задается неявным уравнениемu(x,y,z)=0и квазилинейное уравнение примет вид. Задача нахождения общих решений уравнения (3) и (6) эквивалентны. (6) – линейное однородное уравнение. В уравнении (3) количество независимых уравнений = 2, а в (6) их 3.. В дальнейшем будем рассматривать уравнение (3) и все будет справедливо для(6). Ур-ние (3) определяет все векторные поверхности поляF, ноиз этих векторных поверхностей состоит из векторных линий того жнее самого поля. Эти векторные линии определяются системой уравнений (4)обыкновенных диф. ур-ний, записанных в симметричной форме. Пусть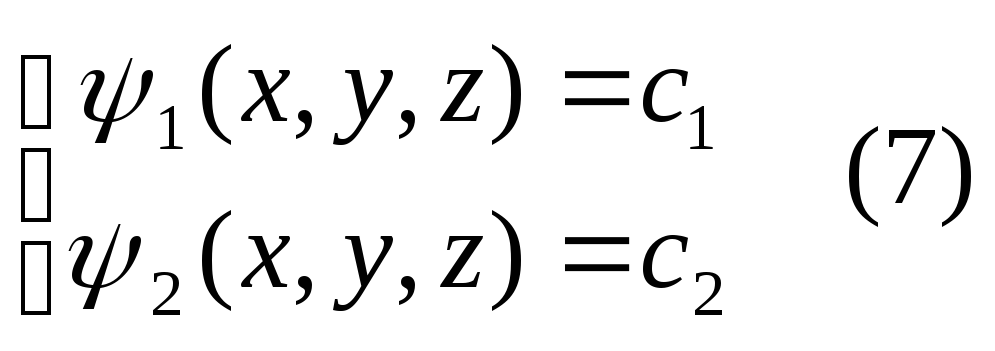- 2 независ. первых интеграла системы (4).Опр. 5 Ур-ние (7) в пространстве переменныхx,y,zопределяют линии, которые наз-ся интегр. линиями системы ур-ний (4) или характеристиками уравнения (3) (или(6)). Эти лини заполняют пространство целиком. Т.к. наши линии зависят от двух переменных, то они образуют двухпараметр. семейство. Для того, чтобы из двухпараметр. семейства (7) получить однопараметр. сем-во(поверхность), нужно избавиться от лишнего параметра. Пусть Ф(с₁, с₂)=0 – произвольная диф. функция. Подставляя (7) в последнее ур-ние, получим. Ур-ние (8) будет определять общее реш-ие (3) в неявной форме. Встречается и другая задача: найти векторную поверхность поляF, проходящую через заданную линию в пространстве. Пусть заданная линия имеет вид. Для того, чтобы получить конкретную функцию Ф, нужно объединить (7) и (9). Система из четырех уравнений. Из нее исключаемx,y,zФ(с₁, с₂)=0, где Ф – конкретная. Воспользовавшись этой функцией и (8), получим вектор. повер-ть, проходящую ч/з линию, определяемую (9). Эта поверхность наз-ся интегральной поверхностью (3)или (6).Т.о. чтобы найти общее реш-ие (3) или(6), нужно:1)Составить вспомогательную систему обыкновенных диф. ур-ний.; 2)найти 2 независимых первых интеграла этой системы; 3)Выписываем общее решение в виде (8). Если нужно найти ту интегр. поверх-ть (3)или(6), которая проходит ч/з заданную линию (9), то из четырех ур-ний 7) и 9) исключаемx,y.zи получаем конкретное уравнение, связывающее 2 параметра с₁, с₂ Ф(с₁, с₂)=0; 4)Подставляя в это ур-ние вместо с₁, с₂, левые части (7)получим ур-ние искомой поверх-ти. Если во второй задаче линия, определяемая (9), явл-ся характеристической ур-ния (3) или(6)наша задача неопределеннабесконечно много решений.