Понятие устойчивости. Теорема Ляпунова об асимптотической устойчивости.

Т2: (Ляпунова об асимптотической устойчивости)

Если существует диф. функция ,которая называется функцией Ляпунова в некоторой окрестности нач. координат удовлетворяет:

1)

2) 3)в некоторой сколь угодно малой окрестности.

-положит. const.,то явл. асимптотически устойчивым.

, то любая траектория (1) нач. точка которой находится в окрестности начала координат прине покинет предела E окрестности начала координат. То -функция Ляпунова вдоль любой нашей траектории будет функцией параметраt монотонно убывающей.

Известно, что любая монотонно убывающая функция ограниченная сверху имеет редел альфа.

т.к. ф. Ляпунова монотонно убывает.

Пусть , то траектория будет находиться вне достаточно малой окрестности начала координат. То траектория будет находиться вне малой окрестности начала координат. Но согласно этой окрестности начала координат/*dt

Интегрируем

При достаточно больших t правая часть будет отрицательной.То левая будет отриц..Это противоречит усл. (1).То.

Т.К. Ф. Ляпунова диф., то она непрерывна, то она достигает предельного значения в предельной точке. Точка в которой ф.Ляпунова=0-это начало координат.

-тривиальное решение, явл. асимптотически устойчивым.

ч.т.д.

№38

Понятие устойчивости. Теорема Четаева о неустойчивости.

Т3:( Теорема Четаева о неустойчивости.) Если существует диф. функция ,которая называется функцией Ляпунова в некоторой замкнутой окрестностиh-нач. координат удовлетворяет:

1) В сколь угодно малой окрестности нач. координат существует областьв которой ф. ЛяпуноваV>0 на границе этой области v=0.

Рисунок.

2) Внутри области производная вдоль траектории (1)

3)В области

-const.,то сис. (1) явл. неустойчивым.

Док-во

Возьмем произвольную точку внутри сколь угодно малой окрестности нач. координат внутрив качестве начальной точки нек. траектории сис (1)

Т.к. выполнимо 2, то вдоль нашей траектории пока она не покинет пределы h окрестности производная будет неотриц. т.е. пока траектория не покинет h окрестность, ф. Ляпунова будет монотонно возрастать фун-ей параметра t. То функция

То траектория будет находиться в области .

Пусть наша траектория при не покинетh окрестности.

Всюду выполняется:

интегрируем

Правая часть неограниченно

возрастающая функция, то левая тоже.То любая непрерывная функция на любом ограниченном мн-ве ограничена.

То по опр. точка покоя неустойчива. ч. т. д.

№40

Исследование на устойчивость по первому приближению.

1)Будем предполагать, что частное решение сис-мы (1) .

2)Будем считать, что прав.часть (1) диф. в некоторой окрестности нач. координат. Если это не так, то правую часть сис-мы (1) можно разложить по Тейлору и представить в виде: где-линейнейное слагаемое,-ост.член. в окрестности начала координат явл. бесконечно малыми фун-ями порядка выше 1 относительно-функции. Является ли тривиальное решение сис-мы (1) устойчивым или нет? Чаще всего применяют след. способ:1)пользуясь тем что малы их выбрасываем и заменяем (1): (2)-лин. однор. сис-ма с переем. коэффициенами. Решения (2) .Задачу исследования на устойчивость сис.(1) заменяют на задачу исследования тривиального решения (2)- это исследование на устойчивость по первому приближению.Опр1: система (2) наз. системой уравнений первого приближения по отношению к системе (1). Опр2: если все коэфф-ы из (1) и (2) постоянны, то система (1) наз-ся стационарной в первом приближении.Опр3: замена задачи исследования на устойчивость тривиального решений системы (1) на задачу системы (2) наз. исследованием на устойчивость по первому приближению. В первые такое обоснование этого приема дал Ляпунов.

Т1:Если сис-ма уравнений (1) стационарна в первом приближении, а остаточные член функции удовлетворяют:,гдеи все корни характеристического уравнения:

имеют отриц. действительные части, то трив. решения ,как сис-мы (1), так сис-мы (2) являются асимптотически устойчивыми и возможно исследование на устойчивость по 1 приближению.Т2:Если система (1) стационарна в первом приближении, а остаточные члены функции удовлетворяют условиям предыдущей теоремы и кроме того хотя бы один из корней (3) имеет положительную действительную часть, то тривиальное решение как системы (1), так системы (2) не устойчиво, возможно исследование по первому приближению. Условия теорем охватывают не все случаи возможные для корней уравнения (3). Под условием теорем не попадает критический случай: все корни (3) имеют не положительную действительную часть и хотя бы один из корней имеет нулевую действительную часть. В этом случае на устойчивость системы (1) влияют остаточные члены ,то исследование на устойчивость по первому приближению невозможно. Но в общем случае доказательства теоремы явл-ся сложным и громоздким. Мы ограничимся док-ом первой теоремы в частном случае.

Докажем т-му при дополнительном условии: все корни ур (3) явл. действительными и различными.,R-вектор столбец ,Х-вектор столбец , А-матрица из.

Сделаем невырожденное линейное преобразование фун Х: Х=ВУ(4), У-постоянная матрица.

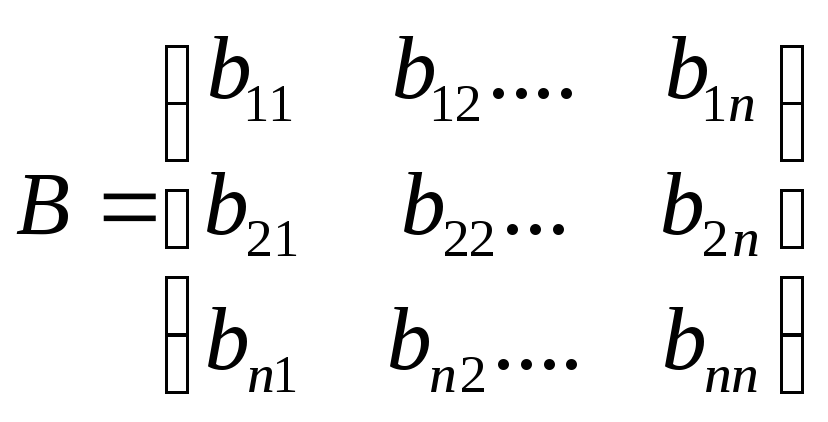
.подставим (4) в (2):

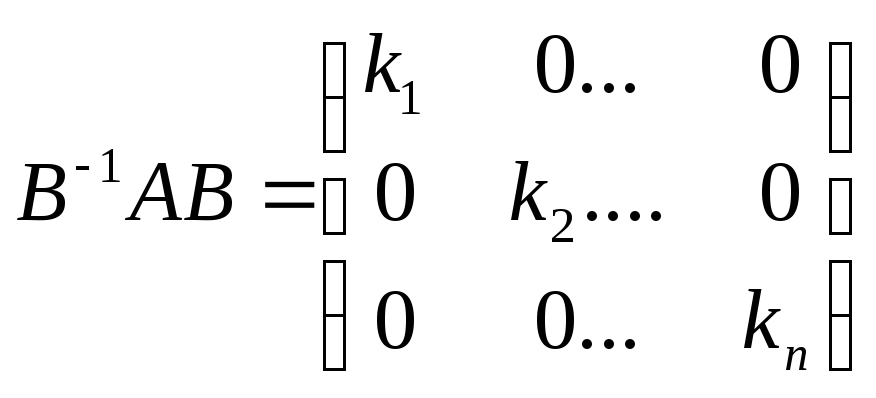Матрицу В можно подобрать так, чтобы она была диагональной. В сосоит из собственных векторов матрицы А.Сис-ма (2) преобретает след. вид: .Решение как у (5),так у (6) асимптотически устойчиво, то отсюда следовать асимптотическая устойчивость сис-мы (1) и (2).(5)-распавшаяся сис-ма. Решение(5):-монотонно убывает т.к.-тривиальное решение сис-мы (5) асимптотически устойчиво. Чтобы доказать асимптотическую устойчивость(6) воспользуемся т.Ляпунова об асимптотической устойчивости.Проверим условия теоремы:

1)

2) при достаточно малой окрестности начала координат.

3)

ис-ма с перем. и заменяем (1):

00000000000000000000000000000000000

№42