1) Уравнения с разделяющимися переменными. Уравнением с разделяющимися переменными называется дифференциальное уравнение, которое может быть представлено в виде: y^/=f(x)g(y) или в виде f(x)g(y)dx+h(x)p(y)dy=0. Для нахождения общего решения этого уравнения с разделяющимися переменными нужно разделить переменные, т. е. путем деления обеих частей уравнения на произведение g(y)h(x) добиться того, чтобы в преобразованном уравнении коэффициент при dx являлся бы функцией только от переменной x, а коэффициент при dy – функцией только от переменной y: . Уравнение этого вида называется дифференциальным уравнением с разделенными переменными. Интегрируя, найдем общий интеграл. Необходимо отметить, что деление наg(y)h(x) может привести к потере частных решений, обращающихся в нуль произведение g(y)h(x). Уравнение, правая часть которого является функцией линейного аргумента: y^/=f(ax+by+c), где a и b – постоянные, сводится к уравнению с разделяющимися переменными с помощью замены исходной переменной z=ax+by+c. Вычисляя производную от новой искомой функции z^/=a+by^/ и используя исходное уравнение, получаем: z^/=a+bf(z), откуда . Интегрируя, получим общий интеграл:, в котором осталось сделать обратную замену переменнойz=ax+by+c.

2) Однородные дифференциальные уравнения. Однородным называется уравнение, которое может быть представлено в виде: y^/=f(y/x) или: M(x,y)dx+N(x,y)dy=0, где M(x,y) и N(x,y) – однородные функции одинаковой степени однородности. Функция F(x,y) называется однородной степени n, если для любого t>0 выполняется тождество: F(tx,ty)≡tⁿF(x,y). Однородное уравнение сводится к уравнению с разделяющимися переменными с помощью замены искомой переменной z=y/x или y=xz. Дифференцируя указанную замену по x, получаем y^/=xz^/+z для первой формы однородного уравнения и dy=xdz+zdx для второй. Подставляя найденную производную в исходное уравнение, получаем уравнение с разделяющимися переменными: xz^/+z=f(z), или . Интегрируя, получаем общий интеграл:, в котором осталось сделать обратную замену переменнойz=y/x. Уравнение с правой частью в виде функции дробно-линейного аргумента , гдеa₁, b₁, c₁, a₂, b_2, c₂ – постоянные, преобразуется в однородное уравнение с помощью введения новых переменных u и v по формулам x=u+x₀, y=v+y₀ (1), где x₀ и y₀ – решение системы линейных алгебраических уравнений a₁x+b₁y+c₁=0, a₂x+b₂y+c₂=0. Так как , то, подставляя (1) в исходное уравнение, получаем, то есть получаем однородное уравнение вида. Описанный метод неприменим в случае параллельности прямых (2). Но в этом случае коэффициенты в уравнениях (2) пропорциональныa₂/a₁=b₂/b₁=k, и исходное уравнение можно записать в виде , и заменой переменнойz=a₁x+b₁y свести к уравнению с разделяющимися переменными.

3) Линейные дифференциальные уравнения первого порядка. Метод вариации постоянной. Линейным дифференциальным уравнением первого порядка называется уравне- ние линейное относительно неизвестной функции и ее производной. Линейное уравнение имеет вид: y^/+p(x)y=f(x) (1). Если f(x)≡0, то уравнение (1) называется линейным однородным. Для интегрирования неоднородного линейного уравнения применяется метод вариации постоянной, который состоит в следующем. Сначала интегрируется соответствующее однородное линейное уравнение y^/+p(x)dx, в котором переменные разделяются: , откуда, интегрируя, получаем, где С – произвольная постоянная. Решение исходного уравнения ищем в виде(2), где С(х) – новая неизвестная функция переменной х. Вычисляя производнуюdy/dx и подставляя ее и (2) в исходное уравнение (1), после приведения подобных получаем , откуда, интегрируя, находим функцию С(х) и после ее подстановки в (2) получаем общее решение исходного уравнения.

4) Уравнения Бернулли и Риккати. Уравнение Бернулли, имеющее вид y^/+p(x)y=f(x)yⁿ, n=1, заменой переменной z=y^1-n сводится к линейному уравнению. Однако, это уравнение можно проинтегрировать методом вариации постоянной. Сначала интегрируем соответствующее однородное уравнение y^/+p(x)y=0, в котором переменные разделяются: , откуда, интегрируя, получаем, где С – произвольная постоянная. Решение исходного неоднородного уравнения Бернулли ищем в виде(1), где С(х) – новая неизвестная функция переменной х. Вычисляя производнуюdy/dx и подставляя ее и (1) в исходное уравнение, после приведения подобных получаем - уравнение с разделяющимися переменными относительно неизвестной функции С(х), интегрируя которое, находим С(х) и после подстановки в (1) получаем общее решение исходного уравнения. Уравнение Риккати, имеющее видy^/+p(x)y+q(x)y²=f(x), в общем случае не интегрируется в квадратах. Однако, если известно одно частное решение u(x) этого уравнения, то оно заменой y=u+z, где z(x) – новая неизвестная функция, сводится к уравнению Бернулли. Действительно, подставляя указанную замену в исходное уравнение, получим u^/+z^/+p(x)(u+z)+q(x)(u+z)²=f(x) или, учитывая, что u^/+p(x)u+q(x)u²≡f(x), после приведения подобных будем иметь уравнение Бернулли: z^/+(p(x)+2q(x)u(x))z+q(x)z²=0.

5) Уравнения в полных дифференциалах. Интегрирующий множитель. Уравнение, записанное в симметричной форме M(x,y)dx+N(x,y)dy=0 (1), называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции u(x,y) двух независимых переменных, то есть . В этом случае общий интеграл исходного уравнения имеет вид:u(x,y)=C, где С – произвольная постоянная. Для того чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие Эйлера: . Для нахождения функцииu(x,y) воспользуемся равенствами ,(2). Интегрируя первое из равенств (2) по х (считаяy постоянной), имеем (3), где φ(y) – произвольная функция от y. Дифференцируя полученное выражение по y и подставляя во второе из равенств (2), получаем . Правая часть последнего уравнения в силу условия Эйлера не зависит от х. Поэтому, интегрируя его поy, находим , подставляя результат в (3), получим искомую функцию. В некоторых случаях, когда уравнение (1) не является уравнением в полных дифференциалах, удается подобрать функциюпосле умножения на которую левая часть уравнения (1) превращает в полный дифференциал. Такая функцияназывается интегрирующим множителем. Из определения интегрирующего множителя следует и условия Эйлера, следует что он должен удовлетворять уравнению, или

(6). В общем случае задача интегрирования этого уравнения в частных производных не легче, чем задача интегрирования уравнения (1), однако в некоторых частных случаях это уравнение упрощается и интегрирующий множитель μ легко находится. 1. Уравнение (1) имеет интегрирующий множитель, зависящий только от х. В этом случае уравнение (6) принимает вид 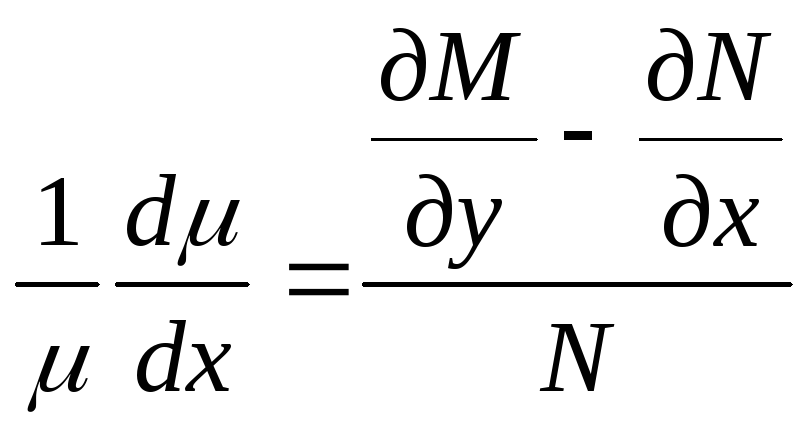. В этом уравнении левая часть является функцией только отx. Значит и правая часть должна быть функцией только от х, в противном случае интегрирующего множителя вида μ=μ(х) не существует. 2. Уравнение (1) имеет интегрирующий множитель, зависящий только от y. В этом случае уравнение (6) принимает вид . В этом уравнении левая часть является функцией только отy. Значит и правая часть должна быть функцией только от y, в противном случае интегрирующего множителя вида μ=μ(y) не существует. 3. Уравнение (1) имеет интегрирующий множитель μ=μ(z(x,y)), где z(x,y) – известная функция. В этом случае уравнение (6) принимает вид . 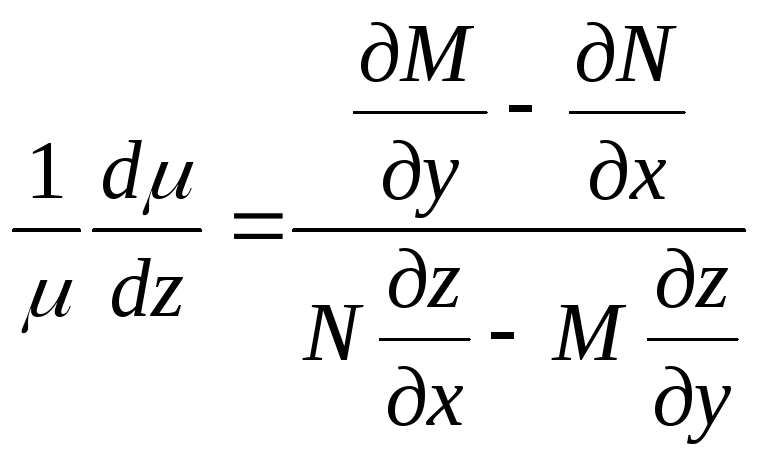В этом уравнении левая часть является функцией только отz. Значит и правая часть должна быть функцией только от z, в противном случае интегрирующего множителя вида μ=μ(z) не существует.

13. Общее решение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами (случай простых корней характеристического уравнения). Частные решения линейного однородного уравнения n-го порядка с постоянными коэффициентами a₀y⁽ⁿ⁾+a₁y^(n-1)+…+a_n-1y^/+a_ny=0 можно искать в виде y=e^kx, где k – некоторая постоянная. Так как y^/=ke^kx, y^//=k²e^kx, … , y⁽ⁿ⁾=kⁿe^kx, то подставляя в исходное дифференциальное уравнение имеем: (a₀kⁿ+a₁k^n-1+…+a_n-1k+a_n)e^kx=0. Сокращая на необращающийся в нуль множитель e^kx, получим алгебраическое уравнение n-ой степени, называемое характеристическим: a₀kⁿ+a₁k^n-1+…+a_n-1k+a_n=0. Это уравнение определяет те значения постоянной k, при которых функция y=e^kx является частным решением линейного однородного уравнения (1). В зависимости от рода корней характеристического уравнения (2) возможен случай: Если все корни k₁, k₂,…,k_n характеристического уравнения действительны и различны, то тем самым найдено n линейно независимых частных решений исходного уравнения, то есть найдена его фундаментальная система решений. Следовательно,, гдеC_i – произвольные постоянные, является общим решением исходного уравнения.

14. Общее решение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами (случай кратных корней характеристического уравнения). Частные решения линейного однородного уравнения n-го порядка с постоянными коэффициентами a₀y⁽ⁿ⁾+a₁y^(n-1)+…+a_n-1y^/+a_ny=0 можно искать в виде y=e^kx, где k – некоторая постоянная. Так как y^/=ke^kx, y^//=k²e^kx, … , y⁽ⁿ⁾=kⁿe^kx, то подставляя в исходное дифференциальное уравнение имеем: (a₀kⁿ+a₁k^n-1+…+a_n-1k+a_n)e^kx=0. Сокращая на необращающийся в нуль множитель e^kx, получим алгебраическое уравнение n-ой степени, называемое характеристическим: a₀kⁿ+a₁k^n-1+…+a_n-1k+a_n=0. Это уравнение определяет те значения постоянной k, при которых функция y=e^kx является частным решением линейного однородного уравнения (1). В зависимости от рода корней характеристического уравнения (2) возможен случай: Если среди корней характеристического уравнения имеются кратные, то число линейно независимых частных решений вида будет меньшеn. Пусть корень k имеет кратность r, тогда частными решениями исходного уравнения, соответствующими этому корню, будут r функций: e^kx, xe^kx,x²e^kx,…,x^r-1e^kx,e^kix (здесь не ki, а k_i)(i=1,…,n-r), которые образуют фундаментальную систему решений исходного уравнения. Следовательно, , гдеC_i – произвольные постоянные, является общим решением исходного уравнения. Если характеристическое уравнение имеет несколько кратных корней, то в последней формуле произойдут очевидные изменения.

6) Дифференциальные уравнения, не разрешенные относительно производной. Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид F(x, у, у')=0 (1). Пусть уравнение (1), не разрешенное относительно производной, легко разрешимо относительно производной. Чаще всего это возможно для уравнения первого порядка n-ой степени относительно у': , где р,q, r - заданные функции переменных х и у. Если найдены n вещественных корней этого уравнения, то оно распадается на n уравнений, разрешенных относительно производной: у'=f₁(х, у), y'=f₂(x, у), … y'=f_n(x,y),

каждое из которых решается отдельно (если это возможно) подходящим методом интегрирования уравнения, разрешенного относительно производной. Если левая часть уравнения (1) не содержит независимой переменной х или искомой функции у, или того и другого вместе, то оно называется неполным. Рассмотрим некоторые из частных случаев. 1. Простейшим из неполных уравнений является уравнение, со­держащее только производную: F(y')=0. Общий интеграл такого уравнения находится следующим образом. Предположим, что это уравнение имеет некоторое (конечное или бес­конечное) число вещественных корней y'=k_i, (i = l, 2, ...) (2), где k_i - некоторые постоянные, так что имеют место тождества: F(k_i)=0, (i=1,2,…) (3). Интегрируя уравнения (2), находим у = k_ix+С, откуда . После подстановки этого значения k_i в тождество (3) приходим к одному соотношению . Это соотношение и есть общий интеграл исходного уравнения. 2. Уравнение видаF(x, у')=0, не разрешенное относительно производной и не содержащее искомой функции, интегрируется методом введения параметра t и заменой исходного уравнения двумя уравнениями: x=φ(t), y^/=ψ(t). Так как dy = y'dx, то в данном случае , откудаи, следовательно, общее решение исходного уравнения в параметрической форме определяется следующими уравнениями:,. Если исходное уравнение легко разрешимо относительно х:

то удобно в качестве параметра ввести у'= t. Тогда ,,. 3. Уравнение видаF(y,y')=0, не разрешенное относительно производной и не содержащее независи­мой переменной, также интегрируется методом введения параметра t и заменой исходного уравнения двумя уравнениями: ,. Так какdy = y'dx, то в данном случае , откудаи, следовательно, общее решение исходного уравнения в параметриче­ской форме определяется следующими уравнениями:,. Если исходное уравнение легко разрешимо относительно у:, то удобно в качестве параметра ввестиy'=t. Тогда ,,. 4. Если уравнениеf(z, у, у')=0 разрешимо относительно искомой функции, то есть приводится к виду y=f{x,у'), то, считая х и р=у' параметрами, получаем следующее пapaметрическое представление исходного уравнения: y=f(x,p), y^/=p. Так как ,, то, учитывая, что у'=р, получаем уравнение, разрешенное относительно производной:. Интегрируя полученное уравнение (если оно интегрируется в квадратурах), получим Ф(х, р, С)=0. Совокупность уравнений Ф(х, р, С)=0,y=f(x,p) является общим решением исходного уравнения в параметрической фор­ме. 5. Если уравнение F(x, у, у')=0 разрешимо относительно независимой переменной: x=f(y,y^/), то, считая у и р=у' параметрами, получаем следующее параметр кое представление исходного уравнения: x=f(y,p), y'=р. Так как , то после подстановки в соотношениеdy=y^/dx и деления на dy имеем , и, учитывая, что у'=р, получаем уравнение, разрешимое относительно производной:. Интегрируя полученное уравнение (если оно интегрируется квадратурах), получим Ф{у, р, С)=0. Совокупность уравнений Ф(y,p,С)=0, x=f(y, р) является общим решением исходного уравнения в параметрической форме.

7) Уравнения Лагранжа и Клеро. Уравнением Лагранжа называется линейное относительно х,у уравнение . Для интегрирования этого уравнения вводим параметр р = у'. Тогда(1). Дифференцируя по переменной х и полагая у'=р, получим, или. Это линейное относительно х иуравнение легко интегрирует­ся, например, методом вариации постоянной. Найдя его общее решение х=χ(р,С) и присоединяя к нему соотношение (1), получаем общее решение ис­ходного уравнения в параметрической форме: х=χ(р,С),. В процессе решения при делении намогут быть потеряны решения р = р_i (i=l,2, ...), где p_i - корни уравнения p-φ(p)=0, которым соответствуют следующие решения исходного уравнения у = p_ix+ψ(p_i). Уравнением Клеро называется частный случай уравнения Лагранжа: у = ху'+ψ(у^/). Для интегрирования этого уравнения вводим параметр р = у'. Тогда y=xp+ψ(p) (2). Дифференцируя по переменной х и полагая у'=р, получим , или. Откудаили. В первом случае р=С и, исключая р из (2), получим:y=Cx+ψ(C) (3) - однопараметрическое семейство интегральных прямых. Во втором случае решение определяется двумя уравнениями x=-ψ^/(p), y=-pψ^/(p)+ψ(p) в параметрической форме. Можно показать, что интегральная кривая, определяемая последними уравнениями является огибающей семейства интегральных прямых (3).

11)Фундаментальная система решений линейного однородного дифференциального уравнения n-го порядка. Общее решение. Понижение порядка. Теорема. Общим решением при а≤х≤b линейного однородного уравнения (3) с непрерывными на отрезке а≤х≤b коэффициентами a_i(x),а₀(x)≠0 (i=1,2,...,n) является линейная комбинация n линейно независимых на том же отрезке частных решений у_i(х) (i = 1, 2,...,n) с произвольными постоянными коэффициентами C_i. Любые n линейно независимых частных решений линейного одно­родного уравнения n-гo порядка называются его фундаментальной сис­темой решений. Если известно нетривиальное частное решение у₁(х) линейного однородного уравнения (3), то его порядок можно понизить на едини­цу (сохраняя его линейность и однородность) подстановкой

, где u(x) - новая неизвестная функция. Если известно k линейно независимых частных решений уравнения (3), то его порядок можно понизить на k единиц. Теорема. Общее решение на отрезке а≤х≤b линейного неоднородного уравнения (1) с непрерывными на том же отрезке а≤х≤b коэффициентами a_i(x), a₀(x)≠0 (i = l, 2, ...,n) и правой частью f(x) равно сумме общего решения у₀(х) соответствующего однородного уравнения (3) и какого-нибудь частного решения неоднородного уравнения.

Если правая часть уравнения равна сумме нескольких функций f(х)=f₁(x)+f₂(x)+…+f_m(x), то частное решение неоднородного уравнения находится при помощи принципа суперпозиции. Частное решение линейного уравнения (1) правой частью (4) равно сумме частных решений уравнений с той же левой, частью и правыми частями, равными каждой из функций f₁(x),f₂(x),…,f_m(x). Если известна фундаментальная система y₁(x),у₂(x),...,у_n(x) решений однородного линейного уравнения (3), то общее решение неоднородного линейного уравнения (1) может быть найдено методом вариации постоянных, который заключается в следующем. Общее реш ние неоднородного уравнения (1) ищется в виде

у=С₁(х)у₁(х)+C₂(x)y₂(x)+...+Сn(х)у_n(х), где новые неизвестные функции C_i(x) (i = 1,...,n) определяются системы уравнений ,

… , , которая является системой линейных неоднородных алгебраических уравнений относительно (i=1,2,...,n). Определитель этой системы отличен от нуля, поэтому она всегда имеет единственное решение (i=l,2,...,n), откуда, интегрируя, находим , и после подстановки в (5) получаем общее решение уравнения (1).

8) Дифференциальные уравнения порядка выше первого. Простейшие случаи понижения порядка. Рассмотрим простейшие случаи, допускающие понижения порядка. 1. Дифференциальное уравнение F(x,y^(k),…,y⁽ⁿ⁾) =0, не содержащее искомой функции y и ее младших производных до порядка k-1 включительно, допускает понижение порядка на k единиц заменой переменной u=y^(k), где u(x) – новая искомая функция. Действительно, после замены переменных исходное уравнение принимает вид: F(x,u,u^/,…,u^(n-k))=0. Интегрируя это уравнение и определяя новую искомую функцию u=u(x,C₁,…,C_n-k), можно найти функцию y k-кратным интегрированием уравнения y^(k)=u(x,C₁,…,C_n-k). 2. Дифференциальное уравнение F(y,y^/,y^//,…,y⁽ⁿ⁾)=0, не содержащее независимой переменной, допускает понижение порядка на единицу путем замены обеих переменных. В качестве новой искомой функции выбирается p=y^/, а в качестве новой независимой переменной принимается y, то есть p=p(y). При этом все производные надо выразить через производные от новой искомой функцииp(y) по y. По правилу дифференцирования сложной функции получаем ,и аналогично для производных более высокого порядка. При этом очевидно, что производныевыражается через производные порядка не вышеk-1 от p по y, что и приводит к понижению порядка на единицу, то есть исходное уравнение после замены переменных принимает вид . 3. Если левая часть уравненияn-го порядка F(x,y,y^/,y^//,…,y⁽ⁿ⁾)=0 является некоторой производной некоторой функции Ф(x,y,y^/,y^//,…,y^(n-1)), то есть , то непосредственно интегрированием получаем уравнение Ф(x,y,y^/,y^//,…,y^(n-1))=C, которое является уравнением (n-1)-го порядка и называется первым интегралом исходного уравнения. Иногда левая часть исходного уравнения становится точной производной лишь после умножения на множитель μ(x,y,y^/,…,y^(n-1)), который называется интегрирующим множителем. 4. Однородное уравнение n-го порядка F(x,y,y^/,y^//,…,y⁽ⁿ⁾)=0, для которого при некотором k и любом t справедливо тождество F(x,ty,ty^/,ty^//,…,ty⁽ⁿ⁾)≡t^k F(x,y,y^/,y^//,…,y⁽ⁿ⁾), допускает понижение порядка на единицу с помощью подстановки , гдеz(x) – новая неизвестная функция. Действительно, дифференцируя, получаем ,,, … ,. Убедиться в справедливости последнего равенства можно методом индукции. Подставляя полученные равенства в исходное уравнение и замечая, что в силу однородности множитель, можно вынести за знак функцииF, получим или, сокращая на, получаем уравнение (n-1)-го порядка . 5. Обобщенное однородное уравнениеn-го порядка F(x,y,y^/,y^//,…,y⁽ⁿ⁾)=0, для которого при некоторых k, p и любом t справедливо тождество , допускает понижение порядка на единицу заменой обеих переменныхx=e^t, y=z(t)e^kt (1), где t – новая независимая переменная; z(t) – новая искомая функция. Выразим производные от функции y по переменной x через производные от функции z по переменной t. По правилу дифференцирования сложной функции ,,, … ,, гдеg – некоторая функция n+1 переменной. Подставляя (1) и полученные выражения производных в исходное уравнение, получим уравнение следующего вида: . В силу обобщенной однородности исходного уравнения множительe^pt можно вынести за знак функции F. В результате после сокращения получим уравнение n-го порядка. . Это уравнение не содержит независимой переменнойt и поэтому допускает понижение порядка на единицу.

9) Линейное однородное дифференциальное уравнение n-го порядка. Линейным дифференциальным уравнением n-го порядка называется уравнение, линейное относительно неизвестной функции и ее произ­водных и, следовательно, имеющее вид

(1). Если правая часть f(х)≡0, то уравнение называется линейным однородным, так как оно однородно относительно неизвестной функции у и ее производных. Функции у₁(х), у₂(x), ..., у_n(х) называются линейно зависимы­ми на некотором отрезке изменения х, а≤х≤b, если существуют постоянные a₁,a₂,..., a_n такие, что на том же отрезке a₁y₁(x)+a₂y₂(x)+…+a_ny_n(x)≡0 (2), причем хотя бы одно из a_i≠0. Если же тождество (2) справедливо лишь при а₁=а₂₌...=a_n=0, то функции у₁(х),у₂(х),...,у_n(х) называются линейно независимыми на отрезке а≤х≤b.

Теорема. Общим решением при а≤х≤b линейного однородного уравнения (3) с непрерывными на отрезке а≤х≤b коэффициентами a_i(x),а₀(x)≠0 (i=1,2,...,n) является линейная комбинация n линейно независимых на том же отрезке частных решений у_i(х) (i = 1, 2,...,n) с произвольными постоянными коэффициентами C_i. Любые n линейно независимых частных решений линейного одно­родного уравнения n-гo порядка называются его фундаментальной сис­темой решений. Если известно нетривиальное частное решение у₁(х) линейного однородного уравнения (3), то его порядок можно понизить на едини­цу (сохраняя его линейность и однородность) подстановкой

, где u(x) - новая неизвестная функция. Если известно k линейно независимых частных решений уравнения (3), то его порядок можно понизить на k единиц. Теорема. Общее решение на отрезке а≤х≤b линейного неоднородного уравнения (1) с непрерывными на том же отрезке а≤х≤b коэффициентами a_i(x), a₀(x)≠0 (i = l, 2, ...,n) и правой частью f(x) равно сумме общего решения у₀(х) соответствующего однородного уравнения (3) и какого-нибудь частного решения неоднородного уравнения.

Если правая часть уравнения равна сумме нескольких функций f(х)=f₁(x)+f₂(x)+…+f_m(x), то частное решение неоднородного уравнения находится при помощи принципа суперпозиции. Частное решение линейного уравнения (1) правой частью (4) равно сумме частных решений уравнений с той же левой, частью и правыми частями, равными каждой из функций f₁(x),f₂(x),…,f_m(x). Если известна фундаментальная система y₁(x),у₂(x),...,у_n(x) решений однородного линейного уравнения (3), то общее решение неоднородного линейного уравнения (1) может быть найдено методом вариации постоянных, который заключается в следующем. Общее реш ние неоднородного уравнения (1) ищется в виде

у=С₁(х)у₁(х)+C₂(x)y₂(x)+...+Сn(х)у_n(х), где новые неизвестные функции C_i(x) (i = 1,...,n) определяются системы уравнений ……………………

, которая является системой линейных неоднородных алгебраических уравнений относительно (i=1,2,...,n). Определитель этой системы отличен от нуля, поэтому она всегда имеет единственное решение (i=l,2,...,n), откуда, интегрируя, находим , и после подстановки в (5) получаем общее решение уравнения (1).

10) Определитель Вронского. Определение. Если есть x₁(t),x₂(t),…,x_n(t), тот функцион. определитель состоит из компонентов этих функций. 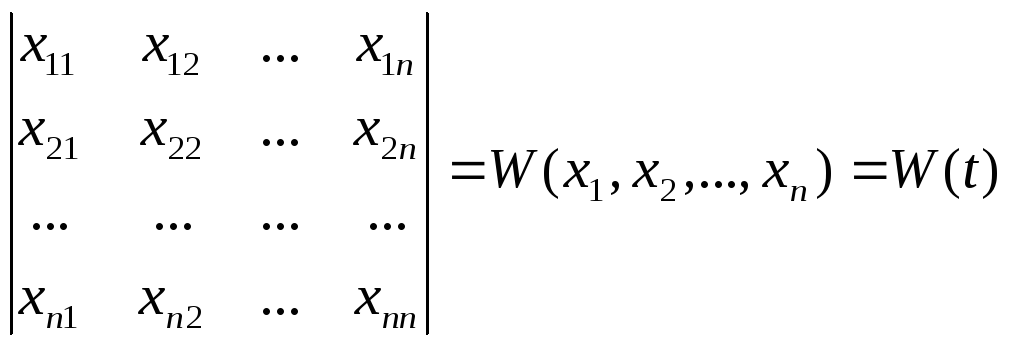называется определителем Вронского нашихn-функций. Свойства: 1. Если x₁(t), x₂(t),…,x_n(t) является линейно зависимым на (a,b), то на (a,b). 2. Если x₁(t), x₂(t),…,x_n(t) является линейно независимой на (a,b) частными решениями линейной однородной системы с непрерывными на том же отрезке (a,b) коэффициенты a_ij(t), то определитель Вронского этих функций не может обратиться в нуль ни в одной точке нашего отрезка.

, (i=1...n) (здесь всюду второй индекс указывает номер решения а первый номер неизвестной ф-ции), определитель этой ф-ции всегда отличен от нуля, поэтому она всегда имеет единственное решение , (i=1...n), откуда находим . В отличие от метода неопрю коэфф., метод вариации постоянных может применяться для систем ур-й и с постоянными и с переменными коэфф-ми.

15. Общее решение линейного неоднородного дифура n-го порядка. Принцип суперпозиции.

Такое ур-е имеет вид (1) его общее решение равно сумме сумме общего решения, соотв-го однородного урав-я.и какого либо частного решениянеоднородного уравнения. Если правая часть ур-я (1) имеет специальный вид(2), где р- постоянная называемая контрольным числом правой части-многочлен степениm, то неоднородное ур-е имеет частное решение вида (3), где-многочлен степениm с неопред.-ми коэфф-ми, число r=0, если р не является корнем характеристич.-го ур-я. Если р яв-ся корнем хар-го ур-я- такой случай наз-ся резонансным, то r равно кратности этого корня. Что бы найти коэфф-ты многочлена надо решение подставить в исх-е уравнение и приравнять коэфф-ты при подобных членах в левой и правой частях ур-я. В итоге получим систему линейных алгебраических ур-ий. Если правая часть ур-я (1) имеет специальный вид(4), гдеP(x) и Q(x)- многочлены то неоднородное ур-е имеет частное решение вида: (5) гдеимногочлены с неопр-ми коэфф-ми степениm равной наибольшей из степеней многочленов P(x) и Q(x), число r=0, если контрольное число p+iq не явл-ся корнем хар-го ур-я, если является то это резонасный случай и r равно кратности этого корня. Что бы найти коэфф-ты многочленов инадо решение (5) подставить в исходное уравнение и приравнять коэфф-ты при подобных членах в левой и правой частях уравнения. В итоге получим систему линейных алгебраич-х ур-й отн-но искомых коэфф-тов. Если правая часть ур-я равна сумме нескольких функций вида (2) и (4), то частное решение неоднород-го ур-я находится при помощипринципа суперпозиции.

Частное решение линейного ур-я (1) с правой частью равно сумме частных решений уравнений с той же левой частью и правыми частями равными каждой из ф-ций,, ... ,.

16. Линейное неоднородное дифф.Ур. N-го порядка. Метод вариации постоянных.

Такое ур-е имеет вид (1) Если известна фундаментальная система, решений однородного линейного уравнения, то общее решение неоднородного линейного ур-я м.б. найденометодом вариации постоянных: общее решение неоднородного ур-я (1) ищется в виде , где функции, определяются из с.у.,,...,, которая явл-ся системой неоднородных алгебраич-х ур-й отн-но, откуда находим:

17. Линейное неоднородное дифф.Ур. N-го порядка с пост-ми. Коэфф-ми. Метод неопр. Коэфф.

Имеет такой вид: (1). во многих случаях удается подобрать частн. решен. ур-я (1), а значит появл-ся возм. воспольз-ся теор. об общем решении неоднородного лин. ур-я. Т.к. находит решения соотв. однородного ур-я мы умеем. Для нахождения частного решения ур-я (1) можно исп. метод неопр. коэфф.

, , чтобы убедиться что ур-е (1) действительно явл-ся решением многочленам подставимв уравнение (1):,, ... ,;. Если правая часть ур-я (1) имеет многочленаs-той степени и последний коэфф. левой части не равен 0, то его решением явл-ся многочлен той же самой степени.