Дифуры ответы экзамен лето 2012

1) Уравнения с разделяющимися переменными и приводящиеся к ним.. Опр. 1 Уравнением с разделяющимися переменными называется дифференциальное уравнение, которое может быть представлено в виде: y^/=f(x)g(y) или в виде f(x)g(y)dx+h(x)p(y)dy=0 (0). Для нахождения общего решения этого уравнения с разделяющимися переменными нужно разделить переменные, т. е. путем деления обеих частей уравнения на произведение g(y)h(x) добиться того, чтобы в преобразованном уравнении коэффициент при dx являлся бы функцией только от переменной x, а коэффициент при dy – функцией только от переменной y: . Опр. 2 Уравнение этого вида называется дифференциальным уравнением с разделенными переменными. Интегрируя, найдем общий интеграл . В общем случае (0) и (1) неэквивалентны, т.е. у них не одинаковы множества решений. Связано это с тем, что деление на g(y)h(x) может привести к потере некоторых частных решений (0), обращающихся в нуль произведение g(y)h(x). Поэтому в конкретном случае необходимо:1)необходимо находить все решения уравнения g(y)h(x)=0. Эти функции будем называть подозрительными; 2)из подозрительных функций необходимо по отдельности проверить, не явл-ся ли она решением (0). Та из них, которая явл-ся решением (0) наз-ся потерянным решением, т.к. эта функция явл-ся решением (0), но не явл-ся решением (1). После того как оба интеграла в (2) вычислены, получим конечное уравнение, связывающее х и у, в котором нет ни производных, ни дифференциалов. . Из этого уравнения можно выразить переменную, либо х , либо у ч/з другую, т.е. получить решение уравнения в явной форме, но это удается не всегда. В случае, если уравнение (2) невозможно решить относительно у или х , мы все равно считаем уравнение (1) решенным, но решение получено в неявной форме. Опр 3. Конечное уравнение вида наз-ся частным интегралом (1) или частным решением в неявной форме, если при подстановки некоторого (одного) частного решения (1) уравнение (3) обращается в истинное тождество. Опр. 4 Конечное уравнение вида с произвольной постоянной С наз-ся общим интегралом уравнения (1), если при подстановки частного решения (1) при каком-либо значении С уравнение (4) обращается в истинное тождество. Замеч-ие. Определения (3) и (4) справедливы для уравнения первого порядка. Уравнение, правая часть которого является функцией линейного аргумента: y^/=f(ax+by+c), где a и b – постоянные, сводится к уравнению с разделяющимися переменными с помощью замены исходной переменной z=ax+by+c. Вычисляя производную от новой искомой функции z^/=a+by^/ и используя исходное уравнение, получаем: z^/=a+bf(z), откуда . Интегрируя, получим общий интеграл: , в котором осталось сделать обратную замену переменной z=ax+by+c.

2) Однородные дифференциальные уравнения первого порядка и приводящиеся к ним. Однородным называется уравнение, которое может быть представлено в виде: y^/=f(y/x) или: M(x,y)dx+N(x,y)dy=0, где M(x,y) и N(x,y) – однородные функции одинаковой степени однородности. Функция F(x,y) называется однородной степени n, если для любого t>0 выполняется тождество: F(tx,ty)≡tⁿF(x,y). Однородное уравнение сводится к уравнению с разделяющимися переменными с помощью замены искомой переменной z=y/x или y=xz. Дифференцируя указанную замену по x, получаем y^/=xz^/+z для первой формы однородного уравнения и dy=xdz+zdx для второй. Подставляя найденную производную в исходное уравнение, получаем уравнение с разделяющимися переменными: xz^/+z=f(z), или . Интегрируя, получаем общий интеграл: , в котором осталось сделать обратную замену переменной z=y/x. Уравнение с правой частью в виде функции дробно-линейного аргумента , где a₁, b₁, c₁, a₂, b_2, c₂ – постоянные, преобразуется в однородное уравнение с помощью введения новых переменных u и v по формулам x=u+x₀, y=v+y₀ (1), где x₀ и y₀ – решение системы линейных алгебраических уравнений a₁x+b₁y+c₁=0, a₂x+b₂y+c₂=0. Так как , то, подставляя (1) в исходное уравнение, получаем , то есть получаем однородное уравнение вида . Описанный метод неприменим в случае параллельности прямых (2). Но в этом случае коэффициенты в уравнениях (2) пропорциональны a₂/a₁=b₂/b₁=k, и исходное уравнение можно записать в виде , и заменой переменной z=a₁x+b₁y свести к уравнению с разделяющимися переменными.

3) Линейные дифференциальные уравнения первого порядка. Метод вариации постоянной. Линейным дифференциальным уравнением первого порядка называется уравне- ние линейное относительно неизвестной функции и ее производной. Линейное уравнение имеет вид: y^/+p(x)y=f(x) (1). Если f(x)≡0, то уравнение (1) называется линейным однородным. Для интегрирования неоднородного линейного уравнения применяется метод вариации постоянной, который состоит в следующем. Сначала интегрируется соответствующее однородное линейное уравнение y^/+p(x)dx, в котором переменные разделяются: , откуда, интегрируя, получаем , где С – произвольная постоянная. Решение исходного уравнения ищем в виде (2), где С(х) – новая неизвестная функция переменной х. Вычислим производную dy/dx: . Подставим ее и (2) в исходное уравнение (1): , после приведения подобных получаем , откуда, интегрируя, находим функцию и после ее подстановки в (2) получаем общее решение исходного уравнения: , где первое слагаемое – решение однородного уравнения, а второе слагаемое – частное решение. Т.о. решение линейного уравнения = решение соответствующего однородного уравнения (общего) +некоторое частное решение неоднородного уравнения (1).

4) Уравнения Бернулли и Риккати. Уравнение вида y^/+p(x)y=f(x)yⁿ, n≠1 (1) наз-ся уравнением Бернулли. 2 способа решения данного уравнения:1) заменой переменной z=y^1-n сводится к линейному уравнению. Умножим обе части (1) на y^-n(1-n), получим (2). Сделав замену z=y^1-n и подставив в (2), получим - линейное уравнение. 2) методом вариации постоянной. Сначала интегрируем соответствующее однородное уравнение y^/+p(x)y=0, в котором переменные разделяются: , откуда, интегрируя, получаем , где С – произвольная постоянная. Решение исходного неоднородного уравнения Бернулли ищем в виде (3), где С(х) – новая неизвестная функция переменной х. Вычисляя производную dy/dx и подставляя ее и (3) в исходное уравнение, после приведения подобных получаем - уравнение с разделяющимися переменными относительно неизвестной функции С(х), интегрируя которое, находим С(х) и после подстановки в (3) получаем общее решение исходного уравнения. Уравнение, имеющее вид y^/+p(x)y+q(x)y²=f(x) наз-ся уравнением Риккати. Если известно одно частное решение u(x) этого уравнения, то оно заменой y=u+z, где z(x) – новая неизвестная функция, сводится к уравнению Бернулли. Действительно, подставляя указанную замену в исходное уравнение, получим u^/+z^/+p(x)(u+z)+q(x)(u+z)²=f(x) или, учитывая, что u^/+p(x)u+q(x)u²≡f(x), после приведения подобных будем иметь уравнение Бернулли: z^/+(p(x)+2q(x)u(x))z = -q(x)z².

5) Уравнения в полных дифференциалах. Интегрирующий множитель. Уравнение, записанное в симметричной форме M(x,y)dx+N(x,y)dy=0 (1), называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции u(x,y) двух независимых переменных (она наз-ся потенциальной функцией уравнения (1)), то есть .du(x,y)=0, т.к. левая часть совпадает с правой частью (1). Предположим, что у = у(х) явл-ся решением (1). Тогда du(x,y(х))≡0u(x,y)=С (2), где С – произвольная постоянная. Т.о. мы получили конечное уравнение (2), определяющее все частные решения (1), но в неявной форме или получили общий интеграл уравнения (1). Для того чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие Эйлера: (3). Д-во.1)Необходимость. Предположим, что потенциальная функция уравнения (1) существует. Покажем, что в этом случае будет справедливо условие (3). . Т.к. в правых частях обеих последних формул дифференциалы dx, dy меняются независимо друг от друга, то совпадение правых частей возможнокогда коэффициенты при них совпадают, т.е. 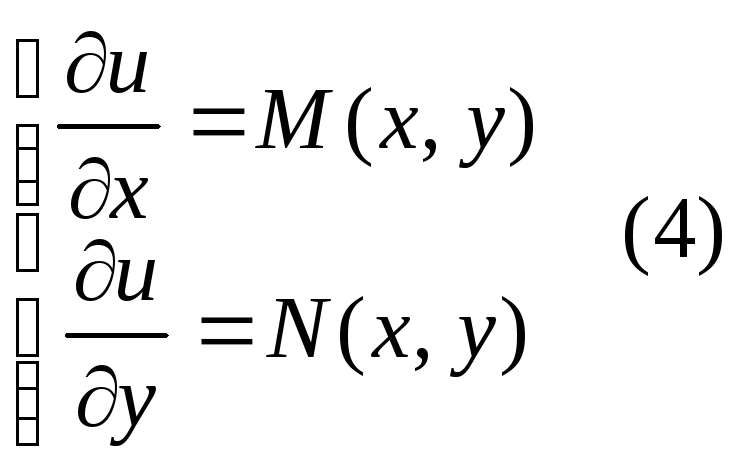. Продифференцировав первое равенство (4) по у, а второе по х, получим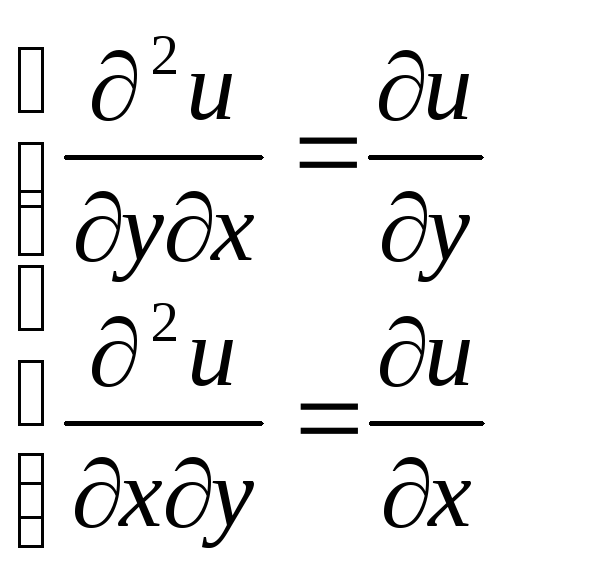. Достаточность. Предположим, что справедливо условие (3) . В этом случае гарантируется существование потенциальной функции. Для нахождения функции u(x,y) воспользуемся условием (4). Если потенциальная функция существует, то она должна удовлетворять (4) Интегрируя первое из равенств (4) по х (считая y постоянной), имеем (5), где φ(y) – произвольная функция от y. Дифференцируя полученное выражение по y и подставляя во второе из равенств (4), получаем . Последнее уравнение имеет смысл, а стало быть и решениеправая часть от х не зависит, а правая часть в силу условия Эйлера не зависит от х. Поэтому, интегрируя его по y, находим , подставляя результат в (5), получим искомую функцию . Вычислим от правой части (6) частную производную по х: . Т.к. правая часть (6) от х не зависит, значит достаточность доказана. Существует второй способ построения потенциальной функции: . Теорема. Криволинейный интеграл (7) при выполнении (3) не зависти от выбора пути интегрирования. Самой простой кривой, вдоль которой можно вычислить интеграл явл-ся ломаная, соединяющая наши 2 точки со звеньями, параллельными осям координат. В некоторых случаях, когда уравнение (1) не является уравнением в полных дифференциалах, удается подобрать функцию после умножения на которую левая часть уравнения (1) превращает в полный дифференциал . Такая функция называется интегрирующим множителем. Из определения интегрирующего множителя следует и условия Эйлера, следует что он должен удовлетворять уравнению , или или (8). В общем случае задача интегрирования этого уравнения в частных производных не легче, чем задача интегрирования уравнения (1), однако в некоторых частных случаях это уравнение упрощается и интегрирующий множитель μ легко находится. 1. Уравнение (1) имеет интегрирующий множитель, зависящий только от х. В этом случае уравнение (8) принимает вид . В этом уравнении левая часть является функцией только от x. Значит и правая часть должна быть функцией только от х, в противном случае интегрирующего множителя вида μ=μ(х) не существует. 2. Уравнение (1) имеет интегрирующий множитель, зависящий только от y. В этом случае уравнение (8) принимает вид . В этом уравнении левая часть является функцией только от y. Значит и правая часть должна быть функцией только от y, в противном случае интегрирующего множителя вида μ=μ(y) не существует. 3. Уравнение (1) имеет интегрирующий множитель μ=μ(z(x,y)), где z(x,y) – известная функция. В этом случае уравнение (8) принимает вид . 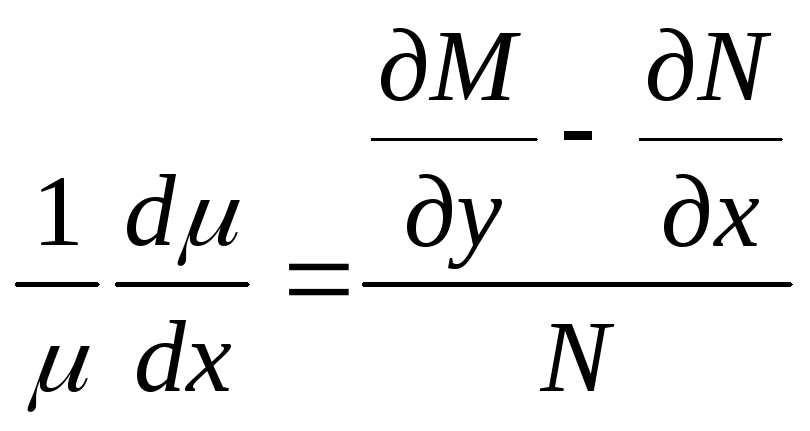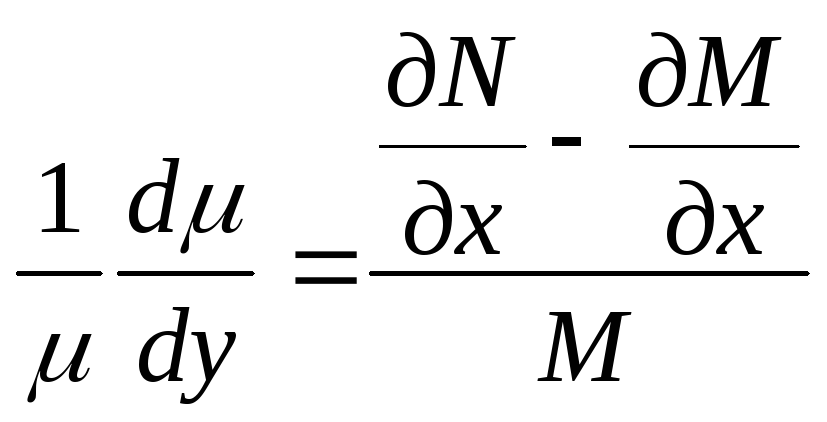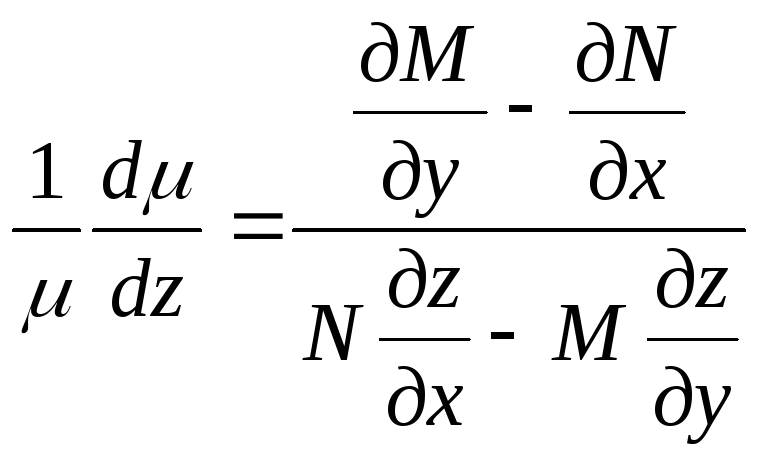В этом уравнении левая часть является функцией только от z. Значит и правая часть должна быть функцией только от z, в противном случае интегрирующего множителя вида μ=μ(z) не существует.

***********************************************************************************

7) Дифференциальные уравнения, не разрешенные относительно производной. Опр. 1 Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид F(x, у, у')=0 (1). В некоторых случаях (1) можно разренить относительно производной .Если это возможно, то получается одно либо несколько уравнений, уже разрешенных относительно производной: у' = f_i(х, у), где I = 1,2,…,каждое из которых решается отдельно подходящим методом интегрирования уравнения, разрешенного относительно производной. Объединяя решение каждого из этих уравнений, мы получим общее решение данного уравнения. Уравнение (1) разрешается относительно производной крайне редко. Даже если (1) можно разрешить относительно производной, то в результате такого разрешения можно получить настолько сложное уравнение, которое не удастся проинтегрировать. Опр. 2. Частным решением (1) в параметрической форме наз-ся 2 функции х иу, зависящие от t: , которые при подстановки в (1) обращают его в истинное тождество. При подстановке в (1) мы должны подставлять не только х у, но и у', т.е. .Опр. 3 Общим решением (1) в параметрической форме наз-ся совокупность всех его частных решений без исключения. Опр. 4 Если левая часть уравнения (1) не содержит независимой переменной х или искомой функции у, или того и другого вместе, то оно называется неполным. Рассмотрим некоторые из частных случаев. 1. Простейшим из неполных уравнений является уравнение, содержащее только производную: F(y') = 0. Общий интеграл такого уравнения находится следующим образом. Предположим, что это уравнение имеет некоторое (конечное или бесконечное) число вещественных корней y'=k_i, (i = l, 2, ...) (2), где k_i - некоторые постоянные, так что имеют место тождества: F(k_i)=0, (i=1,2,…) (3). Интегрируя уравнения (2), находим у = k_ix+С, откуда . После подстановки этого значения k_i в тождество (3) приходим к одному соотношению . Это соотношение и есть общий интеграл исходного уравнения. 2. Уравнение вида F(x, у')=0, не разрешенное относительно производной и не содержащее искомой функции, интегрируется методом введения параметра t и заменой исходного уравнения двумя уравнениями: x=φ(t), y^/=ψ(t). Для того, чтобы найти у через параметр t, воспользуемся основным тождеством диф. исчисления, который устанавливает связь м/у дифференциалом функции и ее производной. dy = y'dx, то в данном случае , откуда и, следовательно, общее решение исходного уравнения в параметрической форме определяется следующими уравнениями: , . 2а). Если исходное уравнение легко разрешимо относительно х: то удобно в качестве параметра ввести у' = t. Тогда , , . 3. Уравнение вида F(y,y')=0, не разрешенное относительно производной и не содержащее независи­мой переменной, также интегрируется методом введения параметра t и заменой исходного уравнения двумя уравнениями: , . Так как dy = y'dx, то в данном случае , откуда и, следовательно, общее решение исходного уравнения в параметриче­ской форме определяется следующими уравнениями: , . 3а). Если исходное уравнение легко разрешимо относительно у: , то удобно в качестве параметра ввести y'=t. Тогда , , . 4. Если уравнение f(z, у, у')=0 разрешимо относительно искомой функции, то есть приводится к виду y=f(x,у'), то, считая х и р = у' параметрами, получаем следующее пapaметрическое представление исходного уравнения: y=f(x,p), y^/=p. Для нахождения общего решения уравнения y=f(x,у') мы воспользуемся методом интегрирования с помощью дифференцирования. Продифференцируем обе части по х: то, учитывая, что у' = р, получаем уравнение, разрешенное относительно производной : . Интегрируя полученное уравнение (если оно интегрируется в квадратурах), получим Ф(х, р, С)=0. Совокупность уравнений Ф(х, р, С)=0, y=f(x,p) является общим решением исходного уравнения в параметрической форме. 5. Если уравнение F(x, у, у')=0 разрешимо относительно независимой переменной: x=f(y,y^/), то, считая у и р=у' параметрами, получаем следующее параметр кое представление исходного уравнения: x=f(y,p), y'=р. Воспользуемся методом интегрирования с помощью дифференцирования. Продифференцируем обе части по у: , и, учитывая, что у'=р, получаем уравнение, разрешимое относительно производной : . Интегрируя полученное уравнение (если оно интегрируется квадратурах), получим Ф{у, р, С)=0. Совокупность уравнений Ф(y,p,С)=0, x=f(y, р) является общим решением исходного уравнения в параметрической форме.

8) Уравнения Лагранжа и Клеро. Опр. 1 Уравнением Лагранжа называется линейное относительно х, у уравнение . Для интегрирования этого уравнения вводим параметр р = у'. Тогда (1). Дифференцируя по переменной х и полагая у'=р, получим , или . Это линейное относительно х и уравнение легко интегрируется, например, методом вариации постоянной. Найдя его общее решение х=χ(р,С) и присоединяя к нему соотношение (1), получаем общее решение ис­ходного уравнения в параметрической форме: х=χ(р,С) (2), . В процессе решения при делении на могут быть потеряны решения , при этом от (1) останется p=φ(p). Если оно имеет действительные корни р = р_i (i=l,2,…), то к ранее найденным решениям (2) и (3) можно добавить потерянное решение у = хφ(p_i)+ψ(p_i). Рассмотрим ситуацию, когда . Опр. 2 Уравнением Клеро называется частный случай уравнения Лагранжа: у = ху'+ψ(у^/). Для интегрирования этого уравнения вводим параметр р = у'. Тогда y = xp+ψ(p) (4). Воспользуемся метод интегрирования с помощью дифференцирования. Дифференцируя по переменной х и полагая у'=р, получим , или . Откуда или . В первом случае р=С и, исключая р из (4), получим: y=Cx+ψ(C) (5) - однопараметрическое семейство интегральных прямых. Во втором случае решение определяется двумя уравнениями x=-ψ^/(p), y=-pψ^/(p)+ψ(p) (6) в параметрической форме. Последние 2 уравнения явл-ся частным решением. Интегральная кривая, определяемая уравнениями (6) является огибающей семейства интегральных прямых (5). Опр. 3 Огибающей семейства кривых на плоскости, заданных уравнением Ф(х, у, С)=0 (7) наз-ся кривая , имеющая в каждой своей точке общую касательную с одной из кривых семейства. Уравнение определяет огибающую семейства (7), а уравнение определяет огибающую к (5).

9) Теорема существования и единственности решения дифференциального уравнения первого порядка, не разрешенного относительно производной. Особые решения. Рассмотрим диф. уравнение F(x, y, y') =0 (1); y(x₀) = y₀ (2) – начальное условие. Для уравнения (1) встает вопрос о единственности решения этого уравнения, удовлетворяющему условию (2). Понятие единственности решения этого уравнения понимается не так как для решения, разрешенного относительно производной (уравнения y' = f(x, y)). Уравнение (1) в принципе можно разрешить относительно y'. , i = 1, 2,… Если каждое из уравнений вида (3) удовлетворяет условию (2), то ч/з каждую точку (x_0, y₀) будет проходить только одна интегральная кривая уравнения (3). Под единственностью решения уравнения (1) мы будем понимать, что ч/з заданную точку (x_0, y₀) проходит одна интегральная кривая в заданном направлении. Теорема. Если в уравнении F(x, y, y') = 0 в некоторой замкнутой окрестности точки (x₀, y₀, y₀'), где y₀' – один из действительных корней уравнения F(x_0, y₀, y₀') = 0, функция F удовлетворяет условиям:1) F(x, y, y') непрерывна по всем аргументам; 2) ; 3) , то на отрезке x₀-h≤x≤ x₀+h, где h достаточно мало, единственное решение y=y(x) уравнения (1) удовлетворяющее начальному условию (2), для которого y'(x₀) = y₀'. Д-во. Из курса анализа по теореме о неявной функции выполнение первых двух условий нашей теоремы гарантирует существование единственной неявной функции y' = f(x, y)) (4); y'(x₀) = f(x₀, y₀), при этом функция f(x) будет непрерывна. При выполнении всех трех условий нашей теоремы у функции f(x) будет огранич. частн. производная по переменной у. Для того, чтобы а этом убедиться, воспользуемся теоремой о дифференцировании неявной функции, в которой при выполнении условий 1), 2), 3) гарантируется частной производной от нашей новой функции и она может быть найдена по правилу дифференцирования неявной функции. F(x, y, y') = 0. Продифференцируем обе части по у: . Т.о. второе условие теоремы о и единственности решения диф. уравнения, разрешенного относительно производной для уравнения (4) выполнено единственное решение (4), удовлетворяющее начальному условию (1) единственное решение (1). Особые решения. Опр.1 Точки на плоскости хОу, в которых нарушается свойство единственности уравнения (1) называются особым множеством уравнения (1).В точках этого множества должно нарушаться хотя бы одно из условий теоремы. В уравнениях, которые встречаются на практике условия 1), 3) нашей теоремы обычно выполняются , условие 2), где часто нарушается, Если 2) и 3) выполнены, то в точках особого множества должно выполняться: F(x, y, y') =0 и . Если из них исключить y', то мы получим , которому ложны удовлетворять точки особого множества. Опр. 2 Кривая на плоскости хОу, определяемая уравнением (5) наз-ся дискреминантной кривой уравнения (1). Не все точки дискр. кривой будут принадлежать особому множеству уравнения (1) , т.к. условия нашей теоремы явл-ся достаточными для единст-ти, но не явл-ся необходимыми, т.е. нарушение какого-либо из условий теоремы не обязательно влечет нарушение единственности решения. Опр. 3 Если какая-либо ветвь дискр. кривой (5) явл-ся интегральной кривой уравнения (1) или графиком одного из частных решений и при этом принадлежит особому множеству ур-я (1), то эта интегр. Кривая наз-ся особой интегральной кривой уравнения (1), а функция наз-ся особым решением уравнения (1). Т.о. для того, чтобы найти особое решение уравнения (1), необходимо:1)найти дискримин. кривую уравнения (1); 2)для каждой из ветвей дискримин. кривой проверить, является ли она интегр. кривой уравнения (1); 3)проверить нарушается ли в точках этой интегр. кривой единственность решения ур-я (1).