Дифуры ответы экзамен лето 2012

26) Однородные системы линейных дифференциальных уравнений. Основные свойства решений. Опр. 1 Система дифференциальных уравнений называется линейной, если она линейна относительно искомых функций х_i(t) и их производных. Линейная система n-го порядка, имеет вид , где а_ij(t) (i, j=1,2,…,n) в количестве n² штук наз-ся коэффициентами системы (1), f_i(t) (n штук) наз-ся правыми частями системы (1). Пусть , , , . Тогда в краткой векторной форме система (1) может быть записана в следующем виде . Если все коэффициенты а_ij(t), правые части f_i(t) системы (1) явл-ся непрерывными на отрезке , то система (1) на этом же отрезке удовлетворяет условиям теоремы о сущ-нии и един-ти решения. Дейст-но полные правые части системы (1) будут непрерывны по всем своим аргументам, т.к. они явл-ся линейными комбинациями. Существуют ограниченные частные производные от правых частей . Эти функции непрерывны, по т.Вейштрасса ограничены. Опр. 2 Если в системе уравнений (1) все правые части f_i(t)≡0 (i, j=1,2,…,n) или F(t)=0, то система (1) наз-ся линейной однородной. Линейная однородная система n-го порядка имеет вид или . Основные свойства частных решений:1)Если Х(t) явл-ся решением лин. однородной системы (2), то СХ(t), C=const также явл-ся решением (2). Д-во. ; 2)Если 2 векторные функции Х₁(t), Х₂(t) явл-ся решением одной и той же системы (2), то Х₁(t)+Х₂(t) тоже явл-ся решением (2). Д-во. ; 3) Если Х₁(t), Х₂(t),…,Х_m(t) явл-ся решением одной и той же системы (2), то линейная комбинация от этих функций с const явл-ся решением одной и той же cистемы.4)Если лин. однородная система (2) с действительными коэффициентами а_ij(t) имеет комплекснозначное частное решение X(t)=U(t)+iV(t), то вещественные и мнимые части этого решения по отдельности также явл-ся решением (2), Д-во. ; При подстановки должны получить тождество: . Две комплекснозначные функции тождественно совпадают у них совпадают тождественно вещественные и мнимые части .

27) Определитель Вронского линейной однородной системы уравнений и его основные свойства. Опр. 1 Х₁(t), Х₂(t),…,Х_n(t) наз-ся линейно зависимыми на отрезке , если и для выполняется . Опр. 2 Х₁(t), Х₂(t),…,Х_n(t) наз-ся линейно независимыми на отрезке , если для них тождество (1) выполняется, когда . Опр. 3 Х₁(t), Х₂(t),…,Х_n(t) функциональный определитель , где называется определителем Вронского. Свойства: 1)Если Х₁(t), Х₂(t),…,Х_n(t) являются линейно зависимыми на , то W(t)≡0 для . Д-во. По определению линейной независимости . Это векторное тождество эквивалентно скалярным тождествам . Относительно постоянных а_i система (2) явл-ся линейной однородной алгебраической системой ур-ний, определитель которой совпадает с определителем Вронского (W(t)). Система (2) имеет нетривиальное решение при t. Лин. однор. Система урав-ний имеет нетривиальное решение определитель = 0 W(t)≡0 . 2) Если Х₁(t), Х₂(t),…,Х_n(t) явл-ся линейно независимыми на частными решениями одной и той же линейной однородной системы с непрерывными коэффициентами на а_ij(t), то W(t)≠0 . Д-во. (от противного) : W(t₀)=0. Составим вспомогательную систему уравнений . Система (4) явл-ся линейной однородной алгебраической системой ур-ний; W(t₀)=0. Система (4) имеет ненулевое решение(по теореме) возьмем из этих ненулевых решений . . По свойству 3) частных решений линейной однородной системы Х(t) явл-ся решением системы (3). В силу (4) наше решение X(t₀)=0. С другой стороны, очевидно, что (3) имеет тривиальное решение ; . При сформулированных условиях (3) удовлетворяет условиям теоремы существования и единственности решения одно решение, удовлетворяющее начальному условию нулевому, т.е. противоречит независимости. В свойстве 2) дополнительное условие нашей функции явл-ся частным решением одной и той же лин. однор. системы (3) с непрерывными коэффициентами, Избавиться от дополнительного условия нельзя.

31) Неоднородные системы линейных дифференциальных уравнений. Общее решение. Принцип суперпозиции. Опр. 1 Система дифференциальных уравнений называется линейной, если она линейна относительно искомых функций х_i(t) и их производных. Линейная система n-го порядка, имеет вид , где а_ij(t) (i, j=1,2,…,n) в количестве n² штук наз-ся коэффициентами системы (1), f_i(t) (n штук) наз-ся правыми частями системы (1). Пусть , , , . Тогда в краткой векторной форме система (1) может быть записана в следующем виде . Соответствующая линейная однородная система n-го порядка имеет вид или . Свойства линейной неоднородной системы: 1)Если явл-ся решением лин. неоднородной системы, Х₀(t) явл-ся решением лин. однородной системы, то явл-ся решением лин. неоднородной системы. Д-во. . 2)Принцип суперпозиции. Решением системы линейных уравнений , является сумма , решений систем уравнений . Д-во. . Теорема (об общем решении линейной неоднородной системы уравнении). Общее решение линейной неоднородной системы (1) n-го порядка с непрерывными на отрезке [а,b] коэффициентами а _{i j} (t) (i, j=1,2,…,n) и правыми частями f_i(t) равно сумме общего решения соответствующей однородной системы и какого-либо частного решения рассматриваемой неоднородной системы. Д-во. - общее решение системы (1). Надо доказать: (3) – решение (1). То, что (3) явл-ся решением (1) следует из первого свойства частных решений. Нам нужно доказать более сильное утверждение: (3) – общее решение (1), т.е. оно содержит в себе все частные решения (1) без исключения. Т.к. в сформулированных условиях система 1) удовлетворяет условиям теоремы сущест. и единств. реш-я, то нам достаточно показать, что постоянные с_i в решении (3) всегда можно подобрать таким образом, чтобы (3)удовлетворяло Х(t₀) = Х₀ (4), где . Для того, чтобы убедиться, подставим в (3) начальные условия (4): . Система ур-ний (5) относительно с_i явл-ся линейной неоднородной системой ур-ний, определитель которой = определителю Вронского - W(t₀). По второму свойству определителя Вронского W(t₀)≠0, т.к. функции линейно независ. частные решения (2) по теореме Кронекера-Копелли система (5) имеет имеет решение при правых частях и при .

32) Неоднородные системы линейных дифференциальных уравнений. Метод вариации постоянных. Опр. 1 Система дифференциальных уравнений называется линейной, если она линейна относительно искомых функций х_i(t) и их производных. Линейная система n-го порядка, имеет вид , где а_ij(t) (i, j=1,2,…,n) в количестве n² штук наз-ся коэффициентами системы (1), f_i(t) (n штук) наз-ся правыми частями системы (1). Пусть , , , . Тогда в краткой векторной форме система (1) может быть записана в следующем виде . Соответствующая линейная однородная система n-го порядка имеет вид или .Построение общего решения линейной неоднородной системы уравнений осуществляется в 2 этапа: 1)находится общее решение соответствующей линейной однородной системы(2); 2)подбирается какое-нибудь одно решение системы (1). Метод подбирания частного решения: предположим, что обще решение найдено, а подобрать частное е можем. Тогда общее решение (1) может быть получено методом вариации постоянных: пусть известны - общее решение (2); X(t) – общее решение (1) будем искать в форме . Для того, чтобы найти С_i(t), подставляем (3) в (1): , F_i – частное решение (2) ; . Относительно (4) – линейная неоднородная алгебраическая система, определитель которой = ≠0 – ФСР соответствующей (2) (4) по теореме Кронекера-Копелли имеет единственное решение при правых частях (второй индекс указывает на номер решения, первый – номер неизвестной функции) подставляем в (3) и находим искомое решение. Метод вариации постоянных является универсальным.

33) Неоднородные системы линейных дифференциальных уравнений с постоянными коэффициентами. Метод неопределенных коэффициентов. Опр. 1 Система дифференциальных уравнений называется линейной, если она линейна относительно искомых функций х_i(t) и их производных. Линейная система n-го порядка, имеет вид , где а_ij(t) (i, j=1,2,…,n) в количестве n² штук наз-ся коэффициентами системы (1), f_i(t) (n штук) наз-ся правыми частями системы (1). Пусть , , , . Тогда в краткой векторной форме система (1) может быть записана в следующем виде . Соответствующая линейная однородная система n-го порядка имеет вид или . Частное решение системы (1) может быть найдено методом неопределенных коэффициентов:1)позволяет находить частные решения (1); 2)не является универсальным. Условия принимаемости:1)все коэффициенты – const; 2)все правые части – правые части специального вида, к ним относятся произведения показательных функций на многочлен, произведения показательных функций на сумму, произведения sin, cos на многочлен, суммы функций этих двух видов. Применим алгоритм сведения системы уравнений к одному уравнению высокого порядка уравнений для линейной неоднородной системы с постоянными коэффициентами и специальными правыми частями:1)произведем почленное дифференцирование обеих частей; 2)из правой части полученного уравнения исключаем правые от искомой функции; 3)Эта система уравнений решалась относительно исключенной функции. Эта система уравнений линейна.; 4)

После применения этого алгоритма получим уравнение с одной искомой функцией (линейное с коэффициентами – константами и с правой частью специального вида). Метод неопределенных коэффициентов для (1):1) , где многочлен - степени m_i, где р – постоянная, называемая контрольным числом правых частей (единое для всех), тогда частное решение (1) нужно искать в форме , где - мн-н степени m+r с неопределенными коэффициентами, . Число r=0, если р не явл-ся корнем характеристического уравнения, если же p явл-ся корнем характеристического уравнения, то r = кратности этого корня. Чтобы найти коэффициенты многочленов , надо решение (4) подставить в исходную систему (1) и приравнять коэффициенты при подобных членах в левых и правых частях уравнений, в результате чего получим систему линейных алгебраических уравнений относительно искомых коэффициентов.2) Если каждая из правых частей неоднородной системы (1) представима в виде ,

где - многочлены, то неоднородная система имеет частное решение вида , где - многочлены с неопределенными коэффициентами степени m+r, m = наибольшей из степеней многочленов . Число r=0, если контрольное число р+iq не явл-ся корнем характеристического уравнения; если р+iq является корнем характеристического уравнения, то г = кратности этого корня. Чтобы найти коэффициенты многочленов , надо решение (6) подставить в исходную систему и приравнять коэффициенты при подобных членах в левых и правых частях уравнений получим систему линейных алгебраических уравнений относительно искомых коэффициентов.

Если из правы части (1) равны суммам нескольких функций вида (3) и (5) или разнотипным функциям вида (3) и (5), то частное решение (1) находится при помощи принципа суперпозиции: частное решение (1) с правыми частями равно сумме частных решений соответствующих систем с правыми частями, равными каждому из наборов функций .

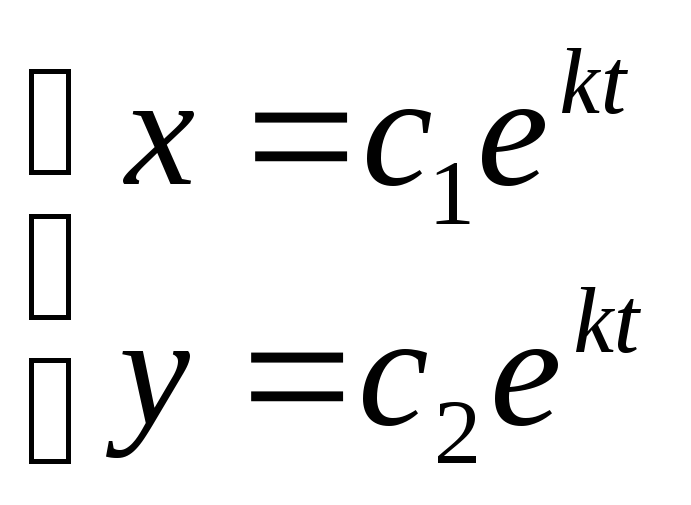
36) Понятие устойчивости. Простейшие типы точек покоя (случай кратных корней характеристического уравнения, вырожденные случаи). 1) . Рассмотрим 1а) 2 линейно независимых собственных вектора матрицы А р = n-rang(A-kE)=2; rang(A-kE)=0 A=kE система (1) примет вид - распавшаяся система уравнений. y=Cx, т.е. фазовый портрет имеет лучи. 1а^-) k<0. Точка покоя явл-ся устойчивой точка покоя асимптотически устойчивая. Такой фазовый портрет наз-ся устойчивым дикритическим узлом. 1а⁺) k>0. Точка покоя покинет ε-окрестностьточка покоя неустойчива. Фазовый портрет наз-ся неустойчивым дикритическим узлом. 1б) B₁ – собственный вектор, B₂ – присоединенный вектор, порожденный собственным. Общее решение , где. Применим к исходной фазовой плоскости Р аффинное преобразование, которое переводит Р в вспомогательную плоскость , в которой B₁ и B₂ переходят в 2 взаимоортогональных единичных вектора. 1б^-) k<0. Если у С₁ и С₂, то мы получим новую фазовую траекторию системы (1), расположенную симметрично относительно начала координат по отношению к исходной траектории, заданной (3). Т.о. картина фазовых траекторий обладает симметрией относительно начала координатдостаточно построить фазовые траектории плоскости только в верхней полуплоскости. С₂>0 (т.к. в верхней полуплоскости); убывает к 0. При достаточно больших по модулю, неотрицательных t С₁+С₂t>0. Точка покоя явл-ся устойчивой. Т.к. точка покоя явл-ся асимптотически устойчивой. Такой портрет наз-ся устойчивым вырожденным узлом. 1б⁺) k>0. Точка покоя неустойчива. Фазовый портрет наз-ся неустойчивым вырожденным узлом. Сделаем аффинное преобразование из в . 2)k=0. В этом случае нарушается условие единственности точки покоя. 2а) . Если С₁=0, то все точки оси η неподвижны, они явл-ся точками покоя. Если С₁≠0, то:2а^-) ξ убывает и движение направлено к центру. Все точки покоя устойчивы, но неасимптотически. 2а⁺) ξ возрастает и движение направлено от центра.Все точки покоя будут неустойчивы. 2б) Существует 2 линейно независимых собственных вектора(частный случай 1а)) . Вся плоскость Р состоит из точек покоя, они все устойчивые, но неасимптотически. 2в) . Существует 1 собственный вектор B₁ (частный случай 1б)) . Если С₁=0, то все точки прямой ξ – точки покоя.. С₂≠0, то они неустойчивы.

41)Линейные и квазилинейные уравнения в частных производных первого порядка. Опр. 1 Квазилинейным уравнением первого порядка в частных производных наз-ся ур-ние вида , где - функции, определенные в некоторой области переменных (X, z). Опр. 2 Уравнение (1) является линейным относительно производных от функции z и линейным относительно самой функции z , т.к. коэффициенты уравнения от искомой функции зависят и правая часть тоже. Если в уравнении (1) правая часть ≡ 0 , а все коэффициенты левой части не зависят от функции z, то уравнение (1) – линейное однородное. . Рассмотрим квазилинейное уравнение с двумя независимыми переменными. Функция z зависит от двух переменных z=z(x, y), тогда квазилинейное уравнение примет вид . Рассмотрим векторную функцию . Функции P,Q,R непрерывны в той области, в которой мы будем их рассматривать. Опр.3 Пространственная линия, касательная к которой ее точке параллельна вектору в этой же точке наз-ся векторной линией этого поля F Опр.4 Поверхность, составленная из векторных линий поля F наз-ся векторной поверхностью поля F. - вектор бесконечно малой касательной, . Система (4) явл-ся системой обыкновенных диф. ур-ний, записанная в симметричной форме векторную поверхность можно рассматривать как состоящую из семейства векторных линий, непрерывно зависящих от одного параметра, т.е. одно параметрическое семейство векторных линий поверхность в пространстве можно определить, задав вектор нормали к этой поверхности как функцию координат точек этой самой поверхности. z=f(x, y); ; . Т.о. задача нахождения векторных поверхностей поля F эквивалентна задаче нахождения решения квазилинейного уравнения (3). Предположим, что искомая векторная поверхность задается неявным уравнением u(x, y ,z)=0 и квазилинейное уравнение примет вид . Задача нахождения общих решений уравнения (3) и (6) эквивалентны. (6) – линейное однородное уравнение. В уравнении (3) количество независимых уравнений = 2, а в (6) их 3.. В дальнейшем будем рассматривать уравнение (3) и все будет справедливо для(6). Ур-ние (3) определяет все векторные поверхности поля F , но из этих векторных поверхностей состоит из векторных линий того жнее самого поля. Эти векторные линии определяются системой уравнений (4)обыкновенных диф. ур-ний, записанных в симметричной форме. Пусть - 2 независ. первых интеграла системы (4). Опр. 5 Ур-ние (7) в пространстве переменных x, y, z определяют линии, которые наз-ся интегр. линиями системы ур-ний (4) или характеристиками уравнения (3) (или(6)). Эти лини заполняют пространство целиком. Т.к. наши линии зависят от двух переменных, то они образуют двухпараметр. семейство. Для того, чтобы из двухпараметр. семейства (7) получить однопараметр. сем-во(поверхность), нужно избавиться от лишнего параметра. Пусть Ф(с₁, с₂)=0 – произвольная диф. функция. Подставляя (7) в последнее ур-ние, получим . Ур-ние (8) будет определять общее реш-ие (3) в неявной форме. Встречается и другая задача: найти векторную поверхность поля F , проходящую через заданную линию в пространстве. Пусть заданная линия имеет вид . Для того, чтобы получить конкретную функцию Ф, нужно объединить (7) и (9) . Система из четырех уравнений. Из нее исключаем x, y, z Ф(с₁, с₂)=0, где Ф – конкретная. Воспользовавшись этой функцией и (8), получим вектор. повер-ть, проходящую ч/з линию, определяемую (9). Эта поверхность наз-ся интегральной поверхностью (3)или (6).Т.о. чтобы найти общее реш-ие (3) или(6), нужно:1)Составить вспомогательную систему обыкновенных диф. ур-ний.; 2)найти 2 независимых первых интеграла этой системы; 3)Выписываем общее решение в виде (8). Если нужно найти ту интегр. поверх-ть (3)или(6), которая проходит ч/з заданную линию (9), то из четырех ур-ний 7) и 9) исключаем x, y. z и получаем конкретное уравнение, связывающее 2 параметра с₁, с₂ Ф(с₁, с₂)=0; 4)Подставляя в это ур-ние вместо с₁, с₂, левые части (7) получим ур-ние искомой поверх-ти. Если во второй задаче линия, определяемая (9), явл-ся характеристической ур-ния (3) или(6) наша задача неопределенна бесконечно много решений.