Формула Остроградского-Лиувилля.

Т :Пусть есть

с непререрывными коэффициентами

Если у этих уравнений общая фундаментальная система решений , то (7) и(21) совпадают,

Док-во

Вычитаем из (7) (21):

У (22) хотя бы в одной точке

хотя бы один из коэффициентов .

То т.к. непрерывны этот коэффициентв некоторой окрестности точки.То в этой окрестностиуравнение(22) будет линейным, однор, порядка не вышеn-1,

у которого частное решение.

Согласно тому что, макс. число лин. нез. частных решений лин. однор. уравнения равно его порядку, то частных решений на одно больше. Противоречие. (7) и (21) совпадают.

Таким образом, ф.с.р. однозначно определяет лин. однор. уравнение.

Поставим задачу: построить лин, однор, диф, уравнение имеющее решение .Т.к,искомого уравнения будет лин. зависеть от ф,с,р, тоn+1 функция будет лин.зависимой. То по 1 св-ву опеделителя Вронского

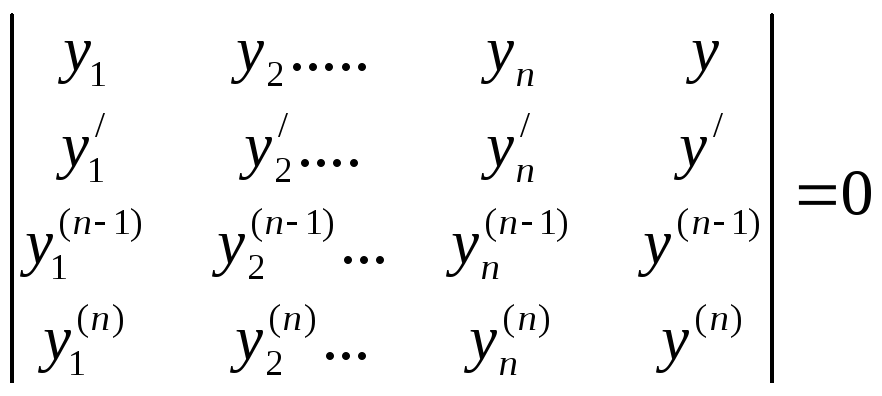Разложим по последнему столбцу:

Првило диф. определителя: производная от определителя= сумме n определителя (первый получается путем диф. первой строки, второй- диф. второй сторки, последний- диф. последней сторки).Применяя это правило к определителю Вронского- все слагаемые кроме последнего

-ф.с.р. лин. однор. уравнения, частное решение, лин. нез.То по 2 св-ву определителя Вронского

- искомое.

Если сравнить (23) с (7) -уравнение 1 порядка с раздел. переменными, кот. интегрируется:

потенцеируем:

(24)- формула Остроградского-Лиувилля. Может использоваться для понижения порядка лин. однор. уравнения, если извнестно решение: .

Понизим его порядок, то согласно (24):

Это уравнение может быть решено методом вариаций постоянной, но применим метод интегрирующего множителя.

.Умножим на M.

Интегрируем по х.

Получим

№22

Краевая задача для дифференциального уравнения второго порядка. Функция Грина.

Чтобы можно было использовать диф. уравнения для мат. моделирования какого-либо процесса, необходимо к диф. уравнению добавить дополнительные условия(чаще начальные условия).Задача нахождения частного решения диф. уравнения, кот. удовлетворяет начальным условиям, наывается задачей Коши. Термин нач. условия означает, что допустимые условия на искомую функцию и ее производные задаются в одной и той же точке. Типичный пример этого рода задачи- баллистический пример. Если общее решение диф. уравнения уже найдено, то для нахождения решения краевой задачи подставь дополнительные условия(краевые).

Опр: Краевой задачей для уравнения(1) наз. задача нахождения такого частного решения ур. (1), которое удовлетворяет двум краевым условиям.

Краевые условия наз. краевыми условиями 1 рода, если на концах отрезка задаются значения искомой функции, т.е.

Если в концахзадаются

, то краевыми условиями 2 рода.

Краевые условия наз. краевыми условиями 3 рода(смешенными), если на концах отрезка задаются лин. комбинации функции и ее производной

Краевые условия 1 рода можно свести к однородным краевым условиям. Дя этого надо сделать замену:

Краевые условия однородны:

Поэтому не ограничивая общности дальнейших рассуждений будем считать, что наши краевые условия однородны.

Необходим способ решения задач, кот. не требует нахождения общего решения ур(1)(т.к. это удается крайне редко).Такой способ существует он связан с функцией Грина.

Опр: Функцией Грина на краевой задачи (1)(5) наз. функция двух переменных G(x,s)

которое удовлетворяет:

1)Функция Грина кромеx=s является решением соответствующего лин. однор. уравнения.

2) функция Грина удовлетворяет условиям(5)

3)функция Грина непрерывна по х.

4)кромеx=s непрерывна, x=s эта производная терпит разрыв и величина скачка равна.

Если функция Грина для краевой задачи (1)(5)известна, то решение этой краевой задачи находится по формуле:

.

Докажем что (7) является решением краевой задачи(1)(5).

Краевые условия выполняются в силу условия (2) для функции Грина, т.к. опр. интеграл от нулевой фун. равен 0. Проверим, что (7) удовлетворяет (1).

Вычисляем

Для вычисления второй производной применим теорему о диф. интеграла с переменным верхним пределом или нижним пределом.

При подстановке (7) в (1) получим верное тождество.

Для построения функции Грина берем любое частное решение соотетствующего уравнения (6) которое удовлетворяет(1) условию (5):, но не удовлетворяет (2)

.По первому св-ву частных решений лин. однор. уравнений функция -частное решение (6), при любомудовлетворяет 1 условию (5)бно не удовл. (2), прине удовл. 2 условию (5)

удовл.

не удовл.

-частное решение ур. (6)

удовлетворяет 2 при , не удовл 1

1)Т.к. ,явл. решением (6), то функция Грина тоже явл. решением (6), кроме точкиx=s.

2) Очевидно, что 2 краевые условия

совпадают с определителем Вронского

Функции -решения (6)-лин.нез. на,т.к. если

то , то по 2 св-ву Определителя Вронского

Подставим.

№37

Понятие устойчивости. Теорема Ляпунова об устойчивости.

Т1:(Ляпунова об устойчивости)

Если существует диф. функция ,которая называется функцией Ляпунова в некоторой окрестности нач. координат удовлетворяет:

1)

2)

то системы (1) является устойчивым. Производная вдоль фазовой траектории системы (1) вычисляется так: вместоподставляем

ситемы (1) .В результате v превращается в сложную функцию параметра i.

Чтобы док-во было более понятным и наглядным я иск. геометрическую интерпретацию.

Опр: Поверхностью уровня фунуции многих переменных наз. гиперповерхность в n- мерном пространстве на которой функция v принимает const значенияе.

Иллюстрации будут в двумерном пространстве, но это будет справедливо в размерности 3.

Поверхности уровня функции Ляпунова

будут замкнутыми поверхностями вложенными друг в друга и содержащими начало координат.

Рисунок.

Все поверхности замкнуты

Рисунок.

Поверхность не проходит через начало координат.

V<C

Возьмем любую m в окрестности в качестве начальной точки некоторой фазовой траектории.

Вычислим Значение функции Ляпунова.

начального значения.

По определению устойчивости точка покоя явл. устойчивой по Ляпунову .ч.т.д.

№39