Раздел 1
		Методы исследования систем управления

1.1. Метод линейного программирования

Большое число экономических задач сводится к линейным математиче­ским моделям. Традиционно их называют моделями линейного программиро­вания. Под линейным программированием понимается линейное планирование, т.е. получение оптимального плана-решения в задачах с линейной структурой. Обычно его используют специалисты штабных подразделений для разрешения производственных трудностей. Типичными примерами применений модели линейного программирования являются следующие:

• укрупненное планирование производства (составление графиков производства, минимизирующих общие издержки в связи с изменением ставки процента);

• планирование ассортимента изделий (определение оптимальной структуры производства продуктов питания для человека);

• маршрутизация производства изделий (определение оптимального технологического маршрута изготовления изделия);

• регулирование запасов (определение оптимального сочетания продуктов на складе);

• календарное планирование производства (составление календарных планов, минимизирующих издержки с учетом расходов на содержание запасов, оплату сверхурочной работы и заказов на стороне);

• планирование распределения продукции и пр.

В самом общем виде линейное программирование сводится к оптимизационной задаче и записывается в следующем виде:

где	Х = (х1,х2,…,хп); W – область допустимых значений переменных х1,х2,…,хп; f(X) – целевая функция.

Чтобы решить задачу оптимизации, достаточно найти ее оптимальное решение, т.е. указать такое, чтоf(X₀)≥ f(X) при любом , или для случая минимизации -f(X₀)≤ f(X) при любом .

Оптимизационная задача является неразрешенной, если она не имеет оптимального решения. В частности, задача максимизации будет неразрешенной, если целевая функция f(X)не ограничена сверху на допустимом множестве W.

Методы решения оптимизационных задач зависят как от вида целевой функции f(X), так и от строения допустимого множества W. Если целевая функция в задаче является функцией п переменных, то методы решения называются методами математического программирования.

Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:

		(1)
		(2)
		(3)
		(4)

При этом система линейных уравнений (2) и неравенств (3), (4), определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция f(X) называется целевой функцией, или критерием оптимальности.

Если математическая модель задачи линейного программирования имеет вид:

		(5)
		(6)
		(7)
		(8)

то говорят, что задача представлена в канонической форме.

Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме, переводя максимизацию к минимизации, от ограничений неравенств к ограничениям равенств и заменяя переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком и наоборот.

Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:

1) если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;

2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на (-1);

3) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных, они преобразуются в равенства;

4) если некоторая переменная x_k не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными: x_k=x’_k-x₁, где 1 – свободный индекс, x’_k≥0, x₁≥0.

Обобщая сказанное можно сделать следующие выводы:

1. Ограничения в задачах линейного программирования могут быть выражены как равенствами, так и неравенствами.

2. Линейная функция может стремиться как к максимуму, так и к минимуму.

3. Переменные в модели всегда неотрицательны.

4. От любой задачи линейного программирования можно перейти к канонической (основной) задаче линейного программирования.

Каждой задаче линейного программирования можно противопоставить другую задачу линейного программирования, двойственную по отношению к исходной (прямой).

Рассмотрим задачу линейного программирования следующего вида:

		(9)
	………………………..	(10)

В задаче требуется максимизировать целевую функцию; все ограничения являются неравенствами со знаком ≤, все переменные х₁, х₂,…,х_п неотрицательны. Задача содержит п управляющих переменных и m ограничений. Коэффициенты при переменных в целевой функции: c₁, c₂,…,c_n; свободные члены: b₁, b₂,…,b_m.

Двойственная задача линейного программирования имеет вид:

		(11)
	………………………..	(12)

В двойственной задаче требуется найти минимум целевой функции, ограничения – неравенства со знаком ≥, управляющие переменные y₁, y₂,…,y_m неотрицательны. Задача содержит m управляющих переменных и n ограничений. Коэффициенты целевой функции задачи b₁, b₂,…,b_m являются свободными членами исходной задачи линейного программирования, а свободные члены двойственной задачи c₁, c₂,…,c_n – коэффициентами целевой функции исходной задачи линейного программирования. Матрица коэффициентов двойственной задачи транспонирована, т.е. строки заменены столбцами, а столбцы – строками.

Задачи (9) –(10) и (11) – (12) образуют пару задач, называемую в линейном программировании двойственной парой.

Двойственная задача по отношению к исходной составляется по следующим правилам:

1. Целевая функция исходной задачи задается на максимум, а целевая функция двойственной – на минимум.

2. Матрица А (13)

,

(13)

составленная из коэффициентов при неизвестных в системе ограничений (10) исходной задачи (9) – (10) и аналогичная матрица в двойственной задаче (11) – (12) получаются друг из друга транспонированием.

3. Число переменных в двойственной задаче (11) – (12) равно числу ограничений в системе (10) исходной задачи, а число ограничений в системе (12) двойственной задачи – числу переменных в исходной задаче.

4. Коэффициентами при неизвестных в целевой функции (11) двойственной задачи являются свободные члены в системе (10) исходной задачи, а правыми частями в ограничениях системы (12) двойственной задачи - коэффициенты при неизвестных в целевой функции (9) исходной задачи.

5. Если переменная x_j исходной задачи (9) –(10) может принимать только лишь неотрицательные значения, то j-е ограничение в системе (12) двойственной задачи является неравенством вида ≥. Если же переменная x_j может принимать как положительные, так и отрицательные значения, то j-е ограничение в системе (12) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (10) исходной задачи и переменными двойственной задачи. Если i-е ограничение в системе (10) исходной задачи является неравенством, то i-я переменная двойственной задачи y_i≥0. Если же i-е ограничение есть уравнение, то переменная y_i может принимать как положительные, так и отрицательные значения.

Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программирования – симплекс-метода. Геометрический смысл этого метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере, не худшее) значение (по отношению к цели задачи) до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум). Идеи метода были опубликованы российским ученым Л.В. Канторовичем в 1939 г.

Для применения симплекс-метода в ограничения задачи вводятся дополнительные переменные y₁, y₂,…,y_i и условие исходной задачи принимает вид:

	……….…………………..	(14)

Эту постановку можно представить в виде таблицы – первой таблицы симплекс-метода (табл. 1.1).

Таблица 1.1.

Первая симплекс-таблица

Базис	Свободные члены	Свободные переменные
		x1	x2	…	xn
y1	b1	a11	a12	…	a1n
y2	b2	a21	a22	…	a2n
…	…	…	…	…	…
ym	bm	am1	am2		amn
Индексная строка	0	-c1	-c2	…	-cn

Для составления симплекс-таблицы можно применить определенные правила.

1. Для первой таблицы:

а) в первый столбец записывают y_m – базисные переменные, которые находятся в уравнениях слева;

б) свободные переменные a_mn выносят в верхнюю строку таблицы;

в) в остальные столбцы записывают коэффициенты перед свободными переменными.

2. Для последующих таблиц:

а) выбирается наименьший отрицательный элемент в индексной строке при отыскании максимума, но наибольший положительный – при отыскании минимума, исключая вектор свободных членов;

б) этот элемент определяет ключевой вектор-столбец и он вводится в базис;

в) компоненты вектора свободных членов делятся на положительные элементы ключевого столбца;

г) из полученных отношений выбирается наименьшее;

д) вектор-строка, содержащая наименьшее положительное частное - ключевая и выводится из базиса;

е) на пересечении ключевых строк и столбца находится разрешающий элемент;

ж) преобразование матрицы:

- каждый элемент ключевой строки делится на разрешающий элемент. Полученные частные являются элементами ключевой строки следующей таблицы,

- ключевой столбец в новой таблице – нули, за исключением разрешающего элемента,

- остальные элементы новой таблицы рассчитываются по схеме:

Новый элемент = Старый элемент –

- Элемент ключевой строки*Элемент ключевого столбца

Разрешающий элемент

- если нулевая строка (столбец) содержит нуль, то соответствующий столбец (строка0 в новой таблице не изменится.

3. Пункты «а» - «ж» повторяются до тех пор, пока в индексной строке не останется ни одного отрицательного элемента при отыскании максимума (но ни одного положительного при отыскании минимума).

Пример 1.1. Требуется принять решение об оптимальном плане производства трикотажа на месяц на ОАО «Свияж» с применением симплекс-методы.

Определим план выпуска моделей мужского трикотажа с целью получения максимальной прибыли при заданных ресурсах с помощью построения математической модели. Исходные данные представлены в таблице 1.2.

Таблица 1.2.

Исходные данные

Ресурсы (i)	Вид продукции (j)				Запас ресурса (bi)
	Брюки спортивные модель 7060	Свитер мужской модель 55-1	Джемпер мужской модель 38-0	Костюм спортивный модель 1246-0
	удельный расход ресурса (aij)
Трудовые	4,95	5,06	4,88	4,66	170000
Материальные	7,90	27,97	55,50	29,83	1050000
Оборудование	1,65	3,37	3,05	2,33	120000
Прибыль	16	112	222	38	-
План	x1	x2	x3	x4	-

Исходные данные по удельному расходу материальных, трудовых ресурсов проставлены в табл. 1.2 в соответствии с действующей в организации нормативной и технологической документацией. По строке «Материальные ресурсы» зафиксирована норма расхода наиболее дефицитного (лимитируемого0 вида материалов – пряжа шерстяная. Этот материал имеет самую высокую норму расхода и стоимость.

По строке «Оборудование» проставлена сводная трудоемкость изготовления единицы изделия в нормо-часах как суммарная по всем детале-операциям. Остальные виды ресурсов также взяты в натуральных единицах: трудовые ресурсы – в часах; материальные – в дм².

Строка «Прибыль» отражает прибыль от реализации единицы изделия, взята в из плановой калькуляции на единицу изделия.

Через x₁,x₂,x₃,x₄ обозначили количество выпускаемой продукции каждого вида ассортимента.

Согласно правилу построения стандартной задачи линейного программирования составим математическую модель:

(15)

В ограничениях задачи введем дополнительные переменные y₁, y₂, y₃ и перепишем условие задачи в виде уравнения:

(16)

Последнюю постановку можно представить в виде таблицы 1.3 – первой таблицы симплекс-метода, которой воспользуемся для решения задачи линейного программирования.

Таблица 1.3.

Первая симплекс-таблица

Базис	Свободные члены	Свободные переменные
		x1	x2	x3	x4
y1	170 000	4,95	5,06	4,88	4,66
y2	1 050 000	7,90	27,97	55,50	29,83
y3	120 000	1,65	3,37	3,05	2,33
Индексная строка	0	-16	-112	-222	-38

В первый столбец записаны y_i –базисные переменные, которые находятся в уравнении слева, а свободные переменные x_j вынесены в верхнюю строку таблицы. В остальных столбцах записаны коэффициенты перед свободными переменными. Индексная строка – результат вычитания из нуля коэффициентов перед свободными переменными.

Для построения следующей таблицы выбирается наименьший отрицательный элемент в индексной строке (это 222). Этот элемент определяет ключевой вектор-столбец и он вводится в базис. Компоненты вектора свободных членов делятся на положительные элементы ключевого столбца и из полученных отношений выбирается наименьшее. Вектор-строка, содержащая наименьшее положительное частное, - ключевая и выводится из базиса (y₂). На пересечении ключевых строк и столбца находится разрешающий элемент (это 55,50).

Затем каждый элемент ключевой строки делится на разрешающий элемент. Полученные частные являются элементами ключевой строки следующей таблицы. В итоге получена вторая симплекс-таблица (табл. 1.4).

Таблица 1.4.

Вторая симплекс-таблица

Базис	Свободные члены	Свободные переменные
		x1	x2	x3	x4
y1	77 676	4,26	2,60	0	2,03
y2	18 919	0,14	0,50	1	0,54
y3	62 297	1,22	1,76	0	0,69
Индексная строка	4 200 000	15,60	-0,04	0	81,32

Так как в индексной строке появился отрицательный элемент, следует повторить все аналогичные этапы и построить третью симплекс-таблицу.

В итоге получена табл. 1.5.

Таблица 1.5.

Итоговая симплекс-таблица

Базис	Свободные члены	Свободные переменные
		x1	x2	x3	x4
y1	29 875	1,64	1	0	0,78
y2	3 981	-0,68	0	1	0,15
y3	9 716	-1,66	0	0	-0,68
Индексная строка	4 201 195	15,67	0	0	81,35

На основании таблицы 1.5 можно сделать выводы: в столбце свободных членов все элементы положительны (это значит, что полученное решение является допустимым); в индексной строке все элементы также положительны (это значит, что полученное решение – оптимально, т.е. максимизирует целевую функцию); оптимальным планом будут величины: (значит, они базисные);(так как они свободны); целевая функцияL=4 201 195.

Из таблицы 1.5 также следует, что базисная переменная y₃=9716, а свободные переменные y₁= y₂=0, т.е. в оптимальном плане резервы трудовых и материальных ресурсов равны нулю, так как они используются полностью. А резерв ресурсов оборудования y₂=9716, что свидетельствует о его излишках.

Таким образом, в результате применения метода линейного программирования принято решение о производстве джемперов мужских выбранной модели в количестве 3981 шт., свитеров мужских модели 55-1 в количестве 29 875 шт.
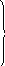
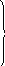