8.2.3. Алгоритмы разветвляющей структуры

Часто в зависимости от каких-либо промежуточных результатов вы­чис­ления производятся либо по одним, либо по другим формулам, т.е. в зависимости от выполнения некоторого логического условия вычислительный процесс осуществляется по одной или другой ветви.

Алгоритм такого вычислительного процесса называется алгорит­мом разветвляющей структуры.

1. Вычислить:

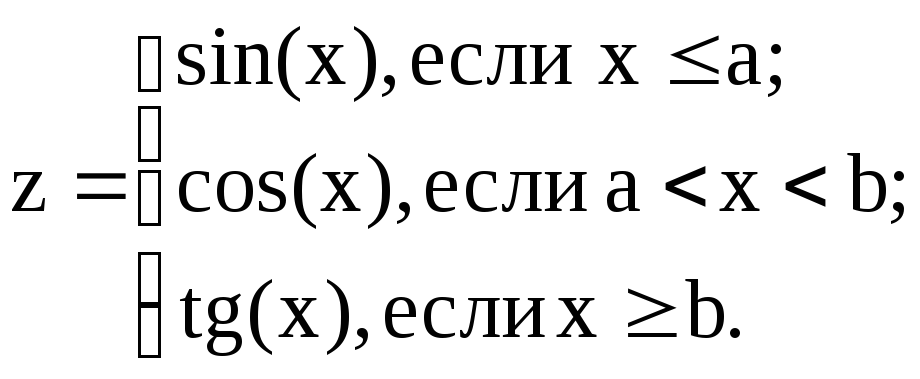
2. Найти квадрат наибольшего из двух чисел a и b и отпечатать

N = 1, если наибольшим является а, и признак N = 2 ‑ в противном случае.

3. Определить, попадает ли точка с координатами х, у в круг радиуса r (уравнение окружности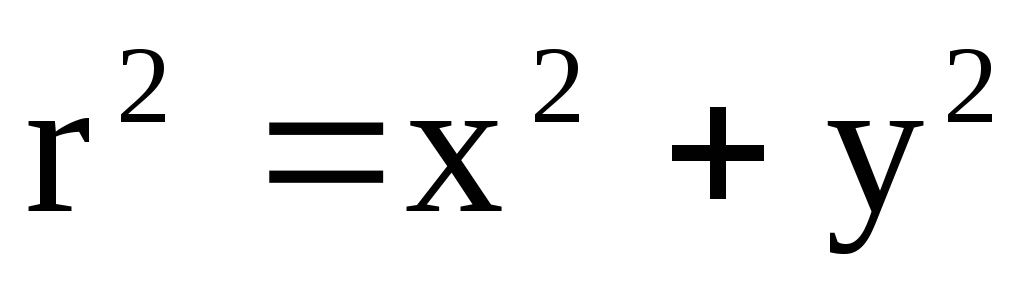). Вывести признак N = 1, если точка находится внутри круга, и признак N = 0, если точка находиться вне круга.

4. Составить программу, выполняющую упорядочение трех чисел A,B,C, таким образом, чтобы при выполнении ее в ячейке с симво­лическим адресомAнаходилось наименьшее число, в ячейкеB‑ сред­нее, в ячейкеC‑ наибольшее.

5. Записать указанное действие в виде одного условного оператора:

а) у =

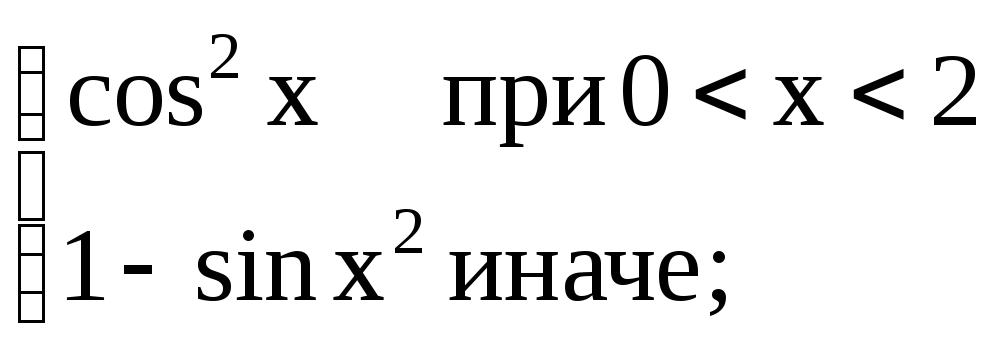
б) переменной х присвоить корень уравнения .

в) перераспределить значение переменных х и у так, чтобы в х оказалось большее из этих значений, а в у ‑ меньшее;

г) d = max (a, b, c);

д) z =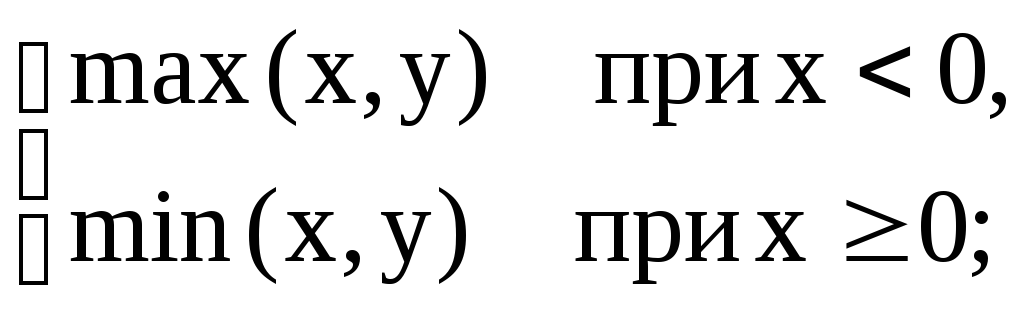

е) переменной k присвоить номер четверти плоскости, в которой находится точка с координатами х и у (ху0);

6. Записать программу для решения задачи:

а) по номеру у (у > 0) некоторого года определить с ‑ номер его столетия (учесть, что, к примеру, началом XX столетия был 1901);

б) ;

в) если уравнение ax²+ bx +c = 0 (a0) имеет вещественные корни, то логической переменной t присвоить значение True, а переменным xl и х2 ‑ сами корни, иначе переменной t присвоить False, а значение пере­мен­­ных xl и х2 не менять;

г) считая, что стандартные функции sin и cos применимы только к аргументам из отрезка [0, ], вычислить у = sin х для произвольного числа х;

д) значения переменных а, b и c поменять местами так, чтобы оказалось аbc.

8.2.3. Алгоритмы циклической структуры

Часто при решении задач приходится многократно вычислять значение по одним и тем же алгоритмам. Такие многократно повторяемые алгоритмы называются циклами. Различаютциклыс заданныминеизвестным числом повторений. К последним относятся итерационные циклы, характеризующиеся последовательным приближением к искомому значению с заданной точностью.

Для организации цикла необходимо выполнить следующие действия: 1) задать перед циклом начальное значение переменной, изменяющейся в цикле; 2) изменять переменную перед каждым новым повторением цикла; 3) проверять условие окончания или повторения цикла; 4) управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из него по окончании. Последние три функции выполняются многократно.

Переменная, изменяющаяся в цикле, называется параметром цикла.

1. Вычислить значения функции 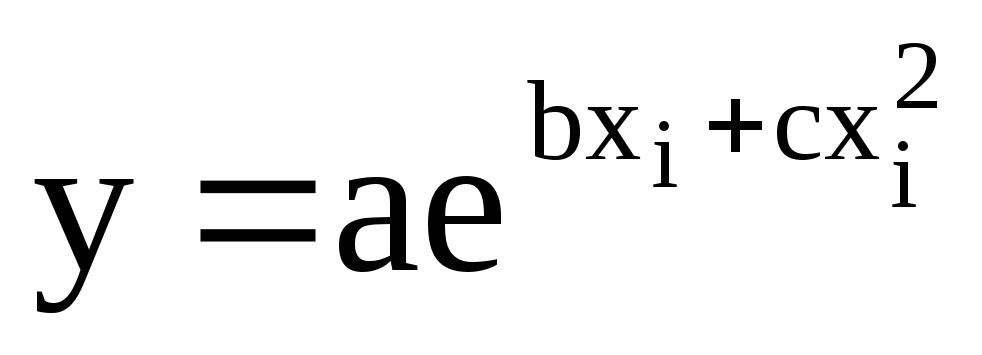, если Х задано массивом, состоящим из 40 элементов.

2. Вычислить и вывести на печать положительные значения функции у=sin (nx) ‑ cos (n/x) при n = 1, 2, …, 50.

3. Вычислить значения функции z = x^k/k, большие а, если k=1, 2, ….

4. Вычислить значения функции у = а³/(а²+ х²) при х, изменяющемся от 0 до 3 с шагом 0,1.

5. Напечатать таблицу значений аргумента х и функции

у(х) = а³/(а²+ х²) при значении х, изменяющихся от 0 до 3 с шагом 0,1.

6. Составить программу для вычисления значения функции у = 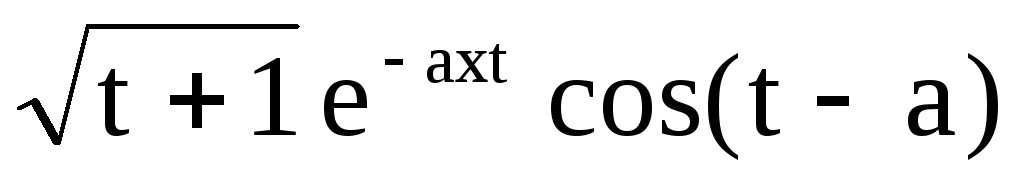при одновременном изменении аргументов t от 2 до 3 с шагом 0,2 и х от 1 до 2 для а = ‑2,1.

7. Составить программу вычисления n! (1 ^. 2^. 3^. 4^....^. n):

8. Составить программу, вычисляющую экстремальное значение функции 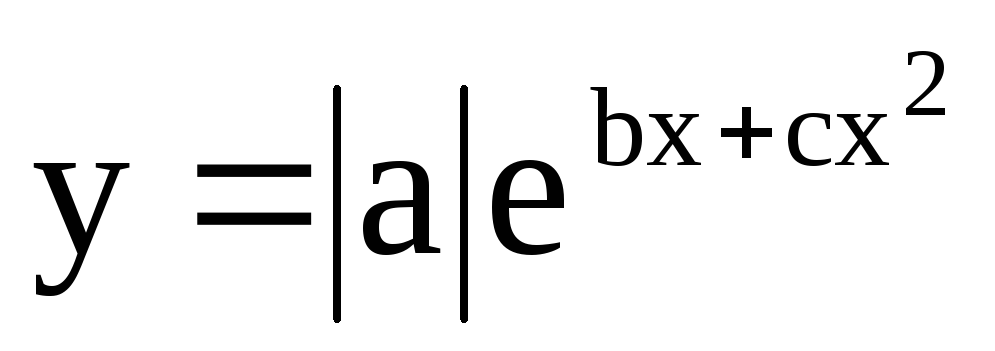при изменении аргумента х от 0 до 4 с шагом h.

9. Вычислить:

а) у = (2n ‑1)! = …, n >0;

б) у = (2n)! = …, n >0;

в) у = n!, n > 0.

10. Вычислить: у = .

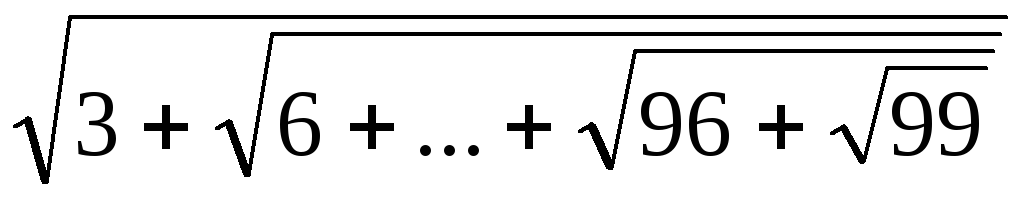11. Определить, является ли заданное натуральное число со­вер­шен­ным, т.е. равным сумме всех своих делителей, кроме самого этого числа (на­­пример, число 6 совершенно: 6=1+2+3).

12. Дано целое n >2. Напечатать простые числа из диапазона [2, n].

13. Найти сумму цифр заданного натурального числа.

14. Вычислить k ‑ количество точек с целочисленными коорди­на­та­ми, попадающих в круг радиуса R (R>0) с центром в начале координат.

15. Напечатать в возрастающем порядке все трехзначные числа, в де­­сятичной записи которых нет одинаковых цифр.

16. Даны целое n и вещественные числа 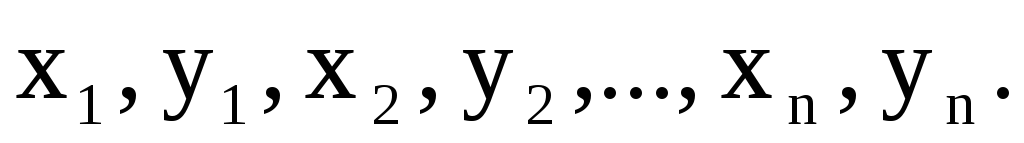Рассматривая пары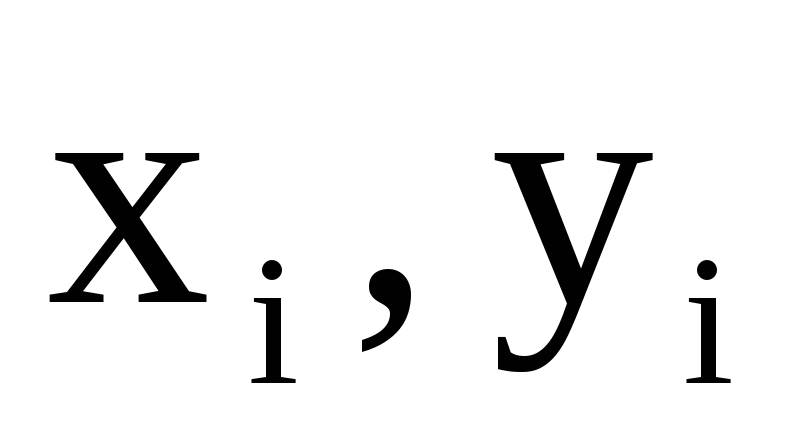как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки.

17. Напечатать все простые делители натурального числа.

18. Уравнение (предложена М.В. Дякиным).

Дана последовательность , ‑ натуральное число. Квадратные скобкиобозначают в формуле взятие целой части (округление до ближайшего меньшего целого числа). Обозначим .

Написать программу, которая для заданного натурального решает уравнение,

где - обозначение числа- факториал:.

Программа должна найти и сообщить:

1) точное значение xв виде несократимой дроби;

2) сумму цифр числителя и сумму цифр знаменателя этой дроби.

Образец вывода результата:

Число 6, числитель дроби X=10, знаменатель дробиX=63.

Сумма цифр числителя =1, сумма цифр знаменателя =9.

19. Задача «Кучи и яма» (предложена А.Б. Дернятиным).

Имеются яма и несколько куч (не более пяти) кирпичей. Разре­шает­ся перекладывать кирпичи из куч в яму по следующему правилу: если коли­чество кирпичей в куче больше, чем в яме, то можно переложить столько кирпичей, сколько находится в яме в данный момент. Требуется разработать алгоритм, который позволяет уложить в яму как можно боль­ше кирпичей.

Образец вывода результатов:

К1=150001 К2=81234 Я=70000 было

К1=150001 К2=11234 Я=140000 в яму из кучи 2‑й

К1=10001 К2=11234 Я=280000 в яму из кучи 1‑й

20. Представления натурального числа (предложена Д.Я.Шараевым).

Известно, что любое натуральное число N(0<N1000) может быть пред­­ста­вле­но в виде суммы квадратов не более четырех поло­жи­тель­ных целых чисел. Составьте программу, которая в ответ на ввод числаNвы­водит ко­ли­чествоSвсех различных представлений этого числа. Пред­­став­ления, отличающиеся лишь порядком слагаемых, считаются одинаковыми.

Пример.N=4.S=2. (1²+1²+1²+1²=4, 2²=4)

21. Задача «Многоугольник» (предложена Н.Ю. Лукояновым).

На плоскости декартовыми координатами своих вершин дан вы­пук­лый -угольник. Его вершины пронумерованы от 1 доnв порядке следо­ва­ния против часовой стрелки. Задан номер. Требуется провести че­рез-вершину-угольника два луча (назовем ихaиb) так, чтобы эти лучи делили-угольник на три равновеликие по площади части.

Входные данные: - число вершин; (х₁,y₁), (x₂,y₂), … , (x_n,y_n) - координаты 1-й, 2-й, и т.д.-й вершины соответственно;- номер выделенной вершины.

Выходные величины: координаты (х_а,y_a) и (x_b,y_b) точек пересечения лучейaиbс границей-угольника.