14 Відстань від точки до прямої на площині і від точки до прямої в просторі. Відстань між мимобіжними прямими

15. Кут між площинами. Кут між прямими на площині. У мова паралельності і перпендикулярності площин і прямих на площині

Пусть заданы две плоскости Q₁ и Q₂:Под углом между плоскостями Q₁ и Q₂ понимается один из двугран­ных углов, образованных этими плоскостями.Угол    между  нормальными  векторами  иплоскостей Q₁ и Q₂ равен одному из этих углов (см. рис. 72).Если плоскости Q₁ и Q₂ перпендикулярны    (см. рис. 73, а), то таковы же их нормали, т. е. n1_|_n2 (и наоборот). Но тогда n1*n2=0, т. е. . (A1A2)Полученное равенство есть условие перпендикулярности двух плоскостей Q₁ и Q₂.Если плоскости Q₁ и Q₂ параллельны (см. рис. 73, б), то будут параллельны и их нормали n1 и n2 (и наоборот). Но тогда, как известно координаты векторов пропорциональны: . Это и есть уcловиє параллельности двух плоскостей Q₁ и Q₂. Угол между прямыми. Условия параллельности и перпендикулярности прямых

Пусть прямые L₁ и L₂ заданы уравнениями   Под углом между этими прямыми понимают угол между направляющими векторамии(см. рис. 78). Поэтому, по известной формуле для косинуса угла между векторами, получаемили(12.16)Для нахождения острого угла между прямыми L₁ и L₂ числитель правой части формулы (12.16) следует взять по модулю.

Если прямые L₁ и L₂ перпендикулярны, то в этом и только в этом случае имеем cos Следоват ельно, числитель дроби (12.16) равен нулю, т. е. Если прямые L₁ и L₂ параллельны, то параллельны их направляющие векторы s1 и s2. Следовательно, координаты этих векторов пропорциональны, т. е. .

16.Кут між прямими у просторі. Кут між прямою і площиною,умова паралельності і перпендикулярності прямих в просторі,прямої і площини. Предыдущийй вопрос

Пусть плоскость Q задана уравнением , а прямая L уравнениями. Углом между прямой и плоскостью называет­ся любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Обозначим через φ угол между плоскостью Q и прямой L, а через  — угол между векторамии(см. рис. 80). Тогда. При этом: если, то; если, то.(12.17)Острый угол между плоскостью Q и прямой L можно найти, взяв в фор­муле (12.17) модуль правой части.Если прямая L параллельна плоскости Q, то векторыn и s перпенди­кулярны (см. рис. 81), а потому s*n=0, т. е.является условием параллельности прямой и плоскости.Если прямая L перпендикулярна плоскости Q, то векторыn и s параллельны       (см. рис. 82). Поэтому равенства   являются условиями перпендикулярности прямой и плоскости.Пересечение прямой с плоскостью. Условие принадлежности прямой плоскостиПусть требуется найти точку пересечения прямой(12.18)с плоскостью(12.19)Для этого надо решить систему уравнений (12.18) и (12.19). Проще всего это сделать, записав уравнения прямой (12.18) в параметрическом виде:Подставляя эти выражения для х, у и z в уравнение плоскости (12.19), получаем уравнениеили.   (12.20)Если прямая L не параллельна плоскости, т. е. если,то из равенства (12.20) находим значение t:Подставляя найденное значение t в параметрические уравнения прямой найдем координаты точки пересечения прямой с плоскостью. Рассмотрим теперь случай, когда:а)  если, то прямая L параллельна плоскости и пересекать ее не будет (уравнение (12.20) решения не имеет так как имеет вид , где 0*t+F=0 F!=0);

б)  если , то уравнение (12.20) имеет видt*0+0=0; ему удовлетворяет любое значение t, любая точка прямой является точкой пересечения прямой и плоскости. Заключаем: прямая лежит в плоскости. Таким образом, одновременное выполнение равенствявляется условием принадлежности прямой плоскости.

17.Криві другого порядку. Коло. Еліпс. Ексцентриситет,директриси еліпса,їх властивості.Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат(11.1)Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Окружность Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R с центром в точке M0 называется множе­ство всех точек Μ плоскости, удовлетворяющих условию m. Пусть точка M0M в прямоугольной системе координат  имеет координаты x₀, y₀ а M(x,y) — произвольная точка окружности (см. рис. 48).Тогда из условия M0M=R получаем уравнение, то есть(11.2)Уравнению (11.2) удовлетворяют координаты любой точкиM(x,y) данной окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности.Уравнение (11.2) называется каноническим уравнением окружностиВ частности, полагая x0=0 и y0=0, получим уравнение окружности с центром в начале координат .Уравнение окружности (11.2) после несложных преобразований примет вид. При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:1)  коэффициенты при x² и у² равны между собой;2) отсутствует член, содержащий произведение xу текущих координат. Рассмотрим обратную задачу. Положив в уравнении (11.1) значения B=0 и A=C!=0, получим(11.3)Преобразуем это уравнение:(дельтаэтоA)т.е.      ,т.е.(11.4)Отсюда следует, что уравнение (11.3) определяет окружность при условии . Ее центр находится в точке, а радиус.Если же, то уравнение (11.3) имеет вид.Ему удовлетворяют координаты  единственной точки. В этом случае говорят : “окружность выродилась в точку” (имеет нулевой радиус).Если, то уравнение (11.4), а следовательно, и равносильное уравнение (11.3), не определят никакой линии, так как правая часть уравнения (11.4) отрицательна, а левая – не отрицательная (говорять: “окружность мнимая” ).Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.Обозначим фокусы через F₁ и F₂, расстояние между ними через 2c, а сумму расстояний от произ­вольной точки эллипса до фокусов — через 2a (см. рис. 49). По определению 2a > 2c, т. е. a > c.Для вывода уравнения эллипса выберем систему координат  так, чтобы фокусы F₁ и F₂  лежали на оси 0x, а начало координат совпадало с серединой отрезка F₁F₂. Тогда фокусы будут иметь следующие координаты: F1(-c;0) и F2(c;0).Пусть M(x,y) — произвольная точка эллипса. Тогда, согласно определению эллипса,  MF1+MF2=2a, т. е.(11.5)Это, по сути, и есть уравнение эллипса.Преобразуем уравнение  (11.5)  к более простому виду следующим образом:,,.Так какa>с, то a^2-c^2>0. Положим     (11.6) Тогда последнее уравнение примет видили(11.7)Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называетсяканоническимуравнением эллипса.Эллипс — кривая второго порядка.Исследование формы эллипса по его уравнениюУстановим форму эллипса, пользуясь его каноническим уравнением.1. Уравнение (11.7) содержит х и у только в четных степенях, поэтому если точка (x;y) принадлежит эллипсу, то ему также принадлежат точки (x;-y),(-x;y),(-x;-y). Отсюда следует, что эллипс симметричен относительно осей ox и oy, а также относительно точки o(0;0), которую называют центром эллипса.2.  Найдем точки пересечения эллипса с осями координат. Положив y=0, находим две точки и, в которых осьox пересекает эллипс (см. рис. 50). Положив в уравнении (11.7) x=0, находим точки пересечения эллипса с осью ox: и. ТочкиA₁, A₂ , B₁, B₂ называются вершинами эллипса . Отрезки A₁A₂ и B₁B₂, а также их длины 2a и 2b называются соответственно большой и малой осями эллипса. Числа a и b называются соответственно боль­шой и малой полуосями эллипса.3.  Из  уравнения   (11.7)   следует, что каждое слагаемое в левой части не превосходит единицы, т.е. имеют место неравенства  иилии. Следовательно, все точки эллипса .лежаї внутри прямоугольника, образованного прямыми.4. В уравнении (11.7) сумма неотрицательных слагаемыхиравна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если |x| возрастает, то |y| уменьшается и наоборот. Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).Дополнительные сведения об эллипсеФорма эллипса зависит от отношения  b/a. При b=a эллипс превращается в окружность, уравнение эллипса (11.7) принимает вид . В качестве характеристики формы эллипса чаще пользуются отношениемc/a.   Отношение c/a  половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и o6oзначается буквой ε («эпсилон»): (11.8)причем  0<ε< 1, так как 0<с<а. С учетом равенства  (11.6) формулу  (11.8)  можно переписать в видеОтсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить ε = 0, то эллипс превращается в окружность.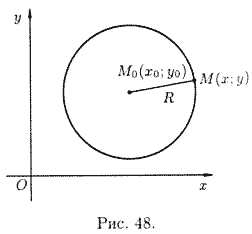

Пусть М(х;у) -- произвольная точка эллипса с фокусами F₁ и F₂ (см. рис. 51). Длины отрезков F₁M=r₁ и F₂M = r₂ называются фокальными радиусами точ­ки Μ. Очевидно, r1+r2=2aИмеют место формулы r1=a+ex и r2=a-ex Прямые x=+-a/e называются директрисамы элипса.Теорема 11.1. Если  r— расстояние от произвольной точки эллипса до какого-нибудь фокуса, d — расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету  эллипса: r/d=e.Из равенства (11.6) следует, что a>b. Если же a<b, то уравнение (11.7) определяет эллипс, большая ось которого 2b лежит на оси Оу, а малая ось 2a — на оси  Ох (см. рис. 52). Фокусы такого эллипса находятся в точках F1(0;c) и F2(0;-c), где .

18.Гіпербола.Асимптоти гіперболи. Ексцентриситет. директриси гіперболи,їх властивості.Каноническое уравнение гиперболыГиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.Обозначим фокусы через F₁ и F₂ расстояние между ними через 2с, а модуль разности расстоя­ний от каждой точки гиперболы до фокусов через 2a. По определению 2a < 2с, т. е. a < c.Для вывода уравнения гиперболы выберем си­стему координат oxy так, чтобы фокусы F₁ и F₂  лежали на оси oy, а начало координат совпало с серединой отрезка F₁F₂ (см. рис. 53). Тогда фокусы будут иметь координаты F1 и F2Пусть M — произвольная точка гиперболы. Тогда согласно опре­делению гиперболы или, т.е.. После упрощений, как это было сделано при выводе уравнения эллипса, получимканоническое уравнение гиперболы                         (11.9)(11.10)Гипербола есть линия второго порядка.Дополнительные сведения о гиперболе Эксцентриситетом гиперболы (11.9) называется отношение расстояния между фокусами к величине действительной оси гиперболы, обозначается ε: Так как для гиперболыc>a, то эксцентриситет гиперболы больше единицы: e>1. Эксцентриситет характеризует форму гиперболы. Дей­ствительно, из равенства (11.10) следует, что т.е.и.Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение — ее полуосей, а значит, тем более вытянут ее основной прямоугольник.Эксцентриситет равносторонней гиперболы равен корень из 2. Действительно,Прямыеx=+-a/e —  называются директрисами гиперболы. Так как для гиперболы ε > 1, то a/e<a. Это значит, что правая директриса расположена между центром и правой вершиной гиперболы, левая — между центром и левой вершиной.Директрисы гиперболы имеют то же свойство r/d=e, что и директрисы  эллипса.Кривая, определяемая уравнением также есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2a — на оси Ох. На рисунке 59 она изображена пунктиром.

  

Очевидно, что гиперболы  иимеют общие асимптоты. Такие гиперболы называются сопряженными.

19.Парабола.Директриси параболи. Їх властивості. Загальне означення кривої другого порядку(17)

Каноническое уравнение параболы

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0).Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директри­сой (см. рис. 60). В выбранной системе фокус F имеет координаты , а уравнение директрисы имеет вид, или.ПустьM(x;y) — произвольная точка параболы. Соединим точку Μ с F. Проведем отрезок ΜΝ пер­пендикулярно директрисе. Согласно определению параболы MF = ΜΝ. По формуле расстояния между двумя точками на­ходим:Следовательно,Возведя обе части уравнения в квадрат, получимт. е.(11.13)Уравнение (11.13) называется каноническим уравнением параболы. Парабола есть линия второго порядка.