
- •Т е о р і я й м о в і р н о с т е й т а
- •03056, Київ-56, просп. Перемоги, 37 Зміст
- •1. Елементи комбінаторики
- •2. Біноміальні тотожності
- •3. Формула включень та виключень
- •4. Класичне означення ймовірності
- •5. Геометричний метод знаходження ймовірності
- •6. Умовні ймовірності, незалежні події, формула повної ймовірності, формула Байєса
- •Дискретні випадкові величини, математичне сподівання та дисперсія
- •Загальне поняття випадкової величини, функції від випадкових величин
- •Граничні теореми
- •0.74 1.12 3.75 4.33 5.71 6.09 7.89 8.03 9.55 10.22.
- •Список використаної літератури
Граничні теореми
Нерівність Чебишева. Якщо випадкова величина
 має скінченну дисперсію, то для
будь-якого
має скінченну дисперсію, то для
будь-якого має місце нерівність
має місце нерівність
![]() (38)
(38)
Узагальнення.
Нехай
![]() – це борелівська функція, визначена на
– це борелівська функція, визначена на![]() ,
причому
,
причому![]() для будь-якого
для будь-якого![]() та
та![]() – монотонно неспадна функція на
– монотонно неспадна функція на![]() .
Якщо
.
Якщо
![]() ,
то для
будь-якого
,
то для
будь-якого
![]() має місце нерівність
має місце нерівність
![]()
Приклад 1. По мішені було зроблено 1000 пострілів. Ймовірність влучення при кожному пострілі дорівнює 0.7. Оцінити за допомогою нерівності Чебишева ймовірність того, що кількість влучень знаходиться в межах від 670 до 730 включно.
Розв’язання.
Позначимо
через
![]() кількість влучень. Очевидно, що
кількість влучень. Очевидно, що![]() має розподіл Бернуллі з кількістю
випробувань
має розподіл Бернуллі з кількістю
випробувань![]() та ймовірністю успіху
та ймовірністю успіху![]() .
У цьому випадку
.
У цьому випадку
![]()
![]() .
Скориставшись формулою (38), маємо
.
Скориставшись формулою (38), маємо
![]()
![]()
тобто з імовірністю не меншою, ніж 0.767, можна стверджувати, що кількість влучень буде знаходитись у вказаних межах.
Приклад
2.
Випадкова величина
![]() має щільність розподілу
має щільність розподілу
![]()
Довести нерівність
![]()
Доведення.
Скористаємось нерівністю Чебишева
(38). Випадкова величина
![]() має щільність розподілу Ерланга з
параметром
має щільність розподілу Ерланга з
параметром![]() ,
тобто
,
тобто![]() ,
де
,
де![]() – незалежні експоненціально розподілені
випадкові величини з параметром
– незалежні експоненціально розподілені
випадкові величини з параметром![]() .
В цьому випадку
.
В цьому випадку![]() ,
тобто
,
тобто![]() .
Таким чином,
.
Таким чином,
![]()
![]()
що і треба було довести.
Послідовність випадкових величин
 збігається до випадкової величини
збігається до випадкової величини за
ймовірністю,
якщо для будь-якого
за
ймовірністю,
якщо для будь-якого

![]()
Теорема
Чебишева про закон великих чисел.
Нехай
![]() – це послідовність попарно незалежних
випадкових величин із скінченними
дисперсіями, які є рівномірно обмеженими,
тобто
– це послідовність попарно незалежних
випадкових величин із скінченними
дисперсіями, які є рівномірно обмеженими,
тобто![]() для деякого
для деякого![]() .
Тоді для будь-якого
.
Тоді для будь-якого![]() має місце співвідношення
має місце співвідношення
 (39)
(39)
Теорема
Маркова.
Нехай
![]() – це послідовність випадкових величин
(можливо залежних) така, що
– це послідовність випадкових величин
(можливо залежних) така, що
 (40)
(40)
Тоді має місце закон великих чисел (39).
Теорема
Бернуллі.
Нехай
![]() – це кількість появи події
– це кількість появи події![]() у
у![]() незалежних випробуваннях, а
незалежних випробуваннях, а![]() – це ймовірність появи події
– це ймовірність появи події![]() у кожному випробуванні. Тоді для
будь-якого
у кожному випробуванні. Тоді для
будь-якого![]() має місце співвідношення
має місце співвідношення
![]()
Теорема
Пуассона.
Нехай
![]() – це кількість появи події
– це кількість появи події![]() у
у![]() незалежних випробуваннях, а
незалежних випробуваннях, а![]() – це ймовірність появи події
– це ймовірність появи події![]() у
у![]() -му
випробуванні. Тоді для будь-якого
-му
випробуванні. Тоді для будь-якого![]() має місце співвідношення
має місце співвідношення
![]()
Приклад
3.
Нехай
![]() – це послідовність незалежних випадкових
величин така, що
– це послідовність незалежних випадкових
величин така, що![]() приймає значення
приймає значення![]() відповідно з ймовірностями
відповідно з ймовірностями![]() де
де![]() .
Чи може бути застосована теорема Чебишева
до цієї послідовності?
.
Чи може бути застосована теорема Чебишева
до цієї послідовності?
Розв’язання.
Згідно з теоремою Чебишева достатньо
перевірити, чи виконана умова рівномірної
обмеженості дисперсій
![]() .
Очевидно, що
.
Очевидно, що![]() .
Тому
.
Тому
![]() .
.
Функція
![]() досягає свого максимуму при
досягає свого максимуму при![]() .
Оскільки
.
Оскільки![]() – ціле число, то треба порівняти значення
– ціле число, то треба порівняти значення![]() при
при![]() та
та![]() – найближчих цілих до
– найближчих цілих до![]() Маємо:
Маємо:![]() Тому
Тому
![]() ,
і теорема Чебишева може бути застосована
до послідовності випадкових величин
із вказаними властивостями.
,
і теорема Чебишева може бути застосована
до послідовності випадкових величин
із вказаними властивостями.
Приклад
4.
Нехай
![]() – це послідовність незалежних випадкових
величин така, що
– це послідовність незалежних випадкових
величин така, що![]() приймає значення
приймає значення![]() і
і![]() з однаковою ймовірністю 0.5. Довести, що
середнє арифметичне послідовності
незалежних випадкових величин
з однаковою ймовірністю 0.5. Довести, що
середнє арифметичне послідовності
незалежних випадкових величин![]() задовольняє закон великих чисел (39).
задовольняє закон великих чисел (39).
Доведення.
Скористаємось
теоремою Маркова. Очевидно, що
![]() .
Тому
.
Тому
![]() .
Враховуючи незалежність випадкових
величин
.
Враховуючи незалежність випадкових
величин
![]() ,
співвідношення (40) матиме вигляд
,
співвідношення (40) матиме вигляд
 ,
,
тобто виконана достатня умова теореми Маркова і має місце співвідношення (39).
Теорема Хінчина. Нехай
 – послідовність незалежних і однаково
розподілених випадкових величин із
скінченним математичним сподіванням
– послідовність незалежних і однаково
розподілених випадкових величин із
скінченним математичним сподіванням .
Тоді для будь-якого
.
Тоді для будь-якого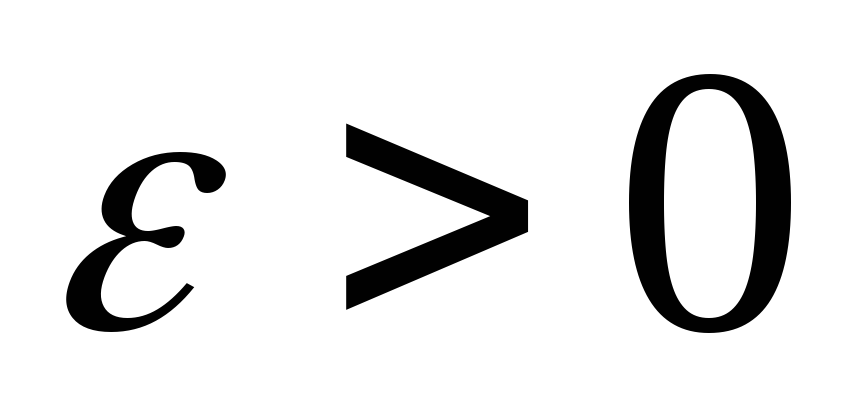 має місце співвідношення
має місце співвідношення

Теорема
(необхідна
та достатня умова виконання закону
великих чисел).
Для
того, щоб послідовність
![]() (як завгодно залежних) випадковихвеличин
задовольняла закону великих чисел (39)
необхідно і достатньо, щоб було виконано
співвідношення
(як завгодно залежних) випадковихвеличин
задовольняла закону великих чисел (39)
необхідно і достатньо, щоб було виконано
співвідношення

Нехай
![]() – це імовірнісний простір.Послідовність
випадкових величин
– це імовірнісний простір.Послідовність
випадкових величин
![]() збігається до випадкової величини
збігається до випадкової величини![]() з
ймовірністю 1 (або
майже
напевно),
якщо для будь-якого
з
ймовірністю 1 (або
майже
напевно),
якщо для будь-якого
![]() ,
де
,
де![]() і
і![]() ,
виконується співвідношення
,
виконується співвідношення
![]()
Із збіжності з ймовірністю 1 випливає збіжність за ймовірністю.
Теорема
Колмогорова
(посилений
закон великих чисел).
Якщо послідовність взаємно незалежних
випадкових величин
![]() задовольняє умову
задовольняє умову
![]() ,
,
то виконується посилений закон великих чисел:
![]() з
ймовірністю 1.
з
ймовірністю 1.
Теорема
(також
належить А.М.Колмогорову). Для послідовності
незалежних однаково розподілених
випадкових величин
![]() виконується посилений закон великих
чисел
виконується посилений закон великих
чисел
![]() з
ймовірністю 1
з
ймовірністю 1
тоді
і лише тоді, коли існує скінчене
математичне сподівання
![]()
Приклад
5.
Чи можна застосувати теорему Хінчина
до послідовності
![]() незалежних випадкових величин, що мають
одну й ту ж саму функцію розподілу
незалежних випадкових величин, що мають
одну й ту ж саму функцію розподілу![]() ?
?
Розв’язання.
Достатньою умовою застосування теореми
Хінчина є скінченність
![]() Перевіримо цю умову. Маємо
Перевіримо цю умову. Маємо
![]()
тобто математичне сподівання не існує і теорему Хінчина не можна застосовувати.
Приклад
6.
Чи можливо наближено обчислити інтеграл
![]() методом Монте-Карло за формулою
методом Монте-Карло за формулою
![]() ,
,
де
![]() – це послідовність незалежних рівномірно
розподілених у
– це послідовність незалежних рівномірно
розподілених у![]() випадкових величин.
випадкових величин.
Розв’язання.
Величина
![]() вважається наближеним значенням
вважається наближеним значенням![]() ,
якщодля
будь-якого
,
якщодля
будь-якого
![]() має місце співвідношення
має місце співвідношення
![]()
тобто
має місце закон великих чисел. Оскільки
випадкові величини
![]() мають однаковий розподіл, то і функції
мають однаковий розподіл, то і функції![]() від них також мають однаковий розподіл.
Перевіримо, чи виконана умова теореми
Хінчина, яка полягає у тому, що
від них також мають однаковий розподіл.
Перевіримо, чи виконана умова теореми
Хінчина, яка полягає у тому, що
![]() ,
де
,
де
![]() – це випадкова величина, рівномірно
розподілена у
– це випадкова величина, рівномірно
розподілена у![]() .
Маємо
.
Маємо
![]()
Оскільки
![]() ,
,
то
![]() ,
тобто метод Монте-Карло не можна
застосовувати для наближеного обчислення
величини
,
тобто метод Монте-Карло не можна
застосовувати для наближеного обчислення
величини![]() .
.
Узагальнення схеми Бернуллі з незалежними випробуваннями. Нехай проводяться
 незалежних випробувань, в результаті
кожного з яких може відбутися одна з
незалежних випробувань, в результаті
кожного з яких може відбутися одна з подій
подій ,
що утворюють повну групу подій. Подія
,
що утворюють повну групу подій. Подія може відбутися з ймовірністю
може відбутися з ймовірністю ,
, .
Якщо
.
Якщо ,
то отримуємо схему Бернуллі. Позначимо
через
,
то отримуємо схему Бернуллі. Позначимо
через ймовірність того, що в
ймовірність того, що в іспитах події
іспитах події відбудуться відповідно
відбудуться відповідно разів,
разів, Очевидно, що
Очевидно, що
![]()
Позначимо
![]()
Локальна
гранична теорема.
Якщо
![]() то при
то при![]() має місце співвідношення
має місце співвідношення

рівномірно
для всіх
![]() ,
для яких
,
для яких![]() знаходяться в довільних скінчених
проміжках
знаходяться в довільних скінчених
проміжках![]() .
.
Розглянемо
випадок, коли
![]()
Локальна
гранична теорема Муавра-Лапласа.
Якщо ймовірність появи деякої події
![]() в
в![]() незалежних випробовуваннях не змінюється
і дорівнює
незалежних випробовуваннях не змінюється
і дорівнює![]() ,
,![]() ,
то ймовірність
,
то ймовірність![]() того, що в
того, що в![]() випробуваннях подія
випробуваннях подія![]() відбудеться
відбудеться![]() разів задовольняє співвідношення
разів задовольняє співвідношення
![]() (41)
(41)
рівномірно
для всіх
![]() ,
для яких
,
для яких![]() знаходяться в довільному скінченому
проміжку.
знаходяться в довільному скінченому
проміжку.
Приклад 7. Підприємство виробляє деякі деталі. Ймовірність того, що деталь виявиться бракованою дорівнює 0.005. Знайти ймовірність того, що серед 10 000 навмання взятих деталей виявиться 40 бракованих?
Розв’язання.
Застосуємо теорему Маувра-Лапласа. В
нашому випадку
![]() .
Згідно з (41) ймовірність
.
Згідно з (41) ймовірність
![]() оцінюється за наближеною формулою
оцінюється за наближеною формулою
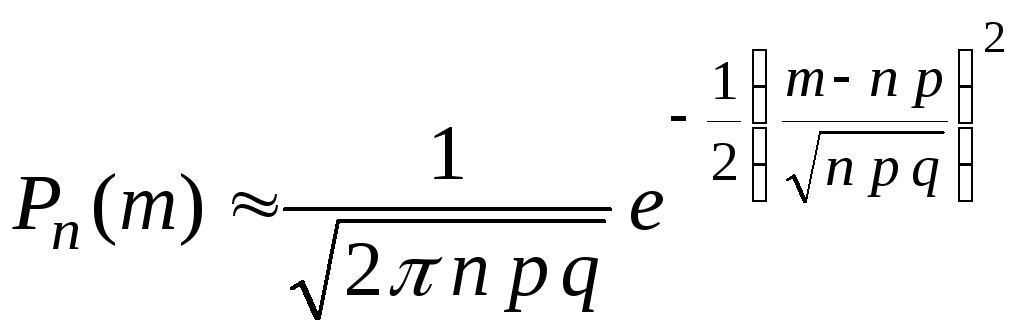 .
.
Оскільки
![]() ,
то
,
то
![]() .
.
Гранична теорема для послідовності незалежних однаково розподілених випадкових величин. Якщо
 – це незалежні однаково розподілені
випадкові величини з математичним
сподіванням
– це незалежні однаково розподілені
випадкові величини з математичним
сподіванням та скінченною дисперсією
та скінченною дисперсією ,
то при
,
то при рівномірно відносно
рівномірно відносно

де
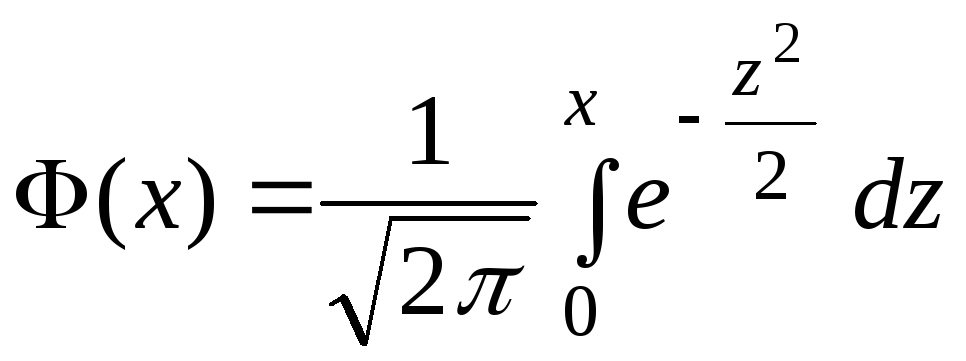 (42)
(42)
– це функція Лапласа, значення якої задаються відповідною таблицею.
Інтегральна
гранична теорема Муавра-Лапласа.
Нехай
проводиться серія незалежних випробувань,
результатом кожного з яких є “успіх”
з
ймовірністю
![]() ,
,![]() ,
і “невдача” з ймовірністю
,
і “невдача” з ймовірністю![]() .
Якщо
.
Якщо![]() – це кількість “успіхів”
у
– це кількість “успіхів”
у
![]() випробуваннях, то рівномірно відносно
випробуваннях, то рівномірно відносно![]() і
і![]()
![]() при
при
![]() має
місце співвідношення
має
місце співвідношення
![]()
Нехай
![]() – це послідовність взаємно незалежних
випадкових величин, які мають скінченні
математичні сподівання та дисперсії.
Позначимо:
– це послідовність взаємно незалежних
випадкових величин, які мають скінченні
математичні сподівання та дисперсії.
Позначимо:
![]()
Умова
Ліндеберга. Для
будь-якого
![]()
![]() (43)
(43)
де
![]() – це функція розподілу випадкової
величини
– це функція розподілу випадкової
величини![]() .
.
Центральна
гранична теорема. Якщо
послідовність взаємно незалежних
випадкових величин задовольняє умову
Ліндеберга (43), то при
![]() рівномірно
відносно
рівномірно
відносно
![]() має місце співвідношення
має місце співвідношення
 (44)
(44)
Теорема
Ляпунова. Достатньою
умовою виконання співвідношення (44) є
існування деякого
![]() такого, що
такого, що
![]()
Приклад
8.
Ймовірність виходу з ладу деякого
приладу під час його випробувань на
надійність дорівнює
![]() .
Чому дорівнює ймовірність того, що під
час випробувань 1 000 приладів вийдуть
з ладу:a)
не
менше 10 приладів; b)
не більше 10 приладів; c)
від 7 до 12 приладів?
.
Чому дорівнює ймовірність того, що під
час випробувань 1 000 приладів вийдуть
з ладу:a)
не
менше 10 приладів; b)
не більше 10 приладів; c)
від 7 до 12 приладів?
Розв’язання.
Для
наближеного обчислення ймовірностей
вказаних подій скористаємось інтегральною
граничною теоремою Муавра-Лапласа. У
нашому випадку
![]() .
Оскільки значення
.
Оскільки значення![]() є скінченним, то наближена формула має
такий вигляд:
є скінченним, то наближена формула має
такий вигляд:
![]()
![]()
![]()
де
![]() – це кількість відмов. Тому
– це кількість відмов. Тому
![]()
![]()
![]()
![]()
![]()
Приклад
9.
Скільки потрібно провести незалежних
випробувань для того, щоб з ймовірністю
0.9 подія
![]() відбулась не менше 10 разів, якщо відомо,
що ймовірність її появи у одному
випробуванні дорівнює 0.05?
відбулась не менше 10 разів, якщо відомо,
що ймовірність її появи у одному
випробуванні дорівнює 0.05?
Розв’язання.
Якщо позначити через
![]() кількість появ події
кількість появ події![]() у
у![]() випробуваннях, то згідно з теоремою
Муавра-Лапласа (див. також попередній
приклад) маємо
випробуваннях, то згідно з теоремою
Муавра-Лапласа (див. також попередній
приклад) маємо
![]()

![]()
Враховуючи
те, що
![]() маємо
маємо
![]()
вже
при
![]() .
Тому
.
Тому
![]()
З таблиці для функції Лапласа знаходимо, що
![]()
Функція
![]() монотонно зростає за
монотонно зростає за![]() .
Найменше ціле число, при якому
.
Найменше ціле число, при якому![]() дорівнює 161, тобто
дорівнює 161, тобто![]() випробування буде досить для того, щоб
з ймовірністю 0.9 подія
випробування буде досить для того, щоб
з ймовірністю 0.9 подія![]() відбулась не менше 10 разів.
відбулась не менше 10 разів.
Приклад 10. Скільки потрібно провести незалежних випробувань для обчислення інтеграла
![]()
методом Монте-Карло для того, щоб з ймовірністю 0.95 відносна похибка не перевищувала 2%?
Розв’язання.
Зробивши заміну змінної
![]() ,
інтеграл
,
інтеграл![]() можна подати у такому вигляді:
можна подати у такому вигляді:
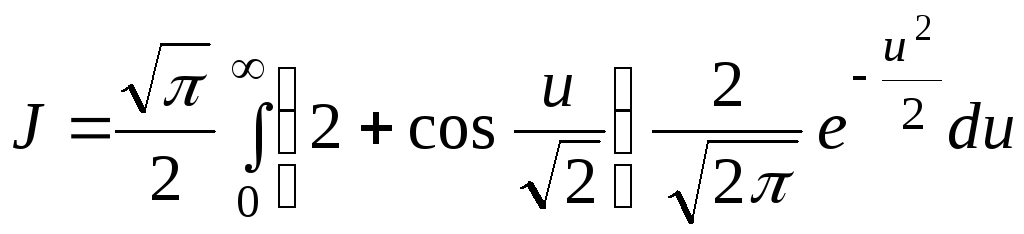 .
.
Зауважимо,
що
![]() є щільністю розподілу випадкової
величини
є щільністю розподілу випадкової
величини
![]() ,
де
,
де![]() – нормально розподілена випадкова
величина з параметрами 0 та 1. Тому
інтеграл
– нормально розподілена випадкова
величина з параметрами 0 та 1. Тому
інтеграл
![]() можна розглядати, як математичне
сподівання:
можна розглядати, як математичне
сподівання:
![]() .
.
Згідно загальної схеми метода Монте-Карло наближене значення інтегралу обчислюється за формулою
![]() ,
,
![]() ,
,
де
![]() – це незалежні нормально розподілені
випадкові величини з параметрами 0 та
1, а
– це незалежні нормально розподілені
випадкові величини з параметрами 0 та
1, а![]() – це загальна кількість проведених
випробувань.
– це загальна кількість проведених
випробувань.
Скористаємось граничною теоремою для послідовності незалежних однаково розподілених випадкових величин. Позначимо
![]()
Згідно цієї теореми
 (45)
(45)
Відносна
похибка
визначається виразом
![]() .
Оскільки
.
Оскільки
![]() ,
то співвідношення
(45) можна переписати у такому вигляді:
,
то співвідношення
(45) можна переписати у такому вигляді:
![]()
Прирівнюючи
праву частину до заданої ймовірності
![]() і розв’язуючи рівняння
і розв’язуючи рівняння
![]() ,
знаходимо
,
знаходимо
![]() .
Для того, щоб відносна похибка
.
Для того, щоб відносна похибка![]() була меншою, ніж 2%, потрібно, щоб
була меншою, ніж 2%, потрібно, щоб
![]() ,
тобто
,
тобто
![]()
Оскільки
точні значення
![]() та
та![]() нам невідомі, то можна скористуватись
елементарними оцінками
нам невідомі, то можна скористуватись
елементарними оцінками
![]() .
.
Таким чином, робимо остаточний висновок, що кількість випробувань
![]()
буде
цілком достатньою для оцінки інтеграла
![]() методом Монте-Карло з відносною похибкою,
меншою, ніж 2%. Оскільки для
методом Монте-Карло з відносною похибкою,
меншою, ніж 2%. Оскільки для![]() та
та![]() були використані відповідно оцінки
знизу та зверху, то
були використані відповідно оцінки
знизу та зверху, то![]() є завищеною оцінкою кількості випробувань
(для отримання оцінки з вказаною точністю
насправді потрібно зробити у декілька
разів меншу кількість випробувань).
Тому на практиці замість аналітичних
оцінок використовують незміщені оцінки
є завищеною оцінкою кількості випробувань
(для отримання оцінки з вказаною точністю
насправді потрібно зробити у декілька
разів меншу кількість випробувань).
Тому на практиці замість аналітичних
оцінок використовують незміщені оцінки![]() та
та![]() .
.
Елементи математичної статистики
Емпірична функція розподілу. Набір значень
 випадкової величини
випадкової величини ,
який отримано в результаті експерименту,
називаєтьсявибіркою
з
генеральної сукупності.
Значення вибірки, впорядковані у
зростаючому порядку, називаються
варіаційним
рядом:
,
який отримано в результаті експерименту,
називаєтьсявибіркою
з
генеральної сукупності.
Значення вибірки, впорядковані у
зростаючому порядку, називаються
варіаційним
рядом:
 .Емпіричною
функцією розподілу називається
функція
.Емпіричною
функцією розподілу називається
функція
 :
:

Приклад 1. Знайти емпіричну функцію розподілу вибірки
![]() 4 1 7 12 5
4 1 7 12 5
![]() 5 2 4 6 3
5 2 4 6 3
(значення
![]() у вибірці зустрічається
у вибірці зустрічається![]() разів).
разів).
Розв’язання. Перш за все треба побудувати варіаційний ряд:
![]() 1 4 5 7 12
1 4 5 7 12
![]() 2 5 3 4 6 .
2 5 3 4 6 .
Об’єм
вибірки дорівнює
![]() .
Оскільки у вибірці з 20 спостережень
одні й ті ж самі значення зустрічаються
по декілька разів, то приріст функції
.
Оскільки у вибірці з 20 спостережень
одні й ті ж самі значення зустрічаються
по декілька разів, то приріст функції
![]() у відповідних точках
у відповідних точках
![]() буде пропорційним до кратності цих
точок, тобто
буде пропорційним до кратності цих
точок, тобто
![]()
![]()
Незміщена оцінка. Оцінка
 деякого невідомого параметра
деякого невідомого параметра називаєтьсянезміщеною,
якщо
називаєтьсянезміщеною,
якщо
 .
Незміщеною оцінкою для
.
Незміщеною оцінкою для є вибіркове середнє
є вибіркове середнє .
Якщо
.
Якщо відомо, то незміщеною оцінкою для
відомо, то незміщеною оцінкою для є
є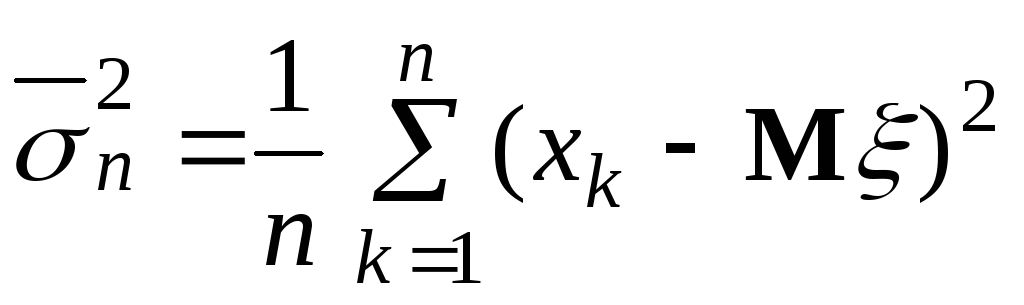 .
Якщо ж
.
Якщо ж невідомо, то незміщеною оцінкою для
невідомо, то незміщеною оцінкою для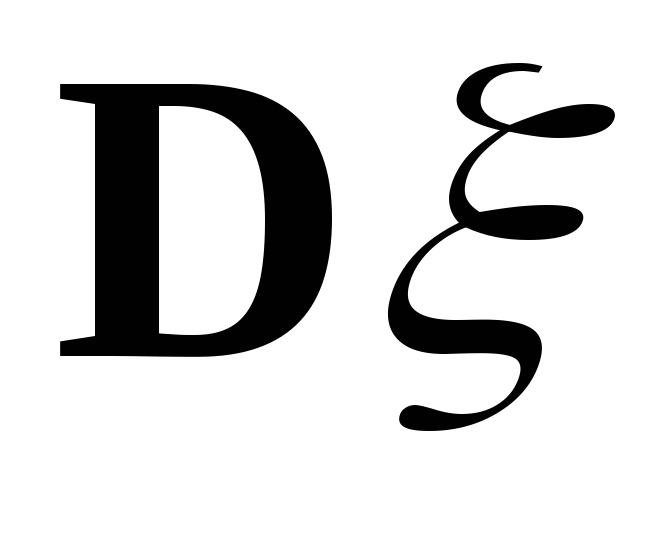 є
є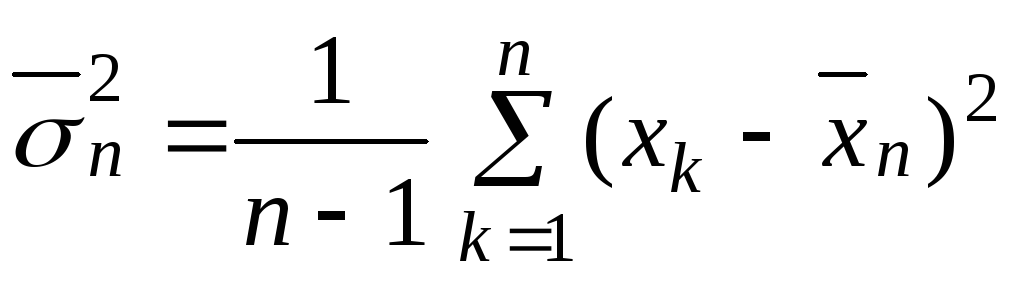 .
.
Приклад
2.
В
результаті експерименту була отримана
вибірка з
![]() спостережень:
спостережень:
![]() 2 5 9 11 15 20
2 5 9 11 15 20
![]() 7 15 16 21 12 9
7 15 16 21 12 9
Знайти незміщене значення середнього.
Розв’язання. Незміщена оцінка математичного сподівання знаходиться за формулою:
![]()
де
![]() – це кількість різних значень
– це кількість різних значень![]() ,
що спостерігались (у даному прикладі
,
що спостерігались (у даному прикладі![]() ).
).
Приклад
3.
Для
визначення точності вимірювального
приладу, систематична похибка якого
практично дорівнює нулю, було зроблено
п’ять незалежних вимірювань, які дали
такі результати:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() м. Визначити незміщену оцінку дисперсії
похибки вимірювального приладу, якщо
значення величини, що вимірюється:a)
відомо і дорівнює
м. Визначити незміщену оцінку дисперсії
похибки вимірювального приладу, якщо
значення величини, що вимірюється:a)
відомо і дорівнює
![]() м;b)
невідомо.
м;b)
невідомо.
Розв’язання.
Розглянемо спочатку випадок, коли відомо
![]()
![]() .
Тоді незміщену оцінку
.
Тоді незміщену оцінку![]() дисперсії знаходимо за формулою
дисперсії знаходимо за формулою
![]() .
.
Якщо ж точне значення величини, що вимірюється, невідоме, то будуємо спочатку вибіркове середнє
![]() .
.
Незміщену
оцінку![]() дисперсії знаходимо за формулою
дисперсії знаходимо за формулою
![]() .
.
Метод найбільшої правдоподібності. Нехай за спостереженнями випадкової величини
 із щільністю розподілу
із щільністю розподілу була отримана вибірка
була отримана вибірка ,
де
,
де – невідомий параметр. Припустимо, що
функція
– невідомий параметр. Припустимо, що
функція диференційована за
диференційована за .
Оцінка параметра
.
Оцінка параметра будується з умови максимізаціїфункції
правдоподібності
будується з умови максимізаціїфункції
правдоподібності
![]() ,
,
тобто оцінка задовольняє рівняння правдоподібності
![]() або
або
![]() .
.
Дискретний
випадок.
Припустимо, що випадкова величина
![]() приймає значення
приймає значення![]() з ймовірностями
з ймовірностями![]() ,
де
,
де![]() – невідомий параметр. Спостерігається
вибірка
– невідомий параметр. Спостерігається
вибірка![]() ,
в яку значення
,
в яку значення![]() входить
входить![]() разів,
разів,![]() .
Ймовірність отримання саме цієї вибірки
(з точністю до постійного множника)
визначаєтьсяфункцією
правдоподібності
.
Ймовірність отримання саме цієї вибірки
(з точністю до постійного множника)
визначаєтьсяфункцією
правдоподібності
![]() .
.
Оцінка
![]() є розв’язком рівняння
правдоподібності
є розв’язком рівняння
правдоподібності
![]() .
.
Приклад
4.
Відомо, що випадкова величина
![]() має рівномірний розподіл на
має рівномірний розподіл на![]() .В
результаті експерименту була отримана
вибірка з
.В
результаті експерименту була отримана
вибірка з
![]() спостережень:
спостережень:
