
- •Т е о р і я й м о в і р н о с т е й т а
- •03056, Київ-56, просп. Перемоги, 37 Зміст
- •1. Елементи комбінаторики
- •2. Біноміальні тотожності
- •3. Формула включень та виключень
- •4. Класичне означення ймовірності
- •5. Геометричний метод знаходження ймовірності
- •6. Умовні ймовірності, незалежні події, формула повної ймовірності, формула Байєса
- •Дискретні випадкові величини, математичне сподівання та дисперсія
- •Загальне поняття випадкової величини, функції від випадкових величин
- •Граничні теореми
- •0.74 1.12 3.75 4.33 5.71 6.09 7.89 8.03 9.55 10.22.
- •Список використаної літератури
6. Умовні ймовірності, незалежні події, формула повної ймовірності, формула Байєса
Умовна ймовірність. Умовна ймовірність випадкової події
 при умові, що відбулась подія
при умові, що відбулась подія
 ,
,
 визначається за формулою
визначається за формулою
![]() (20)
(20)
Незалежні
події. Випадкові
події
![]() і
і
![]() називаються
незалежними, якщо
називаються
незалежними, якщо
![]()
Незалежні
у сукупності події. Випадкові
події
![]() називаються незалежними у сукупності,
якщо для будь-якого
називаються незалежними у сукупності,
якщо для будь-якого![]() і для будь-яких
і для будь-яких![]() виконується рівність
виконується рівність

Приклад
1.
Три
попарно незалежні події
![]() одночасно відбутися не можуть. У
припущенні, що всі вони мають одну й ту
ж саму ймовірність
одночасно відбутися не можуть. У
припущенні, що всі вони мають одну й ту
ж саму ймовірність![]() ,
визначити максимально можливе значення
,
визначити максимально можливе значення![]() .
.
Розв’язання.
Позначимо
![]() Очевидно
Очевидно![]() – це монотонно неспадна функція за
– це монотонно неспадна функція за![]() .
Використовуючи формулу включень та
виключень (16), маємо
.
Використовуючи формулу включень та
виключень (16), маємо
![]()
![]()
(було
враховано, що події попарно незалежні,
але всі вони одночасно відбутися не
можуть). Ця функція монотонно зростає
на проміжку
![]() і досягає свого максимуму при
і досягає свого максимуму при![]() .
Саме ця точка і задовольняє умову задачі.
.
Саме ця точка і задовольняє умову задачі.
Приклад
2.
Гравці
![]() та
та![]() грають у шахи. За виграш партії
зараховується одне очко. Ймовірність
того, що партію виграє гравець
грають у шахи. За виграш партії
зараховується одне очко. Ймовірність
того, що партію виграє гравець![]() дорівнює
дорівнює![]() ,
а гравець
,
а гравець![]() –
відповідно
–
відповідно
![]() (нічия вважається неможливою). Всю гру
виграє той, хто обжене суперника на 2
очка. Знайти ймовірність виграшу для
гравця
(нічия вважається неможливою). Всю гру
виграє той, хто обжене суперника на 2
очка. Знайти ймовірність виграшу для
гравця![]() .
.
Розв’язання.
Розглянемо можливі варіанти розвитку
гри, у яких виграє гравець
![]() .
По-перше, має бути зіграно обов’язково
парну кількість партій, причому останні
дві з них повинен виграти гравець
.
По-перше, має бути зіграно обов’язково
парну кількість партій, причому останні
дві з них повинен виграти гравець![]() (загальну кількість зіграних партій
позначимо
(загальну кількість зіграних партій
позначимо![]() ).
По-друге, якщо розглянути партії
).
По-друге, якщо розглянути партії![]() та
та![]()
![]() ,
то одну з них виграє гравець
,
то одну з них виграє гравець![]() ,
а другу – гравець
,
а другу – гравець![]() .
Враховуючи, що у серії з
.
Враховуючи, що у серії з![]() партій гравець
партій гравець![]() виграє
виграє![]() партій, а гравець
партій, а гравець![]() –
–![]() партій, а також те, що результати партій
є подіями незалежними у сукупності,
отримуємо ймовірність
партій, а також те, що результати партій
є подіями незалежними у сукупності,
отримуємо ймовірність![]() виникнення серії з
виникнення серії з![]() партій, результатом якої є виграш гравця
партій, результатом якої є виграш гравця![]() .
Легко бачити, що кількість таких серій
з
.
Легко бачити, що кількість таких серій
з![]() партій дорівнює
партій дорівнює![]() (у кожних двох партіях може спочатку
виграти
(у кожних двох партіях може спочатку
виграти![]() ,
а потім
,
а потім![]() ,
або навпаки – спочатку
,
або навпаки – спочатку![]() ,
а потім
,
а потім![]() ).
Враховуючи всі можливі значення
).
Враховуючи всі можливі значення![]() ,
маємо остаточну відповідь
,
маємо остаточну відповідь
![]()
Приклад
3.
Три
мисливці одночасно зробили по одному
пострілу у ведмедя. Ведмедя вбито однією
кулею. Яка ймовірність того, що ведмедя
вбито першим, другим або третім мисливцем,
якщо ймовірності влучення для них
дорівнюють відповідно
![]() ,
,![]() ,
,![]() ?
?
Розв’язання.
Введемо події
![]() {
{![]() -й
мисливець влучив у ведмедя},
-й
мисливець влучив у ведмедя},
![]() .
Тоді
.
Тоді![]() {ведмедя
вбито однією кулею}
{ведмедя
вбито однією кулею}
![]()
![]() ,
де
,
де![]() позначає подію, протилежну до
позначає подію, протилежну до![]() .
Згідно з умовою задачі треба обчислити
ймовірності
.
Згідно з умовою задачі треба обчислити
ймовірності![]() Враховуючи незалежність подій
Враховуючи незалежність подій![]() ,
маємо
,
маємо
![]()
Тоді згідно з (20)
![]()
Аналогічно
![]()
Повна група подій. Випадкові події
 утворюють повну групу подій, якщо
виконані умови:
утворюють повну групу подій, якщо
виконані умови:
1)
![]() – попарно несумісні, тобто
– попарно несумісні, тобто![]() Ø
для будь-яких
Ø
для будь-яких![]()
2)
![]()
Формула
повної ймовірності. Якщо
![]() – повна група подій і
– повна група подій і![]() то для будь-якої випадкової події
то для будь-якої випадкової події![]() виконується рівність
виконується рівність
![]() (21)
(21)
Приклад 4. З урни, що містить 6 білих та 4 чорних кулі, беруть послідовно дві кулі та перекладають їх в урну, що містить 2 білі та 4 чорні кулі. Чому дорівнює ймовірність витягнути білу кулю з другої урни?
Розв’язання. Введемо повну групу подій:
![]() {у
другу урну переклали дві білих кулі};
{у
другу урну переклали дві білих кулі};
![]() {спочатку
переклали білу, а потім чорну кулі};
{спочатку
переклали білу, а потім чорну кулі};
![]() {спочатку
переклали чорну, а потім білу кулі};
{спочатку
переклали чорну, а потім білу кулі};
![]() {у
другу урну переклали дві чорні кулі}.
{у
другу урну переклали дві чорні кулі}.
Визначимо ймовірності цих подій:
![]()
В той же час
![]()
![]()
Згідно з формулою повної ймовірності (21) маємо
![]()
Приклад
5.
Два гравці
![]() і
і![]() по черзі стріляють у ціль. Виграє той,
хто влучить перший. Ймовірність влучення
в ціль для
по черзі стріляють у ціль. Виграє той,
хто влучить перший. Ймовірність влучення
в ціль для![]() і
і![]() дорівнюють відповідно
дорівнюють відповідно![]() і
і![]() .
Перший стріляє
.
Перший стріляє![]() .
Обчислити ймовірність виграшу для
кожного з гравців.
.
Обчислити ймовірність виграшу для
кожного з гравців.
Розв’язання.
Позначимо через
![]() та
та![]() ймовірності виграшу відповідних гравців.
Введемо повну групу подій:
ймовірності виграшу відповідних гравців.
Введемо повну групу подій:
![]() {ціль
була уражена при
{ціль
була уражена при
![]() -му
пострілі},
-му
пострілі},
![]()
Розглянемо два випадки.
 Тоді
Тоді
![]()
 Тоді
Тоді
![]()
Тому згідно з (21) маємо
![]()
Аналогічно
![]()
Формула Байєса. Якщо
 – повна група подій і
– повна група подій і то для будь-якої випадкової події
то для будь-якої випадкової події такої, що
такої, що виконується рівність
виконується рівність
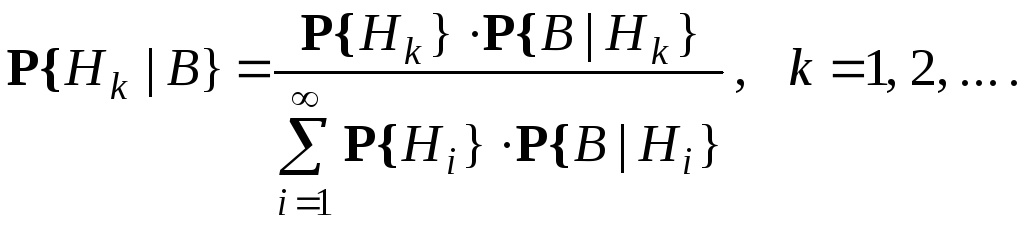 (22)
(22)
Приклад 6. Передається повідомлення, яке закодоване нулями та одиницями. При передачі можуть виникати помилки: одиниця сприймається як нуль з ймовірністю 0.1, а нуль як одиниця – з ймовірністю 0.2. Відомо, що у повідомленні 40% символів складають одиниці. Знайти ймовірність того, що навмання взятий символ було передано без помилки, якщо: a) прийнято одиницю; b) прийнято нуль.
Розв’язання.
Введемо події:
![]() {передано
одиницю},
{передано
одиницю},![]() ={передано нуль},
={передано нуль},![]() {прийнято
одиницю}. Потрібно знайти ймовірність
{прийнято
одиницю}. Потрібно знайти ймовірність![]() Використаємо формулу Байєса. Для цього
визначимо всі ймовірності, що входять
у праву частину формули (22). З умови
задачі випливає, що
Використаємо формулу Байєса. Для цього
визначимо всі ймовірності, що входять
у праву частину формули (22). З умови
задачі випливає, що![]() Оскільки
Оскільки![]() то
то![]() Крім того,
Крім того,![]() Згідно з формулою (22) отримуємо
Згідно з формулою (22) отримуємо
![]()
У
випадку b)
позначимо
![]() {прийнято
нуль}.
Тоді
{прийнято
нуль}.
Тоді
![]()
![]() Тоді
Тоді
![]()
Приклад 7. З 18 стрільців п’ятеро потрапляють у мішень з ймовірністю 0.8, семеро – з ймовірністю 0.7, четверо – з ймовірністю 0.6 та двоє – з ймовірністю 0.5. Навмання обраний стрілець робить постріл, але у мішень не влучає. До якої з цих чотирьох груп найбільш ймовірно належить стрілець?
Розв’язання.
Розіб’ємо 18 стрільців на чотири групи
згідно з вказаними ймовірностями
влучення. Введемо події:
![]() {навмання
обраний стрілець належить
{навмання
обраний стрілець належить![]() -й
групі},
-й
групі},![]() {стрілець
не влучає у мішень}. Потрібно обчислити
і порівняти ймовірності
{стрілець
не влучає у мішень}. Потрібно обчислити
і порівняти ймовірності![]()
![]() Оскільки стрільця обрано навмання, то
Оскільки стрільця обрано навмання, то
![]()
Крім того, обчислюємо відповідні умовні ймовірності
![]()
Далі застосовуємо формулу Байєса (22):

Аналогічно
![]() Звідси випливає, що найбільш ймовірно
стрільця було обрано з другої групи.
Звідси випливає, що найбільш ймовірно
стрільця було обрано з другої групи.
Приклад
8.
З урни, що містить
![]() білих
білих![]() і
і![]() чорних куль, загублено одну кулю. Для
того, щоб визначити склад куль в урні,
з урни взяли дві кулі, які виявились
білими. Знайти ймовірність того, що
загублена куля – біла.
чорних куль, загублено одну кулю. Для
того, щоб визначити склад куль в урні,
з урни взяли дві кулі, які виявились
білими. Знайти ймовірність того, що
загублена куля – біла.
Розв’язання.
Введемо події:
![]() {загублена
куля є білою},
{загублена
куля є білою},![]() {загублена
куля є чорною},
{загублена
куля є чорною},![]() {з
урни взяли дві білих кулі}. Потрібно
обчислити ймовірність
{з
урни взяли дві білих кулі}. Потрібно
обчислити ймовірність![]() Оскільки в урні було
Оскільки в урні було
![]() білих і
білих і![]() чорних куль, то безумовні ймовірності
подій
чорних куль, то безумовні ймовірності
подій![]() та
та![]() визначаються таким чином:
визначаються таким чином:
![]() В той же час
В той же час
![]()
Підставляючи ці значення у формулу (22), маємо
![]()
