Разбор варианта контрольной работы

Задача №1 составлена на тему «Элементы комбинаторики». За­дача решается непосредственным применением правила произведения или суммы. Важно понять, как именно происходит выбор того или иного объекта, важен ли порядок выбора или нет.

Пример: Игральный кубик бросают трижды. Сколько разных последовательностей цифр можно при этом получить?

Мы три раза подбрасываем кубик и следим, какая цифра выпа­ла. Каждый раз у нас есть шесть вариантов: 1, 2, 3, 4, 5 или 6. При этом нам важно, какая цифра выпадает в какой последовательности. Так наборы 3, 4, 5 и 4, 3, 5 для нас различны. По правилу произведе­ния имеем 6•6•6 = 216.

Задача №2 на прямое применение определения вероятности со­бытия, как отношения числа благоприятствующих событию исходов к общему числу исходов.

Пример: Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4.

Посчитаем общее количество исходов нашего испытания. На одной из костей может выпасть любое количество очков от 1 до 6 и на второй кости так же шесть вариантов, то есть всего по правилу произ­ведения 6•6 = 36 исходов.

Посчитаем количество благоприятных исходов. Их всего 3: на первой кости 1, а на второй кости 3 очка; наоборот, на первой кости 3, а на второй 1 очко; на обеих костях по два очка. А значит, вероятность выпадения четырех очков равна:

3 1

P= =

36 12

В задачах №3 и №4 важно понять на какие более мелкие собы­тия разбивается данное событие, и как эти события связаны: должно быть одновременное выполнение их (союз «и»), или важно выполне­ние одного из них (союз «или»). После чего, следует применить фор­мулу вероятности суммы или произведения.

Пример: Три команды А₁, А₂, Аз спортивного общества А со­стязаются соответственно с тремя командами общества В. Веро­ятности того, что команды общества А выиграют у команд обще­ства В, таковы: при встрече А₁ с В₂ — 0,8; А₂ с В₂ — 0,4; Аз с Вз — 0,4. Для победы необходимо выиграть не менее двух матчей из трех. (Ни­чьи во внимание не принимаются). Победа какого из обществ вероят­нее?

Для того чтобы ответить на вопрос задачи, нужно знать какова вероятность победы каждого из обществ. Заметим, что победа одного

из обществ означает поражение для второго, т. е. события: А - побе­дило общество А и В — победило общество В - являются противопо­ложными, а значит сумма их вероятностей равна единице. Нам доста­точно найти вероятность одного из этих событий, пусть А.

Для того, чтобы произошло событие А, общество А должно по­бедить по крайней мере в двух матчах, т. е. в двух или в трех. Пусть событие А₁ - общество А₁ победило у общества В₁; событие А₂ - об­щество А₂ победило у общества В₂; событие А₃ - общество А₃ побе­дило у общества В₃. Тогда событие А можно представить в виде:

А= А₁ • А₂• А₃ + А₁ • А₂ • А₃ + А₁ • А₂ • А₃ + А₁• А₂• А₃

События А₁ • А₂ • А₃; А₁ • А₂ • А₃; А₁ • А₂ • А₃; А₁ • А₂ • А₃ являются несо­вместными, поэтому вероятность их суммы равна сумме вероятно­стей. А события А₁, А₂ и А₃ являются независимыми. Поэтому:

Р(А) = Р(А₁) • Р(А₂) • Р(А₃) + Р(А₁) • Р(А₂) • Р(А3) + Р(А₁) • Р(А₂) • Р(А₃)+

+ Р(А₁) • Р(А₂) • Р(А₃ ) = 0,8 • 0,4 • 0,4 + 0,8 • 0,4 • (1 - 0,4) + 0,8 • (1 - 0,4) • 0,4+

+ (1-0,8)•0,4•0,4 = 0,544

Тогда Р(В) = 1- Р(А) = 1-0,544 = 0,456. То есть победа общества А

более вероятна.

Задача №5 на применение формулы полной вероятности. Важ­но понять вероятность какого события надо найти, и от каких событий вероятность искомого события зависит.

Пример: В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке 10 радиоламп, из 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартная.

Нам требуется найти вероятность события А - лампа, наудачу извлеченная из первой коробки стандартная. Это событие зависит от того, какую лампу - стандартную или нестандартную - мы переложи­ли из второй коробки в первую. Пусть событие В1 - из второй коробки

в первую переложили стандартную деталь; В₂ - из второй коробки в первую переложили нестандартную деталь. События В1 и В₂ несо­вместны и образуют полную группу событий, то есть мы находимся в условиях формулы полной вероятности.

9 19 1 18 189

Р(А) = Р(В₁)-Р_В1(А) + Р(В₂)•Р_В2(А) = ­ •­­ + ­ • ­ = ­­ =0,9

10 21 10 21 210

Задача №6 на тему «Математическое ожидание дискретной случайной величины».

Пример: 2 стрелка делают по одному выстрелу в одну мишень. Вероятности попадания для первого стрелка при одном выстреле —

0,5, для второго — 0,4. Дискретная случайная величина X — число по­паданий в мишень. Найти закон распределения и математическое ожидание величины X.

Наша дискретная величина может принимать 3 значения: 0 -никто не попал, 1 - один попал, а второй нет, 2 - оба стрелка попали. Составим закон распределения:

X	0	1	2
P	(1-0,5)•(1-0,4)=0,3	1-0,3-0,2=0,5	0,4•0,5=0,2

Математическое ожидание равно:

М(Х) = 0 • 0,3 +1 • 0,5 + 1 • 0,5+2 • 0,2 = 0,9.

Задача №7 на тему «Функция распределения случайной вели­чины».

Пример: Дискретная случайная величина задана таблицей рас­пределения:

X	1	4	8
P	0,3	0,1	0,6

Найти функцию распределения и начертить ее график.

Если x ≤1, то F(х)= 0 (четвертое свойство). Если 1 ≤ х ≤ 4, то

F(х) = 0,3. Действительно X может принять значение 1 с вероятно­стью 0,3. Если 4 < х ≤ 8, то F(х) = 0,4, как сумма 0,3+0,1. Если х > 8,

то F(х) =1. Так как событие X ≤ 8 является достоверным.

Итак функция распределения аналитически может быть записа­на как:

0, при х≤1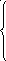

F(х)=

0,3, при 1<х≤4

0,4,при 4<х≤8 1,при х>8

1