
termh_z
.pdf
Кинетическая энергия точки |
|
есть |
|
, |
|
|
|||||
а ее потенциальная энергия |
2 |
|
|
2 |
|
|
|
||||
Координаты |
и |
точки |
запишутся следующим.образом: |
|
|||||||
Отсюда следует, что |
|
|
|
, |
|
|
. |
. |
|||
Кинетическая и потенциальная,энергии точки |
|
|
равны |
||||||||
2 |
|
|
2 |
|
2 |
cos |
, |
||||
Функция Лагранжа всей системы |
. |
|
|||||||||
|
cos |
|
|
|
|
2 |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
||
Уравнений Лагранжа в данной задаче будет два:
0, 0.
Производя дифференцирование, находим:
cos |
cos |
sin |
0, |
sin |
0. |
■ |
Задача 3.5. Составьте уравнения движения частицы, движущейся по абсолютно гладкой поверхности вертикального цилиндра радиуса в однородном поле тяжести.
□ Данную задачу удобно решать в цилиндрической системе координат. Начало отсчета системы выберем в центре нижнего основания цилиндра, а
21

ось направим вертикально вверх. За ноль потенциальной энергии примем нижнее основание цилиндра. В качестве обобщенных координат возьмем координаты ϕ и .
Кинетическая и потенциальная энергии точки запишутся в виде:
Функция Лагранжа |
2 |
|
|
|
|
|
, |
|
|
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
а уравнения Лагранжа по |
переменным ϕ |
и |
|
есть: |
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
■ |
|
|
Задача 3.6. Покажите, что |
уравнения Лагранжа (3.1) не изменяются, если |
||||||||||||||
|
0, |
|
|
|
|
0. |
|
|
|
||||||
вместо функции |
, , |
взять функцию |
|
|
|
, |
|
|
|||||||
|
|
|
|
, , |
|
|
|
|
, |
, |
|
|
, |
|
|
где |
– произвольная дважды непрерывно дифференцируемая функция |
||||||||||||||
координат, |
и времени. |
|
|
|
|
|
|
|
|
|
|
|
|
, по времени: |
|
□ Запишем выражение для полной производной функции |
|||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
β |
|
. |
|
|
|
|
|
|
|
|
β |
|
β |
|
|
|
||||
Из этого равенства можно получить два соотношения:
|
|
|
|
|
β |
|
, |
3.5 |
α |
|
|
β |
β α |
α |
. 3.6
αα
Используя равенство (3.6), находим:
|
|
|
|
|
β |
|
. |
3.7 |
α |
|
|
β |
α β |
α |
22

В силу того, что функция |
|
|
|
, |
|
|
|
|
дважды |
непрерывно |
|||||||||||||||||||||||||
дифференцируемая, можно изменить порядок |
ее |
дифференцирования по |
|||||||||||||||||||||||||||||||||
переменным α, |
β, и записать соотношение (3.7) в виде |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
. |
|
3.8 |
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
β |
β |
α |
|
|
|
|
|
α |
|||||||||||
Подставляя |
|
функцию |
|
|
, , |
|
в |
(3.1) |
|
и |
учитывая |
(3.5) и (3.8), |
|||||||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|||||
|
|
|
|
α |
|
|
|
|
α |
|
|
|
|
α |
β |
|
β |
α |
|
|
α |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
0. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
α |
β |
|
|
|
β |
α |
|
|
|
|
|
|
α |
|
|
|||||||||||
Отсюда имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0,
αα
что совпадает с уравнением Лагранжа для функции . ■
Задачи для самостоятельного решения
12. Напишите функцию Лагранжа свободной материальной точки массы в
цилиндрических координатах. |
|
|
13. Длина математического маятника изменяется по закону |
. Найдите |
|
функцию Лагранжа и уравнение движения маятника. |
|
|
14. Два математических маятника одинаковой длины |
связаны между собой |
|
пружиной жесткости , закрепленной на расстоянии |
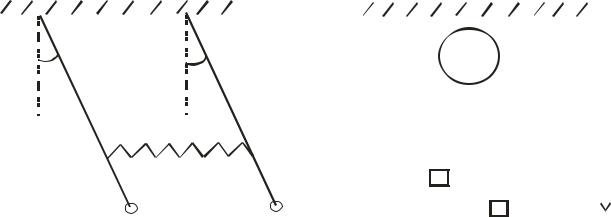
от точки подвеса |
|
(рис. 3.2). Найдите функцию и уравнения Лагранжа для данной системы, считая углы отклонения маятников от положения равновесия малыми.
15. Две точки с массами и соединены невесомой и нерастяжимой нитью, перекинутой через гладкий неподвижный блок (рис. 3.3). Найдите функцию Лагранжа и уравнение движения грузов.
23
16. Через гладкий неподвижный блок перекинута невесомая и нерастяжимая нить, к одному из концов которой привязан груз массы . На другом конце повис человек массы , который, выбирая веревку, поднимает груз, оставаясь при этом на одном и том же расстоянии от Земли. Найдите функцию Лагранжа системы и уравнение движения груза .
17. Точка подвеса математического маятника движется в вертикальном
направлении по закону |
2 |
( |
). Найдите функцию Лагранжа и |
уравнение движения маятника. |
|
|
18.Точка подвеса математического маятника движется по горизонтали по закону . Найдите функцию Лагранжа и уравнение движения маятника.
19.Точка подвеса математического маятника равномерно движется в
вертикальной плоскости по окружности радиуса с угловой скоростью ω. Найдите функцию Лагранжа и уравнение движения маятника.
|
ϕ |
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
2 |
a |
|
|
|
|
|
|
|
|
||||
|
a |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
m1 |
|
|
m2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
|
Рис. 3.2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Рис. 3.3 |
|
|
|||||
§ 4. Уравнения Лагранжа при наличии диссипативных и электромагнитных сил
До сих пор мы рассматривали механические системы с голономными идеальными связями при наличии потенциальных сил. Для таких систем функция Лагранжа . Запишем теперь функцию Лагранжа при наличии:
1)диссипативных сил, а именно сил сопротивления, пропорциональных скорости частицы;
2)электромагнитных сил.
24
1) Диссипативные силы. В случае если на частицу массы |
действует сила |
|||||||||||
сопротивления |
вида |
( |
|
- коэффициент пропорциональности) |
||||||||
функцию Лагранжа можно представить в виде |
, |
, |
|
4.1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
где |
|
- потенциальная энергия, |
действующих на частицу потенциальных |
|||||||||
, |
2 |
|
|
|
|
|
||||||
сил. |
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4.1. Покажите, что уравнения Лагранжа с функцией |
вида (4.1) |
|||||||||||
приводят |
к |
уравнению |
|
|
, |
|
описывающему |
движение |
||||
материальной точки при наличии диссипативной силы |
|
и |
||||||||||
потенциальной силы . |
|
|
|
|
|
|
|
|
|
|||
□ Сначала найдем, что
,
и, следовательно,
.
Производная от функции (4.1) по равна
.
Но |
есть по определению сила . |
С учетом этого уравнение Лагранжа принимает вид:
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
Сокращая обе части этого уравнения на |
|
и перенося последние два члена |
||||||||||
|
||||||||||||
вправо, получим искомое уравнение движения:
.
■
25

Задача 4.2. Материальная точка массы движется по параболе, расположенной вертикально в поле тяжести. На точку действует сила сопротивления, пропорциональная ее скорости с коэффициентом пропорциональности . Найдите функцию Лагранжа и уравнение движения точки.
□ Направим ось вертикально вверх, и пусть уравнением параболы будет
|
|
|
, |
0, |
. |
4.2 |
|
|
|
||||
В качестве обобщенной |
координаты выберем |
. |
|
|||
2 |
|
|
|
|||
Квадрат скорости точки равен
. 4.3
Дифференцируя (4.2) по времени, находим:
.
Подставляя это выражение в (4.3), получим:
.
Кинетическая энергия точки
2 |
2 |
, |
а ее потенциальная энергия определяется выражением:
2 .
В соответствии с формулой (4.1) составляем функцию Лагранжа:
2 |
|
1 |
. |
|
Наконец, пользуясь формулой (3.1), запишем уравнение Лагранжа по переменной :
1 |
0. |
■
26
2) Электромагнитные силы. Пусть частица находится в электрическом поле напряженности и в магнитном поле напряженности . Напряженности электрического и магнитного полей могут быть выражены через скалярный φ и векторный потенциалы:
1 |
|
|
φ |
|
|
|
|
, |
4.4 |
|
|
|||
|
, |
4.5 |
||
где - скорость света. В прямоугольной декартовой системе координат операции градиент и ротор записываются в виде:
φ |
φ |
|
φ |
|
φ |
|
φ |
, |
4.6 |
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
, |
4.7 |
|
|
|
|
|
|
|
||||||||
– орты прямоугольной системы координат, а |
- |
|||||||||||||
проекции, |
вектора, |
на оси координат. С учетом (4.6) и (4.7) |
,запишем, |
|||||||||||
уравнения (4.4) и (4.5) в проекциях на оси прямоугольной декартовой системы координат:
1 |
|
|
|
|
φ |
, |
1 |
|
|
|
|
|
φ |
, |
1 |
|
|
|
|
φ |
, 4.8 |
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
, |
|
|
|
|
, |
|
|
|
|
. |
4.9 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
С помощью скалярного и векторного потенциалов функцию Лагранжа частицы массы и заряда , находящейся в электромагнитном поле, можно записать следующим образом:
, , , φ. 4.10 2
27
Задача 4.3. Покажите, что уравнение движения
|
|
|
4.11 |
|
|
||
частицы массы |
и заряда , находящейся в электромагнитном поле (см. |
||
задачу 1.3), получается из уравнений Лагранжа, в которых в качестве функции Лагранжа взята функция (4.10).
□ Составим уравнения Лагранжа для функции (4.10). Сначала найдем, что
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ |
. |
4.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Аналогичные соотношения имеют место для переменных |
|
. Подстановка |
||||||||||||||||||||||||
(4.12) в уравнение Лагранжа по переменной , т.е. в |
уравнение |
|
|
|
|
|||||||||||||||||||||
|
|
|
и |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
приводит к равенству |
|
|
|
|
|
|
|
|
||||||||||||||||||
φ0.
Перенося в этом уравнении все силы в правую часть и группируя слагаемые, получаем:
|
|
|
|
|
φ |
|
|
|
. |
4.13 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С учетом формул (4.8) и (4.9) замечаем, что первые два члена в правой |
||||||||||||||||||||
части (4.13) есть умноженная на заряд проекция |
вектора напряженности |
|||||||||||||||||||
электрического поля на ось , а в круглых скобках стоят проекции |
и |
|||||||||||||||||||
вектора напряженности магнитного поля на оси |
и |
, соответственно. |
||||||||||||||||||
Теперь уравнение (4.13) можно переписать в виде |
|
|
|
|||||||||||||||||
|
|
. |
|
|
|
|
|
4.14 |
||||||||||||
|
|
|
|
|
|
|||||||||||||||
28

Абсолютно аналогично можно получить уравнения Лагранжа для переменных и :
, 4.15
. 4.16
Вспоминая определение векторного произведения, видим, что в круглых скобках равенств (4.14)-(4.16) стоят проекции векторного произведения , и, следовательно, уравнения Лагранжа (4.14)-(4.16) эквивалентны уравнению (4.11). ■
Задача 4.4. Найдите в цилиндрических координатах функцию Лагранжа и уравнения движения частицы массы и заряда , находящейся в однородном магнитном поле , если векторный потенциал задан в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
□ Направим ось |
|
цилиндрической |
системы координат вдоль вектора |
. В |
|||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
цилиндрических координатах радиус-вектор |
|
|
|
|
|
||||||||||||||||||||||||||
Векторный потенциал |
1 |
|
|
|
|
|
. |
1 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
0 |
|
|
2 |
|
|
. |
4.17 |
||||
Учитывая (4.17) и то, что в |
0цилиндрической системе координат |
||||||||||||||||||||||||||||||
проекция скорости |
|
|
|
|
|
|
|
|
|
|
(см. приложение), |
находим функцию Лагранжа, |
|||||||||||||||||||
в которой в качестве обобщенных координат выступают переменные , |
, : |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||
Теперь |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|||||||||||||||||
|
составим уравнения Лагранжа: |
|
|
0, |
|
|
|
4.18 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
2 |
|
0, |
|
4.19 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
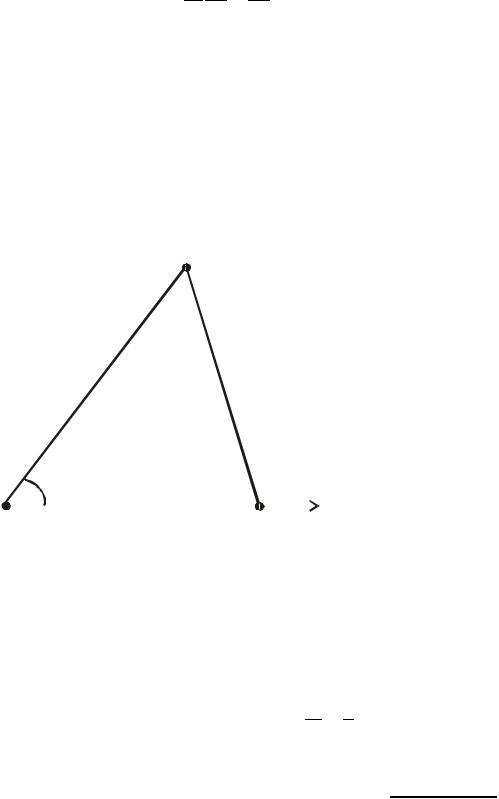
0. 4.20
Уравнения (4.18)-(4.20) есть искомые уравнения движения точки. Отметим, что векторный потенциал однородного магнитного поля всегда можно
представить в |
виде |
1 |
|
|
|
. Другой |
способ |
задания |
векторного |
|||||||||||
потенциала однородного магнитного поля приведен в задаче 22. ■ |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Задача 4.5. Найдите функцию Лагранжа для частицы массы |
|
и заряда , |
||||||||||||||||||
находящейся в поле электрического диполя. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
□ |
Электрическим |
диполем |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
называется |
система |
из |
двух |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равных по абсолютной величине |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
противоположных |
по |
знаку |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
электрических зарядов |
|
|||||
|
|
|
r |
|
|
|
|
|
|
r’ |
|
|
|
, расстояние |
|
между |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 и |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которыми мало по сравнению с |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расстоянием до рассматриваемых |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точек поля (в которых находится |
||||||
|
|
|
θ |
|
|
|
|
|
|
|
|
|
|
частица). |
|
Схематично |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
рассматриваемая |
|
система |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
-e |
|
|
|
a |
|
e |
|
z изображена на рис. 4.1. |
|
|||||||||||
|
|
|
|
Рис. 4.1 |
|
|
|
|
|
|
Пусть |
и |
– расстояния |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
до частицы от зарядов |
|
, соответственно. Направим полярную ось (ось |
||||||||||||||||||
на рисунке) сферической системы координат вдоль диполя, а начало отсчета |
|||||||||
и |
|
|
|
|
|
|
|
|
|
совместим с зарядом . |
|
|
|
|
|
|
|
|
|
Потенциал диполя в точке нахождения заряда равен |
|
|
|
||||||
|
φ |
|
1 |
1 |
. |
|
|
|
4.21 |
Выразим с помощью теоремы косинусов |
через и θ: |
|
|
|
|
||||
|
|
|
|
|
|
|
θ |
|
|
В равенстве (4.22) мы пренебрегли членом |
θ |
|
|
|
. |
||||
, поскольку по условию |
|||||||||
|
|
2 |
|
|
|
2 |
|
. |
4.22 |
30
