
MU_LR_VychMat_230400
.pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тульский государственный университет»
Кафедра Автоматики и телемеханики
СБОРНИК МЕТОДИЧЕСКИХ УКАЗАНИЙ
К ЛАБОРАТОРНЫМ РАБОТАМ
по дисциплине
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Направление подготовки: 230400 «Информационные системы и технологии» Профиль : «Информационные системы»
Формы обучения: очная
Тула 2012 г.
Методические указания к лабораторным работам составлены доцентом,
к.ф.-м.н. Сулимовой В.В. и обсуждены на заседании кафедры автоматики и телемеханики факультета кибернетики,
протокол № 6 от " 31 " января 2012 г.
Зав. кафедрой________________А.А. Фомичев
Методические указания к лабораторным работам пересмотрены и утверждены на заседании кафедры автоматики и телемеханики факультета
кибернетики,
протокол №___ от "___"____________ 20___ г. Зав. кафедрой________________А.А. Фомичев
2
СОДЕРЖАНИЕ |
|
1. ЗАНЯТИЕ 1. ПРИБЛИЖЕННЫЕ ЧИСЛА И ИХ ПОГРЕШНОСТИ ......................................................... |
5 |
1.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ .............................................................................................................................. |
5 |
1.1.1. Виды погрешностей................................................................................................................................. |
5 |
1.1.2. Верные и сомнительные значащие цифры приближенного числа ...................................................... |
6 |
1.1.3. Связь между количеством верных цифр и относительной погрешностью числа ............................ |
7 |
1.1.4. Погрешности при вычислении значений функций................................................................................. |
8 |
1.1.5. Погрешности операций над приближенными числами ........................................................................ |
8 |
1.1.6. Задачи вычислений ................................................................................................................................. |
12 |
1.2. ЗАДАНИЕ .......................................................................................................................................................... |
15 |
1.3. ВАРИАНТЫ ЗАДАНИЙ ....................................................................................................................................... |
16 |
1.4. КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................. |
17 |
2. ВВЕДЕНИЕ В МATHCAD ................................................................................................................................. |
19 |
2.1.1. Интерфейс Mathcad .............................................................................................................................. |
19 |
2.1.2. Главное меню .......................................................................................................................................... |
19 |
2.1.3. Панели инструментов ........................................................................................................................... |
20 |
2.1.4. Построение выражений и их вычисление............................................................................................ |
20 |
2.1.5. Стандартные функции ......................................................................................................................... |
21 |
2.1.6. Функции пользователя........................................................................................................................... |
22 |
2.1.7. Дискретные переменные. Построение таблиц................................................................................... |
23 |
3. ЗАНЯТИЕ 2. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ |
|
УРАВНЕНИЙ(СЛАУ)............................................................................................................................................. |
25 |
3.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ............................................................................................................................ |
25 |
3.1.1. Алгебра матриц. Основные понятия и определения........................................................................... |
25 |
3.1.2. Постановка задачи решения СЛАУ ..................................................................................................... |
28 |
3.1.3. Существование и единственность решения СЛАУ............................................................................ |
28 |
3.1.4. Концепция точных методов решения СЛАУ ...................................................................................... |
29 |
3.1.5. Метод Гаусса ......................................................................................................................................... |
29 |
3.1.6. Метод LU-разложения.......................................................................................................................... |
31 |
3.1.7. Выбор ведущего элемента для повышения точности........................................................................ |
33 |
3.1.8. Выбор ведущего элемента для уменьшения количества вычислений ............................................... |
34 |
3.1.9. Метод прогонки ..................................................................................................................................... |
36 |
3.1.10. Метод квадратного корня .................................................................................................................. |
37 |
3.1.11. Решение СЛАУ в MathCad и операции с матрицами ....................................................................... |
38 |
3.2. ЗАДАНИЕ НА РАБОТУ ....................................................................................................................................... |
40 |
3.3. ВАРИАНТЫ ЗАДАНИЙ ....................................................................................................................................... |
40 |
3.4. КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................. |
42 |
4. ЗАНЯТИЕ 3. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ |
|
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ................................................................................................................... |
43 |
4.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ............................................................................................................................ |
43 |
4.1.1. Концепция итерационных методов решения СЛАУ........................................................................... |
43 |
4.1.2. Метод простых итераций.................................................................................................................... |
43 |
4.1.3. Метод Гаусса-Зейделя........................................................................................................................... |
46 |
4.1.4. Проверка сходимости на каждом шаге .............................................................................................. |
47 |
4.2. ЗАДАНИЕ НА РАБОТУ ....................................................................................................................................... |
47 |
4.3. ВАРИАНТЫ ЗАДАНИЙ ....................................................................................................................................... |
47 |
4.4. КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................. |
48 |
5. ЗАНЯТИЕ 4. АЛГЕБРАИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ.............................................................................. |
49 |
5.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ............................................................................................................................ |
49 |
5.1.1. Постановка задачи интерполяции ....................................................................................................... |
49 |
5.1.2. Интерполирование по Вандермонду .................................................................................................... |
50 |
5.1.3. Интерполирование по Лагранжу ......................................................................................................... |
51 |
5.1.4. Интерполяционный полином Ньютона с разделенными разностями .............................................. |
52 |
5.1.5. Интерполяционный полином Ньютона с конечными разностями.................................................... |
52 |
5.1.6. Построение плоского графика функции в MathCad ........................................................................... |
53 |
3
5.2. ЗАДАНИЕ .......................................................................................................................................................... |
56 |
5.3. ВАРИАНТЫ ЗАДАНИЙ ....................................................................................................................................... |
56 |
5.4. КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................. |
57 |
6. ЗАНЯТИЕ 5. ИНТЕРПОЛИРОВАНИЕ СПЛАЙНАМИ .............................................................................. |
58 |
6.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ............................................................................................................................ |
58 |
6.1.1. Построение интерполяционного кубического сплайна ...................................................................... |
58 |
6.1.2. Интерполяция сплайнами в MathCad ................................................................................................... |
59 |
6.2. ЗАДАНИЕ .......................................................................................................................................................... |
59 |
6.3. ВАРИАНТЫ ЗАДАНИЙ ....................................................................................................................................... |
59 |
6.4. КОНТРОЛЬНЫЕ ВОПРОСЫ................................................................................................................................. |
60 |
7. ЗАНЯТИЕ 6. СРЕДНЕКВАДРАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ ФУНКЦИЙ......................................... |
61 |
7.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ............................................................................................................................ |
61 |
7.1.1. Постановка задачи среднеквадратического приближения............................................................... |
61 |
7.1.2. Метод наименьших квадратов............................................................................................................. |
61 |
7.1.3. Среднеквадратическое приближение многочленами ......................................................................... |
62 |
7.1.4. Система многочленов, ортогональных на равномерной сетке......................................................... |
63 |
7.1.5. Работа с файлами в MathCAD ............................................................................................................. |
64 |
7.1.6. Среднеквадратическое приближение полиномами произвольной степени в MathCAD.................. |
66 |
7.2. ЗАДАНИЕ .......................................................................................................................................................... |
67 |
8. ЗАНЯТИЕ 7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ...................................................................................... |
68 |
8.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ............................................................................................................................ |
68 |
8.1.1. Постановка задачи численного интегрирования ................................................................................ |
68 |
8.1.2. Концепция численного интегрирования ............................................................................................... |
68 |
8.1.3. Квадратурные формулы для сетки с равноотстоящими узлами. Квадратурные формулы |
|
Ньютона-Котеса............................................................................................................................................. |
68 |
8.1.4. Частные случаи квадратурных формул Ньютона-Котеса. Простые формулы прямоугольников, |
|
трапеций и парабол (Симпсона)..................................................................................................................... |
69 |
8.1.5. Составные квадратурные формулы численного интегрирования.................................................... |
71 |
8.1.6. Оценка погрешности численного интегрирования ............................................................................. |
72 |
8.1.7. Квадратурные формулы наивысшей алгебраической степени точности ....................................... |
73 |
8.2. ЗАДАНИЕ .......................................................................................................................................................... |
75 |
8.3. ВАРИАНТЫ ЗАДАНИЙ ....................................................................................................................................... |
76 |
4

1. ЗАНЯТИЕ 1. ПРИБЛИЖЕННЫЕ ЧИСЛА И ИХ ПОГРЕШНОСТИ
1.1.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1.1.Виды погрешностей
Различают два вида погрешностей - абсолютную и относительную.
Пусть A и a - два близких числа. Для определенности будем считать, что A - точное число, а a - приближенное.
Абсолютная погрешность приближенного числа a равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:
|
|
|
|
|
|
|||
a |
|
A a |
|
|
|
|||
Относительная погрешность приближенного числа - это отношение абсолютной |
||||||||
погрешности к его модулю: |
|
|
||||||
|
|
|
или в процентах |
|
100% |
|||
| a | |
| a | |
|||||||
|
|
|
|
|||||
Предельная абсолютная погрешность а является верхней оценкой модуля абсолютной погрешности, т. е. | a| a. В дальнейшем значение a принимается в качестве абсолютной погрешности приближенного числа а. В этом случае истинное значение х находится в интервале (а - a, а + a).
Для приближенного числа, полученного в результате округления, предельная абсолютная погрешность a принимается равной половине единицы последнего разряда числа. Например, значение а=0.734 могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом a 0.0005, и полагаем a=0.0005.
Примеры оценки абсолютной погрешности при некоторых значениях приближенной величины а.
а |
51,7 |
-0,0031 |
16 |
16,00 |
|
|
|
|
|
a |
0,05 |
0,00005 |
0,5 |
0,005 |
|
|
|
|
|
При вычислениях на ЭВМ округления, как правило, не производятся, а цифры, выходящие за разрядную сетку машины, отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления.
Предельное значение относительной погрешности: отношение предельной абсолютной погрешности к абсолютной величине приближенного числа:
à à / à
5
1.1.2. Верные и сомнительные значащие цифры приближенного числа
Важной характеристикой приближенного числа является количество его верных значащих цифр.
Значащими цифрами числа в его позиционной записи называются все его цифры, начиная с первой ненулевой слева.
Значащую цифру приближенного числа называют верной, если абсолютная погрешность числа не превосходит половины единицы разряда, в котором стоит эта цифра. Все остальные цифры будут сомнительными.
Для конечных результатов расчѐтов существуют две формы записи: гарантированная – со всеми верными цифрами и форма Крылова – с одной сомнительной цифрой, но погрешность числа при этом не должна превышать 2-х
единиц в разряде сомнительной |
цифры. Предельные |
погрешности в |
5 единиц |
для |
|||
гарантированной |
формы |
и в |
2 единицы |
для |
формы Крылова |
обычно |
не |
указываются. |
|
|
|
|
|
|
|
аг = 4,50 0,004; |
|
dk = 4,50 0,001; |
|
|
|||
bг = 27; |
|
|
ek = 27; |
|
|
|
|
с = 4,03 104; |
|
g |
= 4,03 104 . |
|
|
||
г |
|
|
k |
|
|
|
|
Предельные абсолютные погрешности приведѐнных чисел будут: |
|
|
|||||
а = 0,004; |
b = 0,5; |
c = 0,005 104; |
|
|
|
|
|
d = 0,001; |
e = 2; |
g = 0,02 104 . |
|
|
|
|
|
Предельные погрешности конечных результатов необходимо |
записывать |
в |
|||||
одном разряде. |
|
|
|
|
|
|
|
Приближѐнные числа промежуточных результатов рекомендуется записывать с одной или с двумя сомнительными цифрами и предельными погрешностями в разрядах сомнительных цифр числа.
Пример 1.1. Записать приближѐнное число b = 23,746 0,003 в гарантированной форме и в форме Крылова.
Решение. Цифры числа 2, 3, 7, 4 могут быть верными ; цифра 6 стоит в разряде тысячных и является сомнительной, т . к .
b = 0,003 > 0,0005. |
Произведѐм первое округление до четырѐх значащих цифр числа |
||||
: |
|
|
|
|
|
b |
23,75 ( b bî êð ) 23,75 |
(0,003 | 23,746 – 23,75|) = 23,75 |
0,007 |
|
|
|
Новое число |
имеет сомнительную цифру 5 в разряде сотых, |
т. к. |
||
b |
0,007 0,005 . |
Произведѐм |
новое округление исходного |
числа до |
трѐх |
значащих цифр числа:
b 23,7 ( b bî êð ) 23,7 (0,003 | 23,746 – 23,7|) 23,7 0,049
Замечание. Последовательные округления приближѐнных чисел производить только от
первоначального |
значения числа, чтобы не огрублять последующие результаты. |
|
Новое число |
имеет все цифры верными, т. к. b 0,049 0,05 . Гарантированная |
|
форма заданного приближѐнного числа будет: |
bг = 23,7 . |
|
6
В форме Крылова |
число получаем после первого округления. Действительно |
|
b = 0,007 < 0,02. Исходное число в форме Крылова будет иметь |
вид: bк = 23,75 |
|
0,01. |
|
|
Ответ : bг = 23,7 ; |
bк = 23,75 0,01. |
|
1.1.3. Связь между количеством верных цифр и относительной погрешностью числа
Теорема 1.1. Если приближѐнное число имеет n верных цифр, то его
относительная погрешность не превышает 5 10-n |
|
|
|
|
||||||
Доказательство . Пусть имеем |
приближѐнное |
число |
а с n |
верными цифрами. |
||||||
Запишем его в ―нормализованном‖ виде: |
|
|
|
|
|
|||||
a 0,a a a ...a ×10 p |
где – первая |
цифра |
числа, |
отличная от |
нуля, 0,1 0 |
|||||
1 |
2 |
3 |
n |
1 |
|
|
|
|
|
|
, a1a2 a3 ...an < |
1 |
– |
мантисса |
числа, |
Р – |
показатель степени |
(может |
быть как |
||
положительным, так и отрицательным), называемый порядком числа.
В соответствием с определением верной цифры приближѐнного числа абсолютная погрешность числа а будет:
à 0.000...05 10p 0,5 10 n 10p
n öèô ð
По определению относительная погрешность приближѐнного числа а будет :
|
|
|
|
|
|
a |
|
0.5 10 n |
10p |
|
|
|
|
|
|
|
|
|||||||
a |
|
| a | |
0,a a a ...a |
10p |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 3 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
Для оценки верхней границы относительной погрешности |
приближѐнного числа |
а |
||||||||||||||||||||||
рассмотрим нижнее предельное значение мантиссы числа |
|
|
|
|||||||||||||||||||||
a |
|
|
|
|
0.5 10 n |
|
|
0.5 10 n |
, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 ,a1a2 a3 ...an |
|
|
0.1 |
|
|
|
|
|
|
|
|
|
||||||||
из чего следует a |
5 10 n |
, |
что и требовалось доказать. |
|
|
|||||||||||||||||||
Пример 1.2. |
Определить |
относительную |
погрешность |
чисел |
а = 36,2 0,01 |
и |
||||||||||||||||||
bг = 10 |
|
и сравнить с предельной относительной погрешностью согласно теореме 1.1. |
||||||||||||||||||||||
Решение. |
Число |
|
а |
имеет |
три |
верные |
цифры ( n=3 ). |
Его относительная |
||||||||||||||||
погрешность : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
0.01 |
= 0,00028 |
< 5 10-3 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
а |
|
|
36.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Число b имеет две верные цифры. |
Его относительная погрешность |
|
||||||||||||||||||||||
|
|
|
= |
|
0.5 |
= |
0,05 ( не превышает 5 10-2 ). |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
b |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: а = 0,00028; |
b = 0,05. |
|
|
|
|
|
|
|||||||||||||||||
Обратная теорема 1.2. Если относительная погрешность приближѐнного числа не превосходит 0.5 10-n , то такое число имеет не менее n верных цифр.
Доказательство. В соответствии с определением относительной погрешности
7

абсолютная погрешность приближѐнного числа через его относительную погрешность рассчитывается по формуле : а = a а .
При ―нормализованной форме‖ записи числа с учѐтом условий теоремы имеем:
a = 0,a a a |
...a 10 p0.5 10-n 0.5 10 p-n . |
1 2 3 |
n |
Последнее означает, что приближѐнное число а имеет не менее, чем n верных |
|
цифр (при самом неблагоприятном случае, когда мантисса числа близка к единице), так как его абсолютная погрешность не превосходит 5 единиц в разряде, следующем за n – n-ой цифрой числа а, что и требовалось доказать.
Если мантисса числа будет равна 0,1 (второй крайний случай), то в приближѐнном числе а будет n+1 верная цифра:
aã 0. 100...0 10p
n 1 öèô ðà
Пример 1.3. Определить количество верных цифр n в числе а=9,76, если его относительная погрешность а = 0,5 10-3 .
Решение. Вычислим абсолютную погрешность числа:
а = 9,76 0,5 10-3 = 0,0049 < 0,005
и это означает, что число а имеет три верные цифры. Ответ: n=3 .
1.1.4. Погрешности при вычислении значений функций
Рассмотрим функцию одной переменной y=f(x). Пусть а - приближенное значение аргумента х=a, а — его абсолютная погрешность. Абсолютную погрешность функции можно считать ее приращением, которое можно заменить дифференциалом: у dy. Тогда для оценки абсолютной погрешности получим выражение у =|f (a)| a.
Аналогичное выражение можно записать для функции нескольких аргументов. Пусть y f (x1 , x2 ,..., xn ) - некоторая функция нескольких переменных,
a1 , a2 ,..., an - некоторые значения соответствующих переменных x1 , x2 ,..., xn ,
a1 , a2 ,..., an - их абсолютные погрешности.
Тогда можно дать следующую оценку абсолютной погрешности значения функции:
|
n |
y |
|
|
|
|
y(a1 , a2 |
,..., an ) |
|
ai y . |
(1.1) |
||
a |
||||||
|
i 1 |
|
|
|
||
|
i |
|
|
|
Относительная погрешность при этом может быть найдена обычным образом:
y(a1 , a2 ,..., an ) y(a1 , a2 ,..., an ) y. | y(a1 , a2 ,..., an ) |
1.1.5. Погрешности операций над приближенными числами
Абсолютная погрешность суммы небольшого количества (<10) приближенных чисел:
8

|
|
( n ai ) |
|
|
n |
n |
|
n |
|
( ai |
) |
i 1 |
|
ai ai . |
|
|
|
|
|
i 1 |
i 1 |
ai |
|
i 1 |
|
|
|
|
|
Абсолютная погрешность суммы большого количества ( n 10 ) приближенных чисел (правило Чеботарева, полученное на основе теории вероятностей):
s a 
 n ; a = max ai
n ; a = max ai
Относительная погрешность разности
(a b) a b,
Относительная погрешность суммы
(a b) a b
| a b |
Она лежит между относительными погрешностями слагаемых, поэтому ее обычно принимают равной максимальной из них: (a b) max( a , b ) .
Относительная погрешность разности двух приближенных чисел:
(a b) |
(a b) |
|
a b . |
|
| a b | |
|
| a b | |
Относительная погрешность умножения или деления приближенных чисел:
|
|
n |
|
n |
|
n |
m |
|
n |
m |
|
|
|
ai |
ai |
, |
ai |
/ bj |
ai |
bj . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
i 1 |
i 1 |
j 1 |
|
i 1 |
j 1 |
||||
|
Относительная погрешность при умножении или делении большого количества |
||||||||||
приближенных чисел: |
|
|
|
|
|
|
|||||
При |
m n 10 по правилу Чеботарѐва: |
|
|||||||||
|
|
|
|
|
|
|
|||||
v |
c |
n m , c max( ai , bj ) |
|
|
|
||||||
|
|
|
|
|
|
i, j |
|
|
|
|
|
|
Абсолютная погрешность умножения приближенного числа на точное число k : |
||||||||||
(ak) k a , |
|
|
|
|
|
|
|
|
|||
|
Относительная погрешность умножения на точное число k : |
||||||||||
|
(ak) a a/ | a | . |
|
|
|
|
|
|||||
|
Относительная погрешность возведения в степень: |
||||||||||
|
(ak ) k a. |
|
|
|
|
|
|
||||
|
Пример 1.4. Вычислить сумму и определить еѐ погрешность: |
||||||||||
|
|
|
|
a1= 117,89 |
|
|
a1= 0,003 |
||||
9
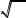
a2= 11,671 |
a2= 0,0002 |
a3= 0,34 |
a3= 0,004 |
a4= 0,0576 |
a4= 0,0001 |
Решение.
S=129,9586 ; S a1+ a3 = 0,007.
Результат в форме Крылова: Sк= 129,96 0,01;
Гарантированный результат: Sг= 130,0 .
Если в результате алгебраического сложения модуль результата оказывается близким к нулю, то происходит потеря знаков, что приводит к резкому возрастанию относительной погрешности результата.
Пример 1.5. Вычислить сумму S= 14,3 + 5,4 + 0,3 (слагаемые записаны с верными цифрами), сравнить относительную погрешность суммы с относительными погрешностями слагаемых.
Решение. S = 20; абсолютная погрешность суммы
s = 0,05 + 0,05 + 0,05 = 0,15;
относительная погрешность суммы s = s/s = 0,15/20 = 0,0075; вычислим относительные погрешности слагаемых:
1 = 0,05/14,3 = 0,0035; 2 = 0,05/5,4 = 0,0093; 3 = 0,05/0,3 = 0,17.
Легко заметить, что относительная погрешность суммы находится между
погрешностями наиболее точного и наиболее неточного слагаемых : |
0,0035 < s < 0,17. |
|||
Ответ: s = 20; |
s = 0,15. |
|
|
|
Пример 1.6. |
|
|
|
|
Вычислить результат и определить его погрешность: |
|
|
||
S ai , где |
|
|
|
|
à1 12,34; à2 |
0,481; à3 2,376; à4 |
0,0734; à5 111,642; à6 |
9,4314; |
|
à7 0,2936; à8 |
0,1122; à9 98,364; |
à10 = 0,0343;à11 |
0,982; à12 = 17,553; |
|
Все слагаемые даны в гарантированной форме записи. |
|
|
||
Решение. |
|
|
|
|
Число слагаемых больше 10 (n = 12) . Алгебраическая |
сумма |
|
||
s = 19,5959 .
Для отыскания погрешности суммы применим правило Чеботарѐва |
|
(n = 12 > 10) |
|
max ai = a1 = 0,005; |
s = 0,005 12 = 0,018. |
Ответ: s = 19,6 0,02.
Пример 1.7. Вычислить дробь
10
