
MU_LR_VychMat_230400
.pdf
может состоять из латинских, русских, греческих и других букв и цифр, знаков подчеркивания (_), штриха (`), символа процента (%), , вводимых с клавиатуры.
Имена переменных и функций не могут начинаться с цифры, знака подчеркивания, штриха, символа процента (%), не могут включать в себя пробелы. Символ бесконечности может быть только первым символом в имени.
Mathcad воспринимает заглавные и строчные буквы как различные идентификаторы, то же касается букв, изображенных различными шрифтами — это разные имена.
Mathcad не делает различий между именами переменных и функций. Если определить вначале функцию f(x), а затем переменную f, окажется невозможным использовать f(x) в последующих расчетах где-либо ниже определения f.
Mathcad 12 не допускает переопределения значений функций. Mathcad 13 и 14 разрешают, но предупреждают о нем появлением волнистой линии под именем функции. В окне Preferance (рис. 2), выбрав вкладку Warnings, можно такие предупреждения отключить.
Некоторые имена уже используются Mathcad для встроенных констант, единиц измерения, функций. Имена можно переопределить, но имейте в виду, что это уничтожит их встроенные значения и этими константами, функциями пользоваться будет нельзя.
Оператор присваивания (:=) может быть выбран на математической панели Calculator (Калькулятор_____). Познакомьтесь с содержанием панели. При наведении стрелки указателя мыши на какую-либо кнопку появляется всплывающая подсказка с названием оператора, вызываемого при щелчке на этой кнопке, и указанием клавиши или сочетания клавиш, нажатие которых вызывает то же действие, что и щелчок на кнопке. Оператор присваивания также можно ввести с клавиатуры, нажав клавишу «двоеточие»
(:).
Все операции в Mathcad продублированы. Их можно ввести:выбрав соответствующий пункт меню;
нажав соответствующую клавишу (сочетание клавиш) на клавиатуре.
Набрав вычисляемое выражение, нажмите клавишу (=) — появится численный результат (рис 3).
Попробуйте набрать +4xy — у вас получилось 4yx+. Для правильной записи надо нажать клавишу пробел, чтобы уголок курсора охватывал нужную часть выражения (в нашем случае x+). Другой способ — взять в скобки выражение ()x+. В некоторых случаях это просто необходимо.
Рис. 3 - Пример построения математических выражений
2.1.5. Стандартные функции
Mathcad содержит свыше 200 встроенных функций. На стандартной панели нажмите
21

кнопку f(x). Вы увидите список всех встроенных функций. Просмотрите группы функций (левый список). Щелкнув мышью на любой из групп функций слева, вы увидите справа перечень функций, входящих в эту группу.
Названия функций можно вводить со стандартной панели из раскрытого окна функций f(x), выделив название функции и нажав кнопку Insert (Вставить), или набрав имя функции на клавиатуре в точности так, как оно записано в окне функций. Примеры использования некоторых функций приведены на рис. 4.
Рис. 4 - Примеры использования встроенных констант и функций
2.1.6. Функции пользователя
Удобство и эффективность расчетов в Mathcad прежде всего определяется возможностью и легкостью создания функций пользователя. При многократном использовании одного и того же выражения без функций пользователя просто не обойтись.
Вид функции пользователя:
слева название функции (с параметрами в скобках), справа, после оператора присваивания :=, вычисляемое выражение (рис. 5).
Переменные величины, входящие в правую часть, должны быть записаны в параметры после имени функции. Все величины из правой части, не входящие в параметры левой части, должны быть заданы численно левее и выше функции пользователя. В противном случае Mathcad указывает на ошибку, окрашивая незаданную величину в красный цвет. При выделении функции щелчком мыши появляется текст сообщения об ошибке This variable is not definited above (Эта переменная не определена ранее).
Функция пользователя не вычисляется Mathcad, а принимается к сведению. Для вычисления функции надо задать численные значения всех параметров в имени функции, набрать имя функции и нажать клавишу = или щелкнуть мышью по кнопке = на стандартной панели Mathcad, либо в математическом меню на панели Calculator Toolbar (Калькулятор).
22

Рис. 5 - Функции пользователя
2.1.7. Дискретные переменные. Построение таблиц
Одно из лучших творений создателей Mathcad — это дискретная переменная, выполняющая роль оператора цикла. В ряде книг по Mathcad ее называют ранжированная переменная. Это не лучший перевод выражения range variable. Выражение дискретная переменная, использовавшееся в ранних книгах, более точно отражает суть понятия — диапазон изменения переменной: вместо непрерывной переменной используется ряд чисел, выстроенных в порядке возрастания или убывания. Простота использования этого оператора восхищает. Без использования дискретной переменной было бы очень сложно построить графики, вывести таблицы результатов расчета. Если в функцию пользователя подставить численное значение переменной, результатом расчета будет число. Дискретная переменная задает ряд значений переменной, для которых вычисляется функция пользователя. Этот ряд значений функции можно вывести в виде графика или таблицы.
Ответ выводится в виде вектора — столбца чисел (рис. 6) — или графика.
Рис. 6 - Дискретные переменные. Числовые результаты выведены для функций, приведенных на рис. 5
Дискретная переменная может задавать как целые, так и дробные значения переменной, но обязательно равноотстоящие друг от друга, например:
23

рассматриваются разные варианты одного расчета и изменение констант и AB позволяет мгновенно пересчитать результаты и перестроить графики.
Две точки – знак диапазона нельзя набирать с клавиатуры, нажимая два раза клавишу «точка». Надо на клавиатуре нажать клавишу ; (точка с запятой) или в математической панели выбрать Matrix (значок матрицы) 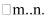
24

3. ЗАНЯТИЕ 2. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ(СЛАУ)
3.1.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
3.1.1.Алгебра матриц. Основные понятия и определения
Система тп чисел (действительных или комплексных), расположенных в прямоугольной таблице из т строк и п столбцов,
|
а11 |
|
а12 |
а13 |
|
|
а1п |
|
|
|
|
А = |
|
а |
|
а |
а |
|
|
а |
|
|
, |
|
21 |
|
22 |
23 |
|
|
2 п |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
а |
а |
|
|
а |
|
|
|
|
|
т1 |
|
т2 |
т3 |
|
|
тп |
|
|
|
называется матрицей (числовой).
Числа аij ( i = 1,2, , т; j = 1,2, , п), составляющие данную матрицу, называются еѐ элементами.
Равенство матриц
Две матрицы А = [aij] и B = [bij] считаются равными: А=В, если они одного и того же типа, т.е. имеют одинаковое число строк и столбцов, и соответствующие элементы их равны, т.е.
aij = bij.
Сумма и разность матриц
Суммой двух матриц A = [aij] и B = [bij] одинакового типа называется матрица C = [cij]того же типа, элементы которой cij равны суммам соответствующих элементов aij и bij матриц А и В, т.е. сij = aij + bij. Таким образом,
а11 |
b11 |
|
a12 |
|
b12 |
|
|
|
|
a1n |
b1n |
|
|
|||
|
а |
21 |
b |
|
a |
|
b |
|
|
|
|
a |
b |
|
|
|
A B |
|
21 |
|
22 |
|
22 |
|
|
|
|
2n |
2n |
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
b |
|
a b |
|
|
|
|
a b |
|
||||||
|
|
m1 |
m1 |
m2 |
m2 |
|
|
|
mn |
|
|
|
||||
|
|
|
|
|
mn |
|||||||||||
Из определения суммы матриц непосредственно вытекает следующие еѐ свойства:
1)А + (В + С) = (А + В)+С;
2)А + В + В + А;
3)А + 0 = А.
Умножение матриц Пусть
|
а11 |
а12 |
а1п |
|
|
b11 |
b12 |
b1q |
|
|||||
А = |
|
а |
а |
а |
|
, |
b |
|
b |
|
b |
|
|
|
|
21 |
22 |
2 п |
|
В = |
21 |
22 |
2 q |
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
а |
а |
а |
|
|
b |
p1 |
b |
p 2 |
b |
|
|
|
|
|
т1 |
т2 |
тп |
|
|
|
|
|
pq |
||||
- матрицы типов соответственно т п и p q. Если число столбцов матрицы А равно
25

числу строк матрицы В, т.е. п = р, то для этих матриц определена матрица С типа m q,
называемая их произведением:
|
с11 |
с12 |
с1q |
|
|
|
|
с |
с |
с |
|
|
|
С = |
21 |
22 |
2 q , |
|
|
|
|
|
|
|
|||
|
с |
с |
с |
|
|
|
|
m1 |
m2 |
mq |
|
|
|
где cij |
ai1bij |
ai 2b2 j |
... aimbmj |
(i 1,2,...,m; j |
1,2,..,q) . |
|
Из определения вытекает следующее правило умножения матриц: чтобы получить элемент , стоящий в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-й строки первой матрицы умножить на соответствующие элементы j-го столбца второй и полученные произведения сложить.
Произведения АВ имеет смысл тогда и только тогда, когда матрица А содержит в строках столько элементов, сколько элементов имеется в столбцах матрицы В. В частности, можно перемножать квадратные матрицы лишь одинакового порядка.
Транспонированная матрица Заменив в матрице типа п т
а11 |
а12 |
а1п |
|
|
||
а |
|
а |
а |
|
, |
|
А |
|
21 |
22 |
2п |
|
|
|
|
|
|
|||
а |
т1 |
а |
а |
|
|
|
|
|
т2 |
тп |
|
||
строки соответственно столбцами, получим так называемую транспонированную матрицу
|
а11 |
а21 |
ат1 |
|
|
|
Т |
а |
а |
а |
|
, |
|
А А |
|
12 |
22 |
т2 |
|
|
|
|
|
|
|
||
|
а |
а |
а |
|
|
|
|
|
1п |
2п |
тп |
|
|
Обратная матрица Обратной матрицей по отношению к данной называется матрица, которая, будучи
умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. Для матрицы А обозначим ей матрицу через А-1. Тогда по определению имеем:
АА 1 А 1 А Е
где Е – единичная матрица.
Нахождение обратной матрицы для данной называется обращением данной матрицы.
Ранг матрицы Пусть дана прямоугольная матрица
|
a11 |
|
a12 |
|
a1n |
|
|
|
|
|
a22 |
|
|
a2n |
|
A |
a21 |
|
|
|
|||
|
|
|
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
am1 |
|
am2 |
|
amn |
||
Если в этой матрице выбрать произвольным образом k строк и k столбцов, где
26

k min m, n , то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу порядка k. Определитель этой матрицы называется минором k-го порядка матрицы А.
Определение. Рангом матрицы называется максимальный порядок отличного от нуля минора матрицы.
Иными словами, матрица А имеет ранг r, если:
1)найдется по меньшей мере один еѐ минор r-го порядка, отличный от нуля;
2)все миноры матрицы А порядка r+1 и выше равен нулю.
Следствие.
Ранг матрицы равен минимуму из количества ее линейно независимых строк и количества ее линейно независимых столбцов.
Ранг нулевой матрицы т.е. матрицы, состоящей из нулей, считается равным нулю. Разность между наименьшим из чисел т и п и рангом матрицы называется дефектом матрицы. Если дефект равен нулю, то ранг матрицы – наибольший из возможных для ее типа.
Треугольные матрицы Квадратная матрица называется треугольной, если элементы, стоящие выше (ниже)
главной диагонали, равны нулю. Например,
t11 |
|
t12 |
|
|
|
|
t1n |
|
|
||||
|
0 |
|
|
t |
|
|
|
|
|
t |
|
|
, |
Ò |
|
|
|
|
22 |
|
|
|
|
|
2n |
||
|
|
|
|
|
|||||||||
|
0 |
|
|
|
0 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
|
где tij = 0 при i > j,есть верхняя треугольная матрица.
Нормы матрицы |
|
|
|
|
|
||||||
Нормой |
|
матрицы |
A {ai, j } |
(i, j 1,..., n) называется действительное число |
|||||||
(обозначаемое |
|
A |
|
), удовлетворяющее условиям: |
|||||||
|
|
||||||||||
1) |
|
0 |
при A 0 и |
|
A |
|
0 тогда и только тогда, когда A - нулевая матрица; |
||||
A |
|
|
|||||||||
2)
 A
A


 A
A
 для любого действительного ;
для любого действительного ;
3)
 A1 A2
A1 A2 


 A1
A1 


 A2
A2 
 , где A1 , A2 - некоторые матрицы;
, где A1 , A2 - некоторые матрицы;
4)
 A1 A2
A1 A2 


 A1
A1 


 A2
A2 
 , где A1 , A2 - матрицы, для которых соответствующие операции имеют смысл.
, где A1 , A2 - матрицы, для которых соответствующие операции имеют смысл.
Наиболее употребительными являются следующие нормы матриц и векторов, образованных действительными компонентами.
Нормы матрицы A |
Нормы вектора x |
|||||||||||
|
|
|
|
n |
|
|
|
|
|
|
||
1) |
A |
1 |
max |
ai, j |
; |
1) |
x |
1 |
max |
xi |
; |
|
|
|
|
i |
j 1 |
|
|
|
i |
||||
|
|
|
|
|
|
|
|
|
|
|||
27

|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||||
2) |
|
A |
|
|
|
|
|
2 max |
ai, j |
; |
2) |
|
|
x |
|
|
|
|
|
|
2 |
|
xi |
|
; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
j |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||||
3) |
|
A |
|
|
|
3 |
aij2 ; |
3) |
|
|
x |
|
|
|
3 |
xi2 . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
||||||||
3.1.2. Постановка задачи решения СЛАУ
Пусть дана система линейных алгебраических уравнений
|
|
|
|
|
|
|
AX B , |
(2.1) |
|
|
a1,1 |
... |
a1,n |
|
|
|
|
где A ... |
|
... ... |
|
- матрица коэффициентов при неизвестных [n n], |
|
|||
|
|
|
|
|
|
|
|
|
|
|
an,1 |
... |
an,n |
|
|
||
b [b ,...,b ]T |
- вектор-столбец свободных членов [n 1] , |
|
||||||
|
1 |
n |
|
|
|
|
|
|
x [x ,..., x ]T |
- вектор-столбец неизвестных [n 1] . |
|
||||||
|
1 |
n |
|
|
|
|
|
|
В развернутой форме система (2.1) имеет вид: |
|
|||||||
a11 x1 |
a12 x2 |
... a1n xn |
b1 , |
|
||||
a |
x |
a |
x |
... a |
x |
b , |
|
|
21 |
1 |
22 |
2 |
... |
2n |
n |
2 |
|
|
|
|
|
|
|
|
|
|
x |
a |
x |
... a |
x |
b . |
|
||
a |
|
|||||||
n1 |
1 |
n2 |
2 |
|
nn |
n |
n |
|
Требуется найти такой вектор x* [x1* ,..., xn* ]T , который при подстановке в систему (2.1), превращает ее в тождество.
3.1.3. Существование и единственность решения СЛАУ
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной (противоречивой), если она не имеет решений. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если более одного решения.
Теорема Кронекера-Капелли.
СЛАУ (2.1) тогда и только тогда совместна, когда ранг расширенной матрицы A ( A | B) , образованной присоединением к матрице A вектора свободных членов B , равен рангу матрицы A .
Совместная СЛАУ вида (2.1) имеет единственное решение тогда и только тогда, когда ранг матрицы A равен числу неизвестных: r(A) n .
Если r(A) n , то СЛАУ имеет бесконечное множество решений.
Следствие:
Решение СЛАУ (2.1) существует и единственно тогда и только тогда, когда det( A) 0 .
28
Примеры:
|
2 |
3 |
5 x1 |
|
1 |
|
|
|
1) |
1 |
4 |
1 x |
|
2 |
r(A) r( |
A |
) n 3 => система является определенной (имеет |
|
|
2 |
2 |
|
|
|
|
|
|
3 |
6 x3 |
3 |
|
|
|
||
единственное решение)
|
1 |
0.5 |
5 x1 |
|
1 |
r(A) 2 r( |
|
) 3 => система не совместна (не |
|
2) |
2 |
1 |
10 |
x2 |
|
2 |
A |
||
|
|
2 |
6 |
|
|
|
|
|
|
|
3 |
x3 |
|
3 |
|
|
|
||
имеет решений)
|
1 |
0.5 |
5 x1 |
|
|
3 |
r(A) r( |
|
) 2 (n 3) => система является |
|
3) |
2 |
1 |
10 |
x2 |
|
6 |
A |
|||
|
|
2 |
6 |
|
|
|
|
|
|
|
|
3 |
x3 |
|
|
3 |
|
|
|
||
совместной, но не определенной (имеет бесконечное множество решений)
|
2 |
3 |
0 x1 |
|
1 |
r(A) 2 r( |
|
) 3 => система не совместна (не имеет |
4) |
1 |
4 |
0 x2 |
|
2 |
A |
||
|
|
2 |
|
|
|
|
|
|
|
3 |
0 x3 |
|
3 |
|
|
|
решений)
3.1.4. Концепция точных методов решения СЛАУ
Точные (прямые) методы позволяют найти точные решение системы после конечного числа арифметических операций, каждая из которых выполняется точно, т.е. в предположении отсутствия округлений.
3.1.5. Метод Гаусса
Метод Гаусса состоит в последовательном исключении неизвестных путем осуществления эквивалентных преобразований системы, не изменяющих ее решение, и реализуется в два этапа, называемых, соответственно, прямым и обратным ходом.
Прямой ход состоит в преобразовании исходной системы к эквивалентному виду с верхней треугольной матрицей коэффициентов при неизвестных и единичной диагональю.
Введем обозначения: ai(0), j ai, j ,i, j 1,...,n и an(0)1, j bj , j 1,..., n .
Для системы из n уравнений с n неизвестными прямой ход осуществляется за n шагов и схематически может быть представлен в виде:
a(0) |
a(0) |
... |
a(0) |
a(0) |
|
1 |
a(1) |
... |
a(1) |
a(1) |
|
1 |
|||
|
11 |
12 |
|
1n |
1,n 1 |
|
|
|
12 |
|
1n |
1,n 1 |
|
|
|
a(0) |
a(0) |
... |
a(0) |
a(0) |
|
|
0 |
a(1) |
... |
a(1) |
a(1) |
|
|
0 |
|
|
21 |
22 |
|
2n |
2,n 1 |
|
|
|
22 |
|
2n |
2,n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
... ... ... |
... |
|
... ... |
... ... |
... |
|
... ... |
||||||
a(0) |
a(0) |
... |
a(0) |
a(0) |
|
|
0 |
a(1) |
... |
a(1) |
a(1) |
|
|
0 |
|
|
n1 |
n2 |
|
nn |
n,n 1 |
|
|
|
n2 |
|
nn |
n,n 1 |
|
|
|
Общие формулы прямого хода метода Гаусса имеют вид:
a(k ) a(k 1) |
/ a(k 1) |
|
|
|
kj |
kj |
kk |
|
|
a(k ) a(k 1) |
a(k 1) |
a(k ) ; |
|
|
ij |
ij |
ik |
kj |
|
k 1, |
2,..., |
n; i k 1,..., n; |
j k 1,..., n 1 |
|
a(1) |
... |
a(1) |
a(1) |
|
12 |
|
1n |
1,n 1 |
|
1 |
... |
a(2) |
a(2) |
|
|
|
2n |
2,n 1 |
|
... ... ... |
... |
|
||
|
|
|
(n) |
|
0 |
... |
1 |
an,n 1 |
|
(2.2)
29

В результате система уравнений приводится к виду:
x1 a12( 1 ) x2 a13( 1 ) x3 ... a1(n1 ) xn a1(,n1 ) 1 x2 a23( 2 ) x3 ... a2( n2 ) xn a2( ,n2 ) 1
...................... (2.3)
x |
x a(n 1) |
a(n) |
n 1 |
n n 1,n 1 |
n,n 1 |
|
x |
a(n) |
|
n |
n,n 1 |
Обратный ход заключается в произведении обратной подстановки для нахождения неизвестных, начиная с последнего. Формулы обратной подстановки имеют вид:
|
n |
|
|
|
xn an,n 1; |
xi ai,n 1 ai, j xj ; |
i n 1, |
n 2,...,1 |
(2.4) |
j i 1
Верхние индексы в (2.4) опущены.
Вычислительная сложность метода Гаусса составляет порядка n3 операций.
Пример решения СЛАУ методом Гаусса Пусть надо решить систему линейных алгебраических уравнений третьего порядка.
2 5 |
3 |
x1 |
3 |
||||
3 |
1 |
6 |
|
x2 |
23 |
||
|
|
|
|
|
|
|
|
1 |
4 |
2 |
|
x3 |
13 |
||
|
|
|
|
|
|
|
|
Проследим изменение элементов расширенной матрицы. Исходная матрица
|
k 0 |
|
I шаг: k=1; j=2, 3, 4; i=2, 3, 4 |
||||||
2 |
5 |
3 |
3 |
|
1 |
5/ 2 |
3/ 2 |
3/ 2 |
|
|
|
||||||||
3 |
1 |
6 |
23 |
|
0 |
13/ 2 |
21/ 2 |
37 / 2 |
|
1 4 |
2 |
13 |
|
0 |
13/ 2 |
1/ 2 |
29 / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
II шаг: k=2; j=3, 4; i=3, 4 |
III шаг: k=3; j=4; i =4 |
|
||||||||
|
3/ 2 |
3/ 2 |
|
1 5/ 2 |
3/ 2 |
3/ 2 |
|
|||
|
1 5/ 2 |
|
|
|||||||
|
0 |
1 |
21/ 13 |
37 / 13 |
|
0 |
1 |
21/ 13 |
37 / 13 |
|
|
0 |
0 |
11 |
33 |
|
0 |
0 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, мы получили систему с верхней треугольной матрицей.
|
3 / 2 |
|
x1 |
|
3 / 2 |
|
|
1 5 / 2 |
|
|
|
||||
0 |
1 |
21 / 13 |
|
x2 |
|
37 / 13 |
|
0 |
0 |
1 |
|
x3 |
|
3 |
|
|
|
|
|
|
|
|
|
Решаем эту систему обратной подстановкой:
х3=3;
х2=-37/13 + 21/13 . х3=2;
х1=3/2- 5/2 х2+3/2. х3= 1.
30
