
MU_LR_VychMat_230400
.pdf
|
|
|
3 |
0,1 |
1 |
|
|
|
|
2 |
|
||||
|
|
0,5 7 |
0, 2 |
|
|
B |
|
1 |
|
|
|||||
3. A |
, |
|
|
|
|||||||||||
|
|
0.4 |
2 |
4 |
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
0.5 |
0, 2 |
2 |
|
|
|
2 |
|
|
|
|||||
|
|
0,3 |
1 |
0, 4 |
|
, |
|
|
1 |
|
|
|
|||
5. A |
|
B |
|
|
|
||||||||||
|
|
|
4 |
2 |
1 |
|
|
|
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
6 |
2 |
1 |
|
|
|
2 |
||||||
|
|
|
1 |
5 |
|
|
|
, |
|
|
1 |
|
|||
7. A |
|
0,5 |
B |
|
|||||||||||
|
|
0, 4 |
0, 2 |
2 |
|
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|||||||||
|
|
|
6 |
0, 2 |
0,5 |
|
|
|
2 |
|
|||||
|
|
0, 4 |
4 |
|
|
|
, |
B |
|
1 |
|
|
|||
9. A |
1,5 |
|
|
|
|||||||||||
|
|
0,1 |
3 |
7 |
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
8 |
2 |
0, 4 |
|
|
2 |
|
|
|
||||
11. |
A |
|
3 |
10 |
0, 2 |
|
, |
|
|
1 |
|
|
|
||
|
|
B |
|
|
|
||||||||||
|
|
|
0.5 |
1 |
6 |
|
|
|
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
10 |
0,5 |
2 |
|
|
|
|
|
2 |
|||||
13. |
A |
|
1 |
7 |
0, 2 |
|
, |
B |
|
1 |
|
||||
|
|
|
|
||||||||||||
|
|
|
0.4 |
0,1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||
|
|
|
6 |
2 |
1 |
|
|
|
2 |
|
|||||
15. |
A |
|
0,3 |
5 |
0, 4 |
|
, |
B |
|
1 |
|
|
|||
|
|
|
|
|
|||||||||||
|
|
|
0.5 |
0, 2 |
7 |
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
10 |
2 |
1 |
|
|
|
2 |
|||||||
17. |
A |
|
1 |
4 |
|
|
|
, |
B |
|
1 |
|
|||
|
0,5 |
|
|
||||||||||||
|
|
|
0, 4 |
0, 2 |
3 |
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 |
0, 2 |
0,5 |
|
|
|
2 |
|
|||||
19. |
A |
|
0, 4 |
8 |
1,5 |
|
, |
B |
|
1 |
|
|
|||
|
|
|
|
|
|||||||||||
|
|
|
0,1 |
2 |
6 |
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
3 |
0,1 |
0, 4 |
|
1 |
|
||||||||
21. |
A |
|
1 |
4 |
|
|
|
|
4 |
|
|
||||
|
0, 2 , |
B |
|
|
|||||||||||
|
|
|
0.5 |
2 |
6 |
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 |
2 |
1 |
|
|
|
1 |
|
|||||
23. |
A |
|
0,3 |
1 |
0, 4 |
|
, |
B |
|
4 |
|
|
|||
|
|
|
|
|
|||||||||||
|
|
|
0.5 |
0, 2 |
2 |
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
6 |
0, 2 |
0,5 |
|
|
|
1 |
||||||
25. |
A |
|
0, 4 |
4 |
1,5 |
|
, |
B |
|
|
|
|
|
||
|
|
|
4 |
||||||||||||
|
|
|
0,1 |
3 |
7 |
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
3 |
0,1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|||
4. |
|
|
0,5 |
|
7 |
|
|
, |
|
|
2 |
|
|
|
|
|
|
||
A |
|
0, 2 |
B |
|
|
|
|
|
|
||||||||||
|
|
|
0.4 |
|
2 |
4 |
|
|
|
|
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0,5 |
0, 2 |
2 |
|
|
|
|
1 |
|
|
|
|
||||||
6. |
|
|
0,3 |
|
1 |
0, 4 |
|
, |
|
|
2 |
|
|
|
|
||||
A |
|
|
B |
|
|
|
|
||||||||||||
|
|
|
|
4 |
2 |
1 |
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
6 |
|
2 |
1 |
|
|
1 |
|
|
|||||||
|
|
|
0, 4 |
0, 2 |
2 |
|
|
, |
|
|
2 |
|
|
|
|
||||
8. A |
|
|
B |
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
5 |
0,5 |
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
6 |
|
0, 2 |
0,5 |
|
|
|
1 |
|
|||||||
10. |
A |
|
0, 4 |
|
4 |
1,5 |
|
, |
B |
|
2 |
|
|
||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
0,1 |
|
3 |
|
7 |
|
|
|
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
8 |
|
2 |
0, 4 |
|
|
1 |
|
|
|
|
|||||
12. |
A |
|
3 |
|
10 |
0, 2 |
|
, |
|
|
2 |
|
|
|
|
||||
|
|
|
B |
|
|
|
|
||||||||||||
|
|
|
|
0.5 |
|
1 |
6 |
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
10 |
|
0,5 |
2 |
|
|
|
|
1 |
|
|
||||||
14. |
A |
|
1 |
|
7 |
0, 2 |
|
, |
B |
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
0.4 |
|
0,1 |
4 |
|
|
|
|
|
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
6 |
|
2 |
|
|
1 |
|
|
|
|
1 |
|||||
16. |
A |
|
0,3 |
5 |
|
|
|
|
|
, B |
|
|
2 |
|
|||||
|
|
0, 4 |
|
|
|
||||||||||||||
|
|
|
|
0.5 |
|
0, 2 |
|
7 |
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
10 |
|
2 |
|
1 |
|
|
|
1 |
|
|||||||
18. |
A |
|
1 |
|
4 |
|
|
|
|
, |
B |
|
2 |
|
|
||||
|
|
0,5 |
|
|
|
||||||||||||||
|
|
|
|
0, 4 |
|
0, 2 |
|
3 |
|
|
|
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
4 |
|
0, 2 |
0,5 |
|
|
|
1 |
||||||||
20. |
A |
|
0, 4 |
|
8 |
1,5 |
|
|
|
|
2 |
|
|||||||
|
|
, B |
|
|
|||||||||||||||
|
|
|
|
0,1 |
2 |
|
|
6 |
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
3 |
|
0,1 |
1 |
|
|
|
1 |
|
|
||||||
22. |
A |
|
0,5 |
|
7 |
|
|
|
, |
B |
|
4 |
|
|
|
||||
|
|
0, 2 |
|
|
|
|
|||||||||||||
|
|
|
|
0.4 |
|
2 |
4 |
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
6 |
|
2 |
1 |
|
|
|
1 |
|
|||||||
24. |
A |
|
1 |
|
5 |
|
|
|
|
, |
B |
|
4 |
|
|
||||
|
|
0,5 |
|
|
|
||||||||||||||
|
|
|
|
0, 4 |
|
0, 2 |
|
2 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
8 |
|
2 |
0, 4 |
|
|
1 |
|
|
|
|
|||||
26. |
A |
|
3 |
|
10 |
0, 2 |
|
, |
|
|
4 |
|
|
|
|
||||
|
|
|
B |
|
|
|
|
||||||||||||
|
|
|
|
0.5 |
|
1 |
6 |
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
41
|
10 0,5 |
2 |
|
|
1 |
|
6 |
2 |
1 |
|
|
1 |
|
|
||||||
27. |
|
1 |
7 |
0, 2 |
|
, |
|
4 |
|
28. |
|
0,3 |
5 |
0, 4 |
|
, |
|
4 |
|
|
A |
|
B |
|
A |
|
B |
|
|
||||||||||||
|
|
0.4 |
0,1 |
4 |
|
|
|
2 |
|
|
|
0.5 |
0, 2 |
7 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
10 |
2 |
1 |
|
|
1 |
|
4 0, 2 |
0,5 |
|
|
1 |
||||||||
29. |
|
1 |
4 |
|
|
, |
|
4 |
|
30. |
|
0, 4 |
8 |
1,5 |
|
, B |
|
4 |
|
|
A |
0,5 |
B |
|
A |
|
|
|
|||||||||||||
|
|
0, 4 |
0, 2 |
3 |
|
|
|
2 |
|
|
|
0,1 |
2 |
6 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3.4.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что называется решением СЛАУ?
2.Каковы условия существования решения СЛАУ?
3.Каковы условия единственности решения СЛАУ?
4.В чем состоит метод Гаусса для решения систем линейных уравнений
5.В чем состоит метод LU-разложения для решения систем линейных уравнений
6.Какова вычислительная сложность метода Гаусса?
7.Какова вычислительная сложность метода LU-разложения ?
8. Какой из методов Вы бы применили при необходимости решать нескольких систем линейных уравнений с одинаковой левой и разными правыми частями?
9. Для каких систем линейных уравнений применяется метод квадратного корня?
42

4. ЗАНЯТИЕ 3. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
4.1.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
4.1.1.Концепция итерационных методов решения СЛАУ
Решения, получаемые с помощью прямых методов, обычно содержат погрешности, вызванные округлением при выполнении операций над числами с плавающей точкой на ЭВМ с ограниченным числом разрядов. В ряде случаев эти погрешности могут быть значительными и необходимо найти способ их уменьшения.
Итерационные методы, в отличие от прямых, основаны на многократном уточнении приближенного заданного решения исходной системы. Они позволяют найти решение с любой требуемой точностью (при условии, что погрешность округлений, по крайней мере, на 1-2 порядка меньше требуемой точности).
4.1.2. Метод простых итераций
Простейшим итерационным методом решения СЛАУ является метод простых
итераций. Его суть сводится к следующему. |
|
|
|
|
1. Исходная задача |
|
|
|
|
AX B |
|
|
|
(3.1) |
приводится к равносильному виду: |
|
|
|
|
x αx β , |
|
|
|
(3.2) |
где α { i, j } - квадратная матрица, β {bi } - вектор, |
i, j 1,..., n . |
|
||
Это преобразование может быть выполнено различными путями, но для обеспечения |
||||
сходимости итерационного процесса надо добиться, чтобы |
|
1. |
|
|
α |
|
|||
2. Вектор β принимается в качестве начального приближения, т.е. |
x(0) β и далее |
|||
многократно выполняются действия по уточнению решения согласно рекуррентному соотношению
|
|
|
|
|
|
|
|
|
x(k 1) |
αx(k ) β , k 0,1, 2,... |
(3.3) |
||||
или в развернутом виде |
|
|
|
|
|
|
|
|
|
|
|||||
|
x(k 1) |
|
|
x(k ) |
x(k ) |
... |
x(k ) , |
|
|
||||||
1 |
11 |
1 |
12 |
2 |
1n |
n |
1 |
|
|
|
|||||
|
x(k 1) |
|
|
x(k ) |
22 |
x(k ) ... |
2n |
x(k ) |
2 |
, |
|
||||
2 |
|
|
21 1 |
|
2 |
|
n |
|
|
|
|||||
|
x(k 1) |
|
n1 |
x(k ) |
n2 |
x(k ) ... |
nn |
x(k ) |
n |
. |
|
||||
|
n |
|
|
1 |
|
2 |
|
n |
|
|
|
||||
3. Итерации прерываются при выполнении условия |
|
||||||||||||||
|
|| α || |
|
x(k 1) x(k ) |
|
, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
1 || α || |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где 0 - заданная точность, которую необходимо достигнуть при решении задачи, или более простого условия:
43


 x(k 1) x(k )
x(k 1) x(k ) 
 .
.
Теорема 1. (о достаточном условии сходимости метода простых итераций)
Метод простых итераций, реализующийся в процессе последовательных приближений (3.3), сходится к единственному решению исходной системы Ax B при любом начальном приближении x(0) со скоростью не медленнее геометрической прогрессии, если какая-либо норма матрицы α меньше 1, т.е. 
 α
α
 s 1, s 1,2,3 .
s 1, s 1,2,3 .
Обратим внимание, что для обеспечения сходимости можно использовать любую из рассмотренных норм, поскольку, если хотя бы одна из ни меньше 1, то это означает, что и все остальные будут меньше 1.
Условие Теорема 1, как достаточное (но не необходимое!) предъявляет завышенные требования к матрице α и поэтому сходимость иногда будет, даже если 
 α
α
 1.
1.
Условия сходимости выполняются, если в исходной матрице A диагональные элементы преобладают, т.е.
|
n |
|
| aii |
| | aik | , i 1,..., n , |
(3.4) |
|
k 1 |
|
причем, по крайней мере, для одного i неравенство строгое. |
|
|
Теорема 2 (о необходимом и достаточном условии сходимости метода простых |
||
итераций) |
|
|
Для |
сходимости последовательности (3.3) при любом x(0) |
необходимо и |
достаточно, чтобы собственные значения матрицы α были по модулю меньше единицы,
т.е. i (α) 1, i 1,..., n .
Хотя эта теорема дает более общие условия сходимости метода простых итераций, чем Теорема 1., однако ею воспользоваться сложнее, поскольку нужно предварительно вычислить границы собственных значений матрицы или сами собственные значения.
Теорема 3. (о погрешности приближений, вычисляемых методом простых итераций)
Если в итерационном процессе норма матрицы α , согласованная с нормой вектора x , меньше единицы ( 
 α
α
 1), то справедлива следующая оценка погрешности:
1), то справедлива следующая оценка погрешности:
x(k ) x* |
|
|
|| α || |
|
|
|
x(k 1) |
x(k ) |
|
. |
|
|
|
|
|
||||||
|
1 || α |
|| |
||||||||
|
|
|
|
|
|
|
|
|||
Это соотношение может быть переписано через начальное приближение x(0) β :
x(k ) x* |
|
|
|| α ||k 1 |
|
|
|
|
β |
|
. |
|
|
|
|
|||||||
|
1 || α || |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
На основе этого можно записать априорную оценку погрешности
|| α ||k 1 |
β |
1 || α || |
из которой еще до расчетов можно получить количество итераций k , требуемых для
44

достижения заданной точности:
k 1 lg lg(1 || α ||) lg 
 β
β
 . lg || α ||
. lg || α ||
Преобразование системы Ax B к виду x = αx + β с матрицей α ,
удовлетворяющей условиям сходимости, может быть выполнено несколькими способами. Приведем способы, используемые наиболее часто.
1. Уравнения, входящие в систему Ax B переставляются так, чтобы выполнялось условие преобладания диагональных элементов (3.4) (для той же цели можно использовать другие элементарные преобразования). Затем, первое уравнение разрешается относительно x1 , второе - относительно x2 и т.д. При этом получается матрица α с нулевыми диагональными элементами.
Например, система
2.8x1 x2 4x3 60, 10x1 x2 8x3 10,
x1 2x2 0.6x3 20
спомощью перестановки уравнений приводится к виду
10x1 x2 8x3 10,x1 2x2 0.6x3 202.8x1 x2 4x3 60,
Теперь диагональные элементы преобладают. Выражаем неизвестные:
x1 0x1 0.1x2 |
0.8x3 |
1, |
|
||||
x2 |
0.5x1 |
0x2 |
0.3x3 |
10 |
|
||
x3 |
0.7x1 |
0.25x2 |
0x3 |
15, |
|
||
Здесь |
|
|
|
|
|
|
|
|
0 |
0.1 |
|
0.8 |
1 |
||
α 0.5 |
0 |
|
0.3 |
|
, β 10 . |
||
|
|
|
|
|
|
|
|
|
0.7 |
0.25 |
0 |
|
15 |
||
|
|
|
|
|
|
|
|
Заметим, что 
 α
α
 1 max{0.9;0.8;0.95} 0.95 1, т.е. условие теоремы 3.1 выполнено.
1 max{0.9;0.8;0.95} 0.95 1, т.е. условие теоремы 3.1 выполнено.
Пример других элементарных преобразований: Пусть дана система
4x1 x2 9x3 7, |
( A) |
3x1 8x2 7x3 6, |
(B) |
x1 x2 8x3 7 |
(C) |
Новую систему с диагональным преобладанием можно получить путем выполнения следующих элементарных преобразований.
45

5x1 2x2 x3 0, |
( A) (C) |
|
|
|
|
2x1 7x2 x3 13, |
(B) (C) |
|
|
|
|
x1 x2 8x3 7 |
(C) |
|
|
|
|
2. Если det A 0 , |
то систему следует умножить на матрицу |
D A 1 |
ε , |
где ε - |
|
матрица с малыми по модулю элементами. Тогда получаемая система |
(A 1 |
ε)Ax DB |
|||
или A 1 Ax εAx DB , которую можно записать в форме x = αx + β , |
где |
α εA , |
β DB . |
||
Если | ij |, i, j 1,..., n , достаточно малы, то условие сходимости выполняется. |
|
|
|||
З а м е ч а н и я. |
|
|
|
|
|
1)Начальное приближение может выбираться произвольно или из некоторых соображений. В частности, в качестве начального приближения можно взять решение, полученное прямым методом.
2)Сходящийся процесс обладает свойством самоисправляемости, т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, т.к. ошибочное приближение можно рассматривать как новое начальное.
3)Чем меньше величина нормы 
 α
α
 , тем выше скорость сходимости метода.
, тем выше скорость сходимости метода.
4.1.3.Метод Гаусса-Зейделя
Этот метод является модификацией метода простых итераций и в некоторых случаях приводит к более быстрой сходимости.
Итерации по методу Зейделя отличаются от простых итераций тем, что при нахождении i -й компоненты (k 1) -го приближения сразу используются уже найденные компоненты этого (k 1) -го приближения с меньшими номерами 1, 2,...,i 1.
В развернутой форме данный процесс записывается в виде:
|
|
|
|
|
|
x(k 1) |
|
x(k ) |
x(k ) x(k ) ... x(k ) |
, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
11 1 |
12 2 |
13 3 |
|
1n n |
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
x(k 1) |
|
x(k 1) |
|
x(k ) |
|
|
x(k ) ... |
|
x(k ) |
, |
|
|
|
||||
|
|
|
|
|
|
2 |
|
21 1 |
|
22 2 |
|
23 3 |
|
2n n |
2 |
|
|
|
|
||||
|
|
|
|
|
|
x(k 1) |
|
x(k 1) |
|
x(k 1) |
|
|
x(k ) ... |
|
x(k ) |
, |
|
|
|||||
|
|
|
|
|
|
3 |
|
31 1 |
|
32 2 |
|
|
33 3 |
|
|
2n n |
|
2 |
|
|
|
||
|
|
|
|
|
|
x(k 1) |
|
x(k 1) |
|
x(k 1) |
|
x(k 1) |
... |
x(k ) |
|
n |
. |
||||||
|
|
|
|
|
|
n |
|
n1 1 |
|
n2 2 |
|
|
|
n3 3 |
|
|
|
nn n |
|
|
|
|
|
|
|
|
|
|
|
Т.е. в каждое последующее уравнение подставляются значения неизвестных, |
|||||||||||||||||
полученных из предыдущих уравнений. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Теорема 4 (о достаточном условии сходимости метода Зейделя) |
|||||||||||||||||
|
|
|
|
|
|
Если для системы x = αx + β какая-либо норма матрицы α меньше единицы, т.е. |
|||||||||||||||||
|
α |
|
|
|
s |
1, s 1, 2,3 , |
то процесс итерации Гаусса-Зейделя сходится к единственному |
||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
решению исходной системы Ax B при любом начальном приближении x(0) . |
|||||||||||||||||||||||
|
|
|
|
|
|
В матричной форме процесс итераций Гаусса-Зейделя можно записать следующим |
|||||||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x(k 1) Lx(k 1) Ux(k ) β , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
L,U являются разложением матрицы α : |
|
|
|
|
|
|
|
|||||||||||||||
46
0 |
0 |
0 |
... |
0 |
11 |
12 |
13 ... |
||||||||
|
|
0 |
0 |
... |
0 |
|
|
0 |
|
|
|
|
... |
||
|
21 |
|
|
|
|
|
|
|
|
|
|
22 |
|
23 |
|
L 31 |
32 |
0 |
... |
0 |
|
, U |
0 |
0 |
33 ... |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... ... |
... |
... |
... |
... ... ... ... |
|||||||||||
|
n1 |
|
n2 |
|
n3 |
... |
0 |
|
|
0 |
0 |
0 ... |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Преобразуя |
|
эту |
|
систему |
к виду |
|
x = αx + β , |
||||||||
итерационного процесса метода Гаусса-Зейделя:
1n
2n
3n
...
nn
получаем матричную форму
x(k 1) (E L) 1Ux(k ) (E L) 1β .
Тогда достаточное условие сходимости (Теорема 1) будет иметь вид:

 α
α


 (E L) 1U
(E L) 1U 
 1 ,
1 ,
а необходимое и достаточное (Теорема 2) :

 i (α)
i (α)


 i (E L) 1U
i (E L) 1U 
 1.
1.
Метод Гаусса-Зейделя имеет преимущество перед методом простых итераций, т.к. он всегда сходится для нормальных СЛАУ, т.е. таких систем, в которых матрица A является симметрической и положительно определенной. СЛАУ с невырожденной матрицей A всегда можно преобразовать к нормальной, если ее умножить слева на матрицу AT .
Таким образом, система AT AX AT B является нормальной, а матрица AT A симметричной и положительно определенной.
4.1.4. Проверка сходимости на каждом шаге
(для метода простых итераций и метода Гаусса-Зейделя):
Процесс итераций сходится, если максимальная по модулю разность между отдельными компонентами решения на каждом шаге убывает, т.е.
max |
(k ) max |
(k 1) , где |
(k ) |
x(k ) x(k 1) |
, k 1, 2,... . |
|||
1 i n |
i |
1 i n |
i |
i |
|
i |
i |
|
|
|
|
|
|
|
|
||
4.2. ЗАДАНИЕ НА РАБОТУ
Решить систему линейных алгебраических уравнений:
a11x1 a12x2 a13x3 b1a21x1 a22x2 a23x3 b2
a31x1 a32x2 a33x3 b3
методами:
1.Простых итераций
2.Гаусса-Зайделя
4.3. ВАРИАНТЫ ЗАДАНИЙ
см. занятие 3.
47
4.4.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что называется решением СЛАУ?
2.Каковы условия существования решения СЛАУ?
3.Каковы условия единственности решения СЛАУ?
4.В чем заключается основная идея итерационных методов решения СЛАУ?
5.Что понимается под сходимостью итерационных методов решения СЛАУ?
6.Каким образом можно контролировать сходимость итерационного процесса на каждой итерации?
7.В чем состоит метод простой итерации для решения систем линейных уравнений?
8.В чем состоит метод Гаусса-Зайделя для решения систем линейных уравнений?
9.Какова сложность метода простой итерации?
10.Какова сложность метода Гаусса-Зайделя?
11.Какой метод эффективнее – метод простой итерации или метод Гаусса-Зайделя?
48
5.ЗАНЯТИЕ 4. АЛГЕБРАИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
5.1.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
5.1.1.Постановка задачи интерполяции
Пусть на отрезке [a,b] задана сетка |
|
a x0 x1 ... xn b и |
в ее |
узлах |
заданы |
|||
значения f(x): |
y0 f (x0 ) , y1 |
f (x1 ) ,…, yi |
f (xi ) ,…, yn |
f (xn ) . Пусть на [a,b] |
задано |
|||
также некоторое семейство функций F(x,c ), |
c (c ,...,c )T вектор параметров, значение |
|||||||
|
|
|
|
0 |
n |
|
|
|
которого определяет конкретную функцию из этого семейства. |
|
|
|
|||||
Требуется |
определить |
значения |
свободных |
параметров |
c |
так, |
чтобы |
|
аппроксимирующая функция (интерполента) |
F(x,c ) совпадала с f(x) в узлах сетки: |
|||||||
|
F(xi ,c ) f (xi ), |
i 0,1, ,n . |
|
|
(5.1) |
|||
Система условий (5.1) называется условиями интерполяции.
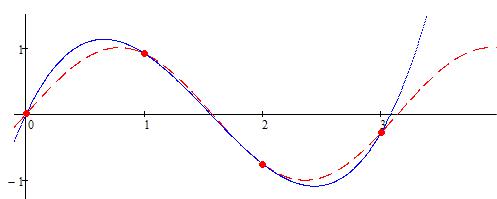
Геометрически требование выполнения условий интерполяции означает (Рисунок 5.1), что нужно найти кривую F(x), проходящую через заданную систему точек.
y F(x)
y
y f (x)
x |
x |
x |
x |
x |
Рисунок 5.1 – Сущность интерполяции
Основная цель интерполяции: получить быстрый (экономичный) алгоритм приближенного вычисления значений f(x) для значений x не содержащихся в таблице данных или получить аналитическую зависимость F(x,c ) , более удобную для дальнейшего анализа по сравнению с f(x).
Для удобства дальнейших вычислений интерполирующая функция, как правило, строится как линейная комбинация некоторых фиксированных функций, называемых базисными:
n |
|
F (x,c ) ck k (x) |
(5.2) |
k 0
где k (x) , k=0,1,…,n – фиксированная система базисных функций.
Для существования и единственности решения задачи интерполяции необходимо и достаточно, чтобы система базисных функций была линейно-независимой на [a,b] .
Одной из типичных линейно-независимых систем функций является система
49
степенных функций: (x) 1, |
(x) x,..., (x) xn . |
|
|
0 |
1 |
k |
|
Многочлен по степенному базису |
(x) xk , k 0,..., n |
|
|
|
|
k |
|
n |
n |
|
|
F (x,c ) ck k (x) ck xk c0 c1x c2 x2 ... cn xn Pn (x) |
(5.3) |
||
k 0 |
k 0 |
|
|
называется полиномом степени n .
Интерполяция полиномом называется полиномиальной или алгебраической интерполяцией.
5.1.2. Интерполирование по Вандермонду
Интерполирование по Вандермонду заключается в нахождении коэффициентов интерполяционного полинома (5.3) путем непосредственного решения системы уравнений, составленной по условиям интерполяции.
В случае интерполяции полиномом (5.3), условия интерполяции будут иметь вид:
c c x c x2 |
... |
c xn f (x ), |
|
|||
0 |
1 0 |
2 0 |
|
n 0 |
0 |
|
c c x c x2 ... |
c xn f (x ), |
(5.4) |
||||
0 |
1 1 |
2 1 |
|
n 1 |
1 |
|
|
|
|||||
. . . . . . . . . . . . . . . . . . . . . . . . . . |
|
|||||
c c x c x2 |
... |
c xn f (x ). |
|
|||
0 |
1 n |
2 n |
|
n n |
n |
|
Определитель матрицы коэффициентов при неизвестных СЛАУ (5.4) называется определителем Вандермонда и всегда отличен от 0 при условии, что среди узлов нет совпадающих.
|
1 |
x |
... |
xn |
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
det |
1 |
x |
... |
xn |
0 |
, если x |
x |
i, j 0,...,n; i j |
|
1 |
|
1 |
|||||
|
... ... ... ... |
|
i |
j |
|
|||
|
|
|
|
|
||||
|
1 |
x |
... |
xn |
|
|
|
|
|
|
n |
|
n |
|
|
|
|
Следовательно, решение системы (5.4) существует и единственно. Тогда, решив ее любым методом решения СЛАУ можно найти искомые коэффициенты интерполяционного полинома c0 ,c1 ,...,cn .
Пример 5.1
Дана таблица значений функции y = x2 + 4x - ex .
i |
xi |
yi |
|
|
|
0 |
0,0 |
-1,0000 |
1 |
0,5 |
0,6013 |
2 |
1,0 |
2,2817 |
3 |
1,5 |
3,7683 |
4 |
2,0 |
4,6109 |
|
|
|
Для узлов 0,1,3 построить интерполирующий многочлен, используя интерполирование по Вандермонду и определить с его помощью значение функции при x=0.7.
50
