
MU_LR_VychMat_230400
.pdfРешение. Искомый интерполирующий полином имеет вид: P2 (x) c0 c1x c2 x2 .
В соответствии с условиями интерполяции, система уравнений для нахождения коэффициентов полинома будет иметь вид:
c c x |
c x 2 |
y , |
||||
0 |
1 |
0 |
2 |
0 |
0 |
|
c c x |
c x 2 |
y , |
||||
0 |
1 |
1 |
2 |
1 |
1 |
|
c c x |
c x 2 |
y |
. |
|||
0 |
1 |
2 |
2 |
2 |
2 |
|
Подставляя в систему исходные данные, получим:
c c 0 c 02 1, |
|||||||
0 |
|
1 |
2 |
|
|
|
|
c |
|
c 0.5 |
c |
|
0.52 |
0.6013, |
|
0 |
|
1 |
2 |
|
|
||
c |
|
c 1.5 |
c |
|
1.52 |
3.7683. |
|
0 |
|
1 |
2 |
|
|
|
|
Определитель Вандермонда: |
|||||||
|
|
0 |
0 |
|
|
|
|
|
1 |
|
|
|
|
||
det |
1 |
0.5 |
0.52 |
|
0.75 0 . |
||
|
1 |
1.5 |
1.52 |
|
|
|
|
Решение системы:
c0 1, c1 |
3.2145, c2 0.0237 . |
|
|
|
|||
Искомый интерполяционный полином: |
|
|
|
||||
P (x) 1 3.2145x – 0.0237x2 . |
|
|
|
||||
2 |
|
|
|
|
|
|
|
Проверка выполнения условий интерполяции: |
|
||||||
P (0) 1 3.2145 0 – |
0.0237 02 1 |
f (0), |
|
||||
2 |
|
|
|
|
|
|
|
P (0.5) |
1 |
3.2145 0.5 |
– |
0.0237 0.52 |
|
0.601325 0.601 f (0.5), |
|
2 |
|
|
|
|
|
|
|
P (1.5) |
1 |
3.2145 1.5 |
– |
0.0237 1.52 |
|
3.768425 3.768 |
f (1.5) |
2 |
|
|
|
|
|
|
|
Значение функции при x = 0,7: P2 0.7 |
1.2385 . |
|
|||||
5.1.3. Интерполирование по Лагранжу
Непосредственное нахождение коэффициентов ck с помощью решения системы уравнений уже при n=20, приводит к достаточно сильному их искажению вычислительной погрешностью. Поэтому применяются другие способы построения интерполяционного полинома. В частности, интерполяционный многочлен может быть представлен в форме Лагранжа:
n |
n |
x xj |
|
||
Ln (x) f (xk ) |
|
|
|
||
x |
x |
|
|||
k 0 |
j 0 |
j |
|||
k |
|
||||
|
j k |
|
|
|
|
Эта формула легко программируется.
Пример 5.2 Для узлов 0,1,3 из примера 5.1 построить интерполирующий полином, используя метод Лагранжа, и с его помощью рассчитать значение функции при x=0.7 .
Решение. Многочлен Лагранжа для заданных узлов имеет вид :
51

P2 (x) |
(x x1 )(x x3 ) |
|
f (x0 ) |
(x x0 )(x x3 ) |
f (x1 ) |
(x x0 )(x x1 ) |
f (x3 ) |
|||||||
(x0 x1 )(x0 |
x3 ) |
(x1 x0 )(x1 x3 ) |
(x3 x0 )(x3 x1 ) |
|||||||||||
|
|
|
|
|
|
|
||||||||
(x 0.5)(x 1.5) |
|
( 1) |
|
(x ( 1))(x 1.5) |
0.6013 |
|
(x ( 1))(x 0.5) |
3.7683 |
||||||
( 1 0.5)( 1 1.5) |
|
(0.5 ( 1))(0.5 1.5) |
(1.5 ( 1))(1.5 0.5) |
|||||||||||
|
|
|
|
|
|
|||||||||
После преобразований получаем: P2 (x) 1 3.2145x – 0.0237x2 .
Значение функции при x= 0,7 : P2 0.7 1.2385 .
5.1.4. Интерполяционный полином Ньютона с разделенными разностями
Интерполяционным многочленом Ньютона называется многочлен
Pn (x) f (x0 )+(x x0 ) f (x0 , x1 )+(x x0 )(x x1 ) f (x0 , x1, x2 )+ +(x x0 ) ... (x xn 1 ) f (x0 , x1,..., xn ),
где f (x0 , x1 ) , f (x0 , x1, x2 ) ,…, f (x0 , x1,..., xn ) – разделенные разности, которые могут быть вычислены рекуррентно по следующим формулам.
Разделенная разность нулевого порядка функции f (x) – сама функция f (x) . Разделенная разность n -го порядка определяется через разделенную разность n 1-го порядка по формуле:
Кроме того, любую разделенную разность можно вычислить напрямую:
Примеры разделенных разностей 1-го порядка:
f (x , x ) |
f (x1 ) f (x0 ) |
, |
f (x , x ) |
f (x3 ) f (x2 ) |
|
|
||
|
|
|||||||
|
|
|
||||||
0 |
1 |
x1 x0 |
2 |
3 |
x3 x2 |
|
||
|
|
|
|
|
||||
5.1.5. Интерполяционный полином Ньютона с конечными разностями |
||||||||
Для |
равномерной сетки, |
когда hi 1 const h и |
xi x0 ih , интерполяционный |
|||||
полином Ньютона с разделенными разностями может быть выражен через конечные разности.
Введем вспомогательную переменную q x x0 , называемую фазой интерполяции. h
Кроме того, для краткости введем обозначение fi |
f (xi ) . |
||||||||||
Интерполяционный полином Ньютона с конечными разностями для |
|||||||||||
интерполирования вперед имеет вид: |
|
|
|
|
|||||||
P (q) |
f |
|
|
f |
0 q |
2 f |
0 q(q 1) ... |
n f |
0 |
q(q 1) |
... (q n 1) , |
0 |
|
|
|
|
|||||||
n |
|
|
1! |
2! |
|
n! |
|
|
|
||
|
|
|
|
|
|
|
|
||||
где f , 2 f ,..., n f |
– конечные разности, которые могут быть определены рекуррентно в |
||||||||||
соответствии с формулами: |
|
|
|
|
|
||||||
52
Конечная разность первого порядка: fi fi 1 fi
Конечная разность второго порядка: 2 fi ( fi ) fi 1 fi
Конечная разность k -го порядка. k f |
i |
( k 1 f |
) k 1 f |
i 1 |
k 1 f |
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|||
Если фазу интерполирования определить |
относительно |
узла x |
: |
qˆ |
x xn |
, то |
|||||
|
|||||||||||
|
|
|
|
|
|
|
|
n |
|
h |
|
|
|
|
|
|
|
|
|
|
|
||
получим аналогичное выражение, определяющее интерполяционный полином Ньютона с конечными разностями для интерполирования назад.
P (qˆ) f |
|
|
f |
n 1 |
qˆ |
|
2 f |
n 2 |
qˆ(qˆ |
1) ... |
n f |
0 |
qˆ(qˆ |
1) ... (qˆ n 1) . |
n |
|
|
|
|
|
|
||||||||
n |
|
1! |
|
|
2! |
|
|
n! |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Данная формула применяется для вычисления значений функции в правой части отрезка интерполяции.
5.1.6. Построение плоского графика функции в MathCad
Для построения плоского графика функции надо:
-Установить крестообразный курсор в то место, где надо построить график.
-На математической панели щелкнуть мышью на кнопке Graph Toolbar / X-Y Plot (Плоский график).
-В появившемся на месте курсора шаблоне плоского графика введите на оси абсцисс имя аргумента, на оси ординат имя функции.
-Щелкните мышью вне шаблона графика. График построен для заданного диапазона изменения аргумента.
Если диапазон значений аргумента не задан, по умолчанию график будет построен в диапазоне значений аргумента от –10 до 10 .
Чтобы в одном шаблоне разместить насколько графиков надо, набрав на оси ординат имя первой функции, нажать клавишу запятая (уголок курсора при этом обязательно должен находиться в конце имени функции). В появившемся месте ввода (черном квадратике) впишите имя второй функции и так далее.
Кроме того, начиная с версии Mathcad 12 появилась возможность добавления на графике справа второй оси ординат со своей собственной шкалой.
Если две функции имеют разные аргументы, например, f1 (x) и f2 ( y) , то на оси ординат ввести (через запятую) имена обеих функций, а на оси абсцисс (также через запятую) ввести имена обоих аргументов x и y. Тогда первый график будет построен для первой функции по первому аргументу, второй график для второй функции по второму аргументу. Если ввести на осях ординат и абсцисс имена двух функций одного аргумента, то будет построен параметрический график функции. В частности, таким образом можно отобразить таблично-заданную функцию.
Если функций введено несколько, а аргументов 2, то график первой функции строится по первому аргументу, графики остальных функций по второму аргументу.
На рисунке 5.2 приведен пример построения графиков интерполируемой и интерполирующей функции с указанием узлов интерполяции.
53
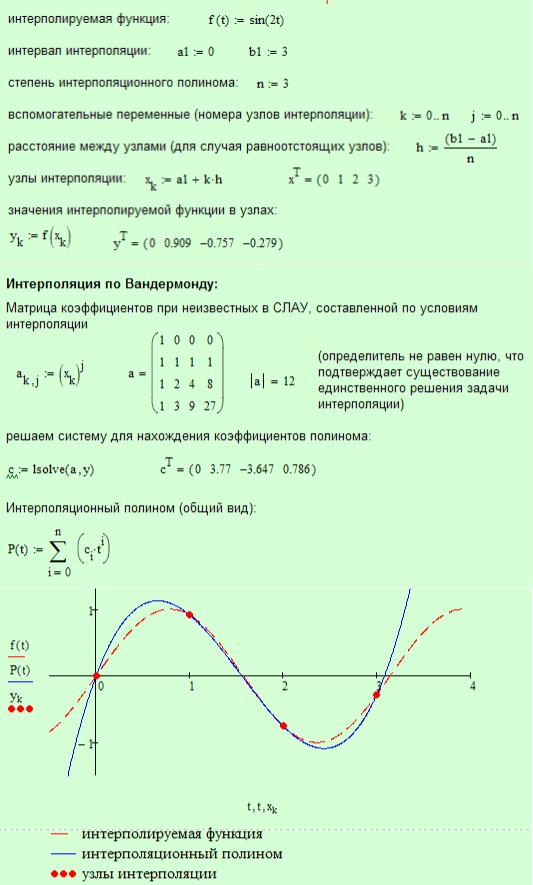
Рисунок 5.2 – Пример построения плоских графиков в MathCad при решении задачи интерполяции
54
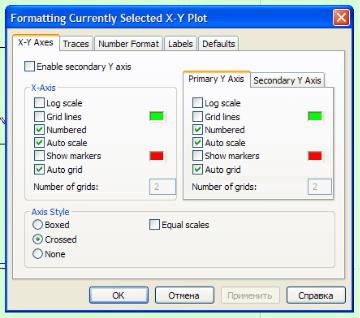
Чтобы отформатировать график, сделайте двойной щелчок мышью в поле графика – откроется окно форматирования графика (рис. 5.3) или щелчок правой кнопкой мыши и во всплывающем меню выберите пункт format.
Рисунок 5.3 – Окно настройки формата плоского графика в MathCad
В открывшемся окне (рис. Рисунок 5.3) видны заголовки четырех вкладок:
1)X-Y Axes – отформатировать оси координат: нанести сетку линий, проставить численные значения; ось абсцисс провести через ноль ординаты (Crossed) или по нижнему краю графика (Boxed), нанести метки на графике. Щелкните мышью на нужных пунктах подменю (пометьте их птичкой).
Log Scale – представить численные значения на осях в логарифмической шкале. По умолчанию численные значения наносятся в равномерной шкале.
Grid Lines – нанести сетку линий.
Numbered – нанести численные значения для каждой линии сетки.
Auto Scale – автоматически выбирает предельные численные значения на осях, большие максимальных вычисленных значений.
Autogrid – число линий сетки выбирается автоматически. Если пункт не отмечен, надо задать число линий Number of Grids.
Show Markers – нанести метки на графике. На каждой оси появляются 2 места ввода,
вкоторые можно ввести численные значения (можно не вводить ничего или ввести одно число или буквенные обозначения констант). На графике появятся горизонтальные или вертикальные пунктирные линии, соответствующие указанному значению на оси. В конце этой линии появляется само число (рис. 14).
2)Traces – отформатировать графики функций. Для каждого графика в отдельности можно изменить:
вид линии: Solid – сплошная, Dot – пунктир, Dash – длинный пунктир, Dadot – штрих-пунктир.
Цвет линии (Color).
55
Тип графика (Type) : Lines – линия, Points – точки, Bar или Solidbar – столбики, Step
– ступенчатый график и другие. Толщину линии (Weight).
Расчетные точки отметить символом на графике (Symbol) – кружком, крестиком, прямоугольником, ромбом.
3)Вписать в область графика заголовок (Label). В окне Title (Заголовок) записать текст заголовка. Выбрать его положение – вверху или внизу графика. Вписать, если надо, названия аргумента и функции (Axis Label).
4)Defaults – вернуться к виду графика, принятому по умолчанию (Change to default), либо сделанные вами изменения на графике использовать по умолчанию для всех графиков данного документа (Use for default).
5.2. ЗАДАНИЕ
Построить интерполяционный полином по значениям функции f (x) в 4-х узлах
1)по Вандермонду (путем непосредственного решения системы линейных уравнений, составленных по условиям интерполяции);
2)по Лагранжу;
3)полином Ньютона с разделенными разностями;
4)полином Ньютона с конечными разностями.
Результат представить в виде формулы интерполяционного многочлена и графически в среде MathCad. На графике пунктирной линией показать исходную интерполируемую функцию, отметить узлы интерполяции, и сплошной линией показать найденный интерполяционный многочлен.
5.3.ВАРИАНТЫ ЗАДАНИЙ
1.f (x) 3x3 2x 5 , на интервале [ 2,1]
2.f (x) 5x3 2x2 1 , на интервале [ 3, 0]
3.f (x) 2x4 x3 , на интервале [ 2,1]
4.f (x) x4 3x 1 , на интервале [2,3.5]
5.f (x) 5x3 3x 1, на интервале [0; 6]
6.f (x) x3 3x 1, на интервале [ 2; 4]
7.f (x) x3 3x2 4 , на интервале [ 2; 4]
8.f (x) 4x2 2x 5 , на интервале [0;6]
9.f (x) x4 x2 3x 1, на интервале [ 1, 2]
10.f (x) x4 2 , на интервале [ 2,1]
11.f (x) 5x3 2x2 1 , на интервале [ 1, 2]
56
12.f (x) 3x3 2x 5 , на интервале [0,3]
13.f (x) sin 2x cos 2x 1 , на интервале [ ; / 2]
14.f (x) 2sin x cos 2x 3, на интервале [0;3 / 2]
15.f (x) 3(sin 2x cos x) , на интервале [ ; / 2]
16.f (x) 3sin x cos x 2 , на интервале [ ; / 2]
17.f (x) sin 2x 3cos 2x , на интервале [ ; / 2]
18.f (x) sin 2x cos 2x 1, на интервале [0;3 / 2]
19.f (x) 2sin x cos 2x 3, на интервале [ ; / 2]
20.f (x) 3(sin 2x cos x) , на интервале [0;3 / 2]
21.f (x) 3sin x cos x 2 , на интервале [0;3 / 2]
22.f (x) sin 2x 3cos 2x , на интервале [0;3 / 2]
23.f (x) ex , на интервале [ 2,1]
24.f (x) e x , на интервале [ 1, 2]
25.f (x) e 0.1x 1, на интервале [ 2,1]
26.f (x) e 0.1x 1, на интервале [0,3]
27.f (x) 2e 0.2x 1 , на интервале [ 2,1]
28.f (x) 2e 0.1x 1, на интервале [0,3]
29.f (x) ex 2 , на интервале [ 2,1]
30.f (x) e x 1, на интервале [ 1, 2]
5.4.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.В чем заключается задача интерполяции?
2.Что понимается под экстраполяцией?
3.Сформулируйте условия интерполяции.
4.Сформулируйте необходимые и достаточные условия существования и единственности решения задачи интерполяции.
5.Что такое полиномиальная интерполяция?
6.Что представляет собой интерполяционный полином Лагранжа?
7.Дайте определение конечных разностей.
8.Дайте определение разделенных разностей.
9.Укажите взаимосвязь конечных и разделенных разностей.
10.Что представляет собой интерполяционный многочлен Ньютона с разделенными
иконечными разностями?
11.В каких случаях удобнее применять метод Ньютона?
12.В каких случаях удобнее применять интерполяционную формулу Лагранжа?
57
6.ЗАНЯТИЕ 5. ИНТЕРПОЛИРОВАНИЕ СПЛАЙНАМИ
6.1.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
6.1.1.Построение интерполяционного кубического сплайна
Сплайном (интерполяционным кубическим сплайном), соответствующим заданной
функции f (x) и заданным узлам a x0 x1 ... xn |
b |
называется кусочно- |
полиномиальная функция S(x) , удовлетворяющая следующим условиям: |
||
1) на каждом сегменте xi 1 , xi , i 1,2, , n функция |
S(x) |
является многочленом |
третьей степени;
2)функция S(x) , и ее первая и вторая производные непрерывны на отрезке [а,b];
3)условия интерполяции: S(xi ) f (xi ),i 0,...,n .
На каждом отрезке xi 1 , xi , i 1,2, , n будем искать |
S(x) Si (x) в виде |
|
||||||||||
|
|
S (x) a |
b (x x ) |
ci |
(x x )2 |
|
di |
(x x )3 |
(6.1) |
|||
|
|
|
|
|||||||||
|
|
i |
i |
i |
i |
2 |
i |
6 |
i |
|
||
|
|
|
|
|
|
|
|
|
||||
xi 1 |
x |
xi , i 1,2,..., n , |
где |
ai ,bi ,ci ,di |
- коэффициенты, подлежащие |
определению. |
||||||
Всего 4n коэффициентов. Однако согласно условиям интерполяции, ai fi , т.е. на самом деле остается найти 3n коэффициентов. Однако на основе условий (1-2) из определения интерполяционного кубического сплайна могут быть получены всего (3n-2) уравнений. Для того, чтобы система имела решение вводят дополнительные, так называемые граничные условия. Например, типичным является условие c0 cn 0 .
Задача сплайн-интерполяции может быть сведена к решению системы уравнений относительно неизвестных ci и последующему выражению через них остальных искомых коэффициентов.
Введем дополнительные обозначения: hi xi xi 1 , i 1,..., n .
С учетом данных обозначений, система уравнений для определения коэффициентов ci может быть записана в следующем виде:
h c |
2(h |
h |
)c h c |
6 |
|
fi 1 fi |
|
fi fi 1 |
|
, i 1,..., n 1, c |
c |
0 . |
(6.2) |
|
|
|
|||||||||||
i i 1 |
i |
i 1 |
i i 1 i 1 |
|
|
hi 1 |
hi |
0 |
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
Это система из (n-1) уравнений с (n-1) неизвестными. Следует отметить, что ее матрица коэффициентов при неизвестных является трехдиагональной и может быть легко решена методом прогонки.
Остальные неизвестные коэффициенты могут быть найдены по формулам:
|
|
|
c c |
; b |
h |
c |
h2 |
|
|
|
f |
i |
f |
i 1 |
|
d |
|
i i 1 |
i |
i |
d |
|
|
|
, i=1,2,…, n . |
||||||
|
i |
|
h |
i |
2 |
i |
6 |
|
i |
|
|
|
h |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
i |
|
|
58

6.1.2. Интерполяция сплайнами в MathCad
Для полиномиальной сплайн-интерполяции в MathCad используются следующие функции.
Векторы х и y имеют тот же смысл, что и соответствующие аргументы функции interp.
Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала. Пример сплайн-интерполяции:
6.2.ЗАДАНИЕ
1.Построить интерполяционный кубический сплайн по значениям функции в 7-ми узлах. График построенного сплайна и исходной функции построить при помощи
MathCad.
2.Построить интерполяционный кубический сплайн при помощи встроенных функций MathCad.
6.3.ВАРИАНТЫ ЗАДАНИЙ
59
см. занятие 5.
6.4.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.В чем заключается задача интерполяции?
2.Что понимается под экстраполяцией?
3.Сформулируйте условия интерполяции.
4.Сформулируйте необходимые и достаточные условия существования и единственности решения задачи интерполяции.
5.Что такое полиномиальная интерполяция?
6.Что понимают под сходимостью процесса интерполяции?
7.Что понимают под кусочно-полиномиальной интерполяцией?
8.Что такое интерполяционный кубический сплайн?
9.Как построить интерполяционный кубический сплайн?
10.Какие предположения лежат в основе построения интерполяционного кубического сплайна?
11.Какими свойствами обладает интерполяционный кубический сплайн?
60
