MU_LR_VychMat_230400

7. ЗАНЯТИЕ 6. СРЕДНЕКВАДРАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ ФУНКЦИЙ

7.1.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

7.1.1.Постановка задачи среднеквадратического приближения

значение которого определяет конкретную функцию из этого семейства, причем n N .

Задачу среднеквадратического приближения также называют задачей регрессионного анализа.

Принципиальное отличие задачи среднеквадратичного приближения от задачи интерполяции заключается в том, что число неизвестных параметров аппроксимирующей

7.1.2. Метод наименьших квадратов

Задача (7.1) является задачей оптимизации функции нескольких аргументов при

Приравняв полученные производные к нулю, получим систему уравнений для нахождения координат стационарной точки:

61

Конкретный вид системы уравнений определяется видом аппроксимирующей функции F(x,c ) .

Поскольку минимизируемая функция является квадратичной, то найденная путем решения системы стационарная точка с координатами c0 ,...,cn является точкой минимума критерия J (c ) и, соответственно, решением задачи среднеквадратичного приближения

(7.1).

7.1.3.Среднеквадратическое приближение многочленами

Вкачестве параметрического семейства F(x,c ) может быть выбрана любая

подходящая (согласующаяся с исходными данными) эмпирическая формула, например,

Однако, как и при решении задачи интерполяции, в качестве аппроксимирующей функции часто применяют многочлены по некоторому базису:

k 0

где k (x) , k=0,1,…,n – фиксированная система базисных функций.

В этом случае система уравнений (7.2) будет системой линейных алгебраических уравнений и примет вид:

Определитель матрицы коэффициентов при неизвестных системы (7.4), составленный из скалярных произведений, называется определителем Грамма. В теории функций доказывается, что он отличен от нуля тогда и только тогда, когда система функций k (x) , k=0,1,…,n является линейно независимой.

Таким образом, для того, чтобы задача среднеквадратического приближения многочленом по базису функций k (x) , k=0,1,…,n имела единственное решение необходимо и достаточно, чтобы система функций k (x) , k=0,1,…,n была линейно независимой на множестве узлов аппроксимации. Наиболее типичными примерами линейно независимых систем функций является система степенных 1, x,..., xk и система тригонометрических базисных функций 1, sin(x) , cos(x) , sin(2x) , cos(2x) ,… .

Если же система базисных функций является не только линейно независимой, но и ортогональной или ортонормированной на множестве узлов аппроксимации, то решение

62

системы (7.4) существенно упрощается, поскольку она распадается на n 1 независимых уравнений.

Две функции k (x) и j (x) называются ортогональными на некотором множестве точек x0 ,..., xN , среди которых нет совпадающих, если их скалярное произведение на этом множестве точек равно нулю:

Система функций k (x) , k=0,1,…,n называется ортогональной на множестве точек x0 ,..., xN , если скалярные произведения всех пар несовпадающих функций из базисной системы на данном множестве точек равны нулю:

Система функций k (x) , k=0,1,…,n называется ортонормированной на множестве точек x0 ,..., xN , если она является ортогональной на этом множестве точек и норма каждой из функций равна единице, т.е.

|| k (x) || k , k 1 , k 0,..., n

Вслучае ортогональной системы базисных функций коэффициента аппроксимирующего многочлена могут быть найдены по формулам cj ( f , j ) / ( j , j ) , а

вслучае ортонормированной системы еще проще: cj ( f , j ) .

7.1.4.Система многочленов, ортогональных на равномерной сетке

Вслучае, когда узлы, по которым производится аппроксимация, являются равноотстоящими, в качестве системы ортогональных многочленов можно использовать

Тогда аппроксимирующий полином, составленный из полиномов Чебышева примет

вид:

63

7.1.5. Работа с файлами в MathCAD

Для общения с внешними файлами данных в MathCAD имеется несколько разных способов. Рассмотрим функции работы с текстовыми файлами.

1)- READPRN(―file‖) – чтение данных в матрицу из текстового файла;

-WRITEPRN(―file‖) – запись данных в текстовый файл;

-APPENDPRN(―file‖) – дозапись данных в существующий текстовый файл, где file – путь к файлу.

Можно задавать как полный(абсолютный) путь к файлу, так и относительный, имея ввиду, что он будет считываться от папки, в которой находится файл с документом

MathCAD.

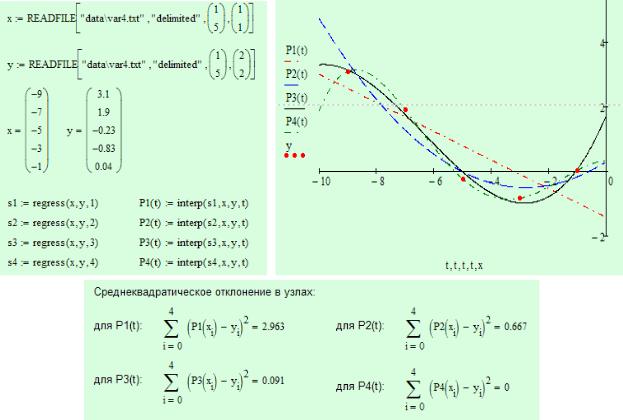
Пример:

а) б)

Рисунок 7.1 – а) текстовый файл и б) считывание данных из него при помощи функции

READPRN

2) Начиная с MathCAD 12 появилась возможность импорта данных из внешнего файла при помощи мастера импорта данных (Data Import Wizard), позволяющего осуществить импорт в нужном формате в диалоговом режиме с подсказками.

Для вызова мастера можно выбрать команду верхнего меню Insert | Component (Вставка | Компонент), а затем указать в списке тип компонента Data Import Wizard. При этом появится окно Мастера, которое в пошаговом режиме позволит осуществить считывание нужной информации (Рисунок 7.2).

64

7.1.6.Среднеквадратическое приближение полиномами произвольной степени

вMathCAD

ВMathcad среднеквадратическое приближение полиномом (полиномиальная регрессия) осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции:

regress (х, у, k) — вектор коэффициентов для построения полиномиальной регрессии данных;

interp(s,x,y, t) — результат полиномиальной регрессии:

s=regress(х,у,k);

x — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;

у — вектор действительных данных значений того же размера;

k — степень полинома регрессии (целое положительное число);

t — значение аргумента полинома регрессии;

ВНИМАНИЕ!

Для среднеквадратического приближения полиномом k-й степени необходимо наличие, по крайней мере, (k+1) точек данных. Для построения полиномиальной регрессии после функции regress обязательно нужно использовать функцию interp.

Рисунок 7.4 – Пример среднеквадратического приближения полиномами разных степеней

66

7.2.ЗАДАНИЕ

1.Выполнить среднеквадратическое приближение исходной функции f (x) ,

Таблицу значений исходной функции для варианта с номером N необходимо взять из прилагающегося файла с названием varN.txt.

План выполнения задания 1:

1)Построить график исходной функции (в виде изолированных точек) в MathCAD и по его виду выбрать наиболее подходящую функцию из предложенного набора (при выборе функции следует учесть изменение их вида при изменении знака коэффициентов).

2)Найти производные критерия среднеквадратического приближения по каждому из параметров c0 ,c1 ,c2 и приравнять к нулю, получив систему уравнений вида (7.2).

3)Полученную в результате выполнения п.2. систему уравнений решить в MathCAD при помощи блока Given … Find (см. раздел «Решение СЛАУ в MathCAD»).

4)Записать полученную аппроксимирующую функцию с учетом найденных коэффициентов.

5)Построить средствами MathCAD на одном графике результирующую аппроксимирующую функцию и узлы аппроксимации.

2.По точкам x0 ,..., x4 исходных данных из файла varN.txt выполнить

среднеквадратическое приближение по степенному базису полиномом второй степени Q2 (x) 1) без использования ортогональных полиномов и 2) с использованием ортогональных полиномов Чебышева.

Рекомендации по выполнению задания 2.

1)при аппроксимации многочленом по не ортогональному базису необходимо составить СЛАУ вида (7.4) и решить ее любым способом (можно в MathCAD при помощи функции lsolve). В качестве результата привести найденную функцию и ее график с указанием узлов аппроксимации.

2)решение выполнить по формулам (7.7)-(7.8). В качестве результата привести найденную функцию и ее график с указанием узлов аппроксимации.

среднеквадратическое отклонение в узлах от исходной функции и представить все полиномы на одном графике, на котором указать также узлы аппроксимации.

67

8. ЗАНЯТИЕ 7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

8.1.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

8.1.1.Постановка задачи численного интегрирования

Пусть дана функция f (x) , непрерывная на [a,b] . Требуется найти значение определенного интеграла

b

I f (x)dx .

a

Численные методы обычно применяются при вычислении интегралов, которые невозможно или трудно взять аналитически или если подынтегральная функция задана не формульно, а, например, таблично или в виде алгоритма вычисления ее значения.

8.1.2. Концепция численного интегрирования

Все численные методы строятся на том, что подынтегральная функция приближенно заменяется (интерполируется) более простой функцией (как правило, полиномом 0-го,1- го, 2-го или более высокого порядка), от которой интеграл берется легко. В результате получаются формулы интегрирования, называемые квадратурными, в виде взвешенной суммы ординат подынтегральной функции в отдельных точках xi с весами i :

b

f (x)dx i f (xi ) .

a i

8.1.3. Квадратурные формулы для сетки с равноотстоящими узлами. Квадратурные формулы Ньютона-Котеса

Разобьем отрезок интегрирования [a,b] на n равных отрезков при помощи

то

68

Котеcа. Они не зависят ни от функции, ни от конкретных значений узлов и, следовательно, могут быть вычислены заранее для каждого значения n.

можно получить различные частные случаи квадратурных формул Ньютона-Котеса. Однако на практике не применяют формулы для n 8 , поскольку они становятся вычислительно неустойчивыми.

8.1.4. Частные случаи квадратурных формул Ньютона-Котеса. Простые формулы прямоугольников, трапеций и парабол (Симпсона)

Формулы прямоугольников

Подынтегральную функцию f (x) на отрезке интегрирования [a,b] заменим интерполяционным многочленом нулевого порядка (n 0) , построенным по значению

Это вырожденный случай, когда будет всего один коэффициент Котеса, который, в соответствии со свойствами (7.10), равен единице: H0 1.

В этом случае интеграл функции f (x) на [a,b] вычисляется по приближенной формуле:

Геометрически это означает, что площадь криволинейной трапеции заменяется площадью прямоугольника (Рисунок 8.1), высота которого определяется значением подынтегральной функции в середине интервала. Поэтому такую формулу для вычисления определенного интеграла функции называют формулой средних прямоугольников.

f (x)

f (x)

fa b

2

Рисунок 8.1 – Геометрическая интерпретация метода средних прямоугольников

69