
2 Векторная алгебра
.pdf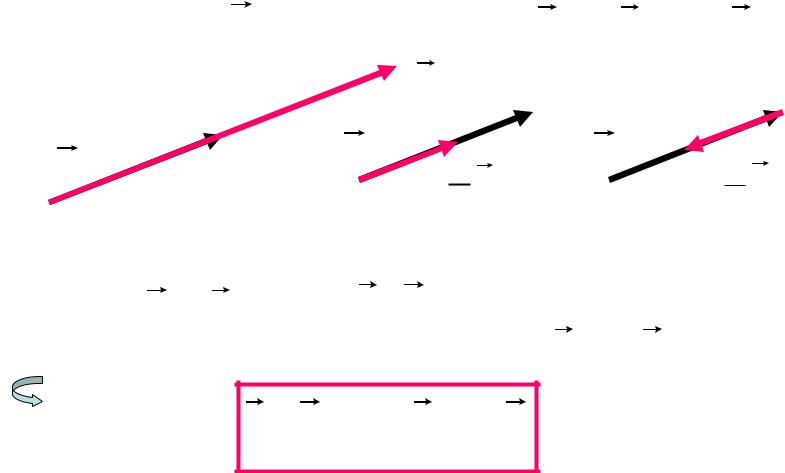
Операции с векторами
• Пример. |
|
|
1 |
|
|
1 |
|
|
Задан вектор a . Построить векторы |
2a, |
a, |
|
a . |
||||
2 |
2 |
|||||||
Построение : |
2a |
|
|
|
|
|||
|
|
|
|
|
|
|
||
a |
a |
|
12 a
a
12 a
•Теорема.
|
a 0 |
b |
|
a |
|
|
Пусть |
. Векторы |
|
и |
|
коллинеарны тогда только тогда, |
|
когда найдется такая постоянная , что |
b a |
|||||
b 
 a b a
a b a
Разложение векторов
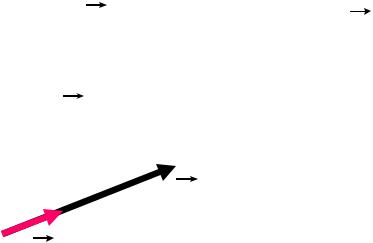
•Разложение векторов по ортам.
•Определение 1.
Ортом вектора a |
o |
называется вектор a , |
имеющий единичную длину и то же направление,
что и вектор a .
a
ao
Разложение векторов
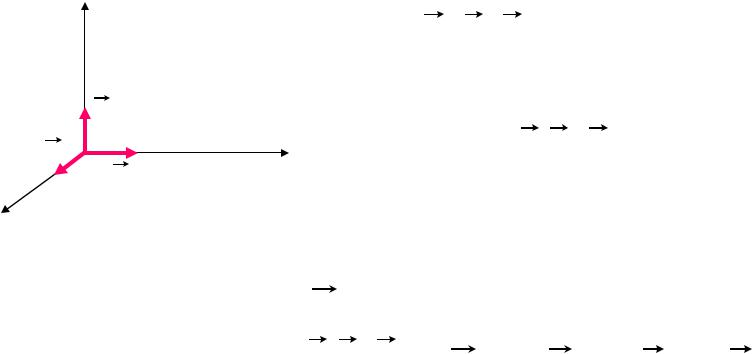
•Рассмотрим прямоугольную систему координат.
z |
|
|
Векторы i , j, k -единичные (орты), |
||
|
|
|
|||
|
|
|
направленные по осям x, y, z (соответственно) |
||
|
k |
|
Определение 2. |
|
|
i 0 |
|
y |
Тройка векторов |
(i, j, k) |
называется |
j |
|
|
|||
|
ортонормированным базисом |
||||
|
|
||||
x |
в пространстве. |
|
• Теорема 3.
В пространстве любой вектор d |
можно |
разложить по |
|
ортонормированному базису (i, |
j, k) : |
|
d xi y j zk |
Такое разложение единственное. |
|
|
|

Разложение векторов
•Определение 3.
Коэффициенты x, y, z разложения
d xi y j zk
называются прямоугольными координатами вектора d : d x, y, z
• Частный случай.
Если вектор d расположен на координатной плоскости хоy, |
|
то разложение будет иметь вид d xi |
y j |
Коэффициенты х, у называются прямоугольными координатами вектора на плоскости : d x, y
Проекции вектора
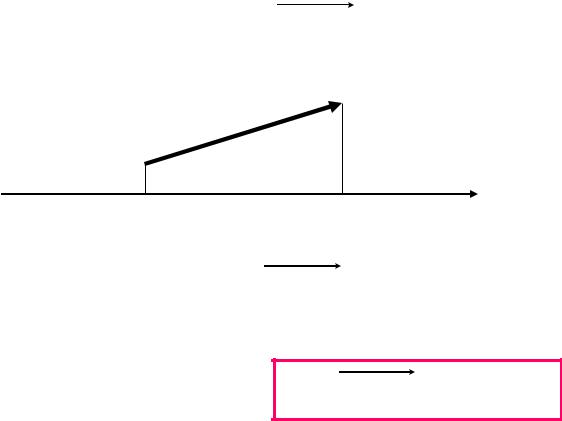
•Рассмотрим вектор M1M 2 и ось
M 2
|
|
M1 |
|
|
|
|
x1 |
x2 |
|
|
|
|
|
|
|||
0 |
|
||||
|
|
|
|
|
|
• Определение. |
|
на ось |
|
||
Проекцией вектора M1M 2 |
называется |
||||
разность проекций концаM 2 |
и началаM1 |
вектора на эту ось; |
|||
Пр M1M 2 x2 x1

Проекции вектора
•В пространстве:
dx, y, z Прх d, Пру d, Прz d
•Следствие.
Если вектор M1M 2 задан двумя точками,
M1 (x1, y1, z1 ) - начало, M2 (x2 , y2 , z2 )- конец,
то
M1M 2 x2 x1, y2 y1, z2 z1
Действия с векторами в координатной форме
• Сумма и разность векторов,
произведение вектора на число. |
|
|
|
|||||||||||||||||||||||||
Пусть |
a x1, y1, z1 и b x2 , y2 , z2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
a b |
x1 x2 , y1 y2 , z1 z2 |
|||||||||||||||||||||||||
|
1. |
|||||||||||||||||||||||||||
|
|
x , y , z |
|
|
|
|||||||||||||||||||||||
|
2. a |
|
|
|
||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
Модуль вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
a |
|
|
|
|
x2 |
y |
2 |
z2 |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
z |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
o |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Орт вектора a |
|
|
|
|
1 |
|
|
, |
|
|
1 |
|
|
|
, |
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Действия с векторами
вкоординатной форме
•Необходимое и достаточное условие коллинеарности векторов, заданных в координатной форме.
Два ненулевых вектора коллинеарны тогда и только тогда, когда соответствующие координаты пропорциональны.
Пусть |
a x1, y1, z1 и b x2 , y2 , z2 |
||||||||||||
|
|||||||||||||
Тогда |
|
a |
|
|
|
b |
x1 |
|
y1 |
|
z1 |
|
|
|
|
||||||||||||
|
|
|
|
x2 |
y2 |
z2 |
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
•Доказательство.
x a b a b zy111
x |
|
|
x1 |
|
y1 |
|
z1 |
||
y2 |
|
|
|
||||||
|
|
|
|||||||
z |
|
2 |
|
x2 |
|
y2 |
|
z2 |
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|||
Скалярное произведение
•Определение.
Скалярным произведением двух векторов
называется число, равное произведению модулей векторов
на косинус угла между ними. |
a |
|
|
|||||
|
|
|
|
|
|
|
b |
|
|
a b |
a |
|
b |
cos |
|||
|
|
|
||||||
|
|
|
|
|
|
Обозначения : a b ab (a,b) |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
•Физический смысл.
|
F |
|
|
M1 |
M 2 |
A F M1M 2
Пусть материальная точка под действием силы F
перемещается из положения M1 в положение M 2 . Работа силы по перемещению материальной точки равна скалярному произведению вектора силы на вектор перемещения.
Скалярное произведение
•Свойства скалярного произведения.
1.a b b a
2.( a) b (a b)
3.a (b c) a b a c
4. a b a Прa b b Прb a
• Следствия из формулы 4 : |
|||||||||||
Пр a |
a |
|
|
|
b |
Прa b |
a |
|
|
b |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
||||||||||
b |
|
b |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
