
RGR_3semestr_Ekonomisty
.pdf
Решение
Дифференцируем заданную функцию по переменной x, учитывая, что
y y x
y3 Cx3 3xy ,
3y2y 3Cx2 3y 3xy ,
откуда
Cx2 y2 y y xy .
Подставляем выражение для Cx2 из последнего равенства в функцию
y3 Cx3 3xy
y3 x y2y y xy 3xy.
Полученное уравнение равносильно исходному. Действительно,
y3 xy2y xy x2y 3xy, y3 xy2 x2 y 2xy,
xy2 x2 y y3 2xy.
Ответ: функция y3 Cx3 3xy является решением дифференциального уравнения xy2 x2 y y3 2xy.
Задача 2.2. Найти общий интеграл дифференциального уравнения первого порядка.
а) Данные к условию задачи, соответствующие вариантам:
1)y sin(x y) sin(x y);
2)3extgydx 1 ex dy 0; cos2 y
3)1 x2 y3 y2 1 x3y ;
4)yx yln y;
5)(1 e2x)y2dy exdx;
6)ex ydx ydy 0;
7)yy ey 0;
x
8)ln cos y dx xcos ydy;
9)2(1 ex)yy ex;
10)y2 y x2 4 y 0;
11)1 (1 y )ey 0;
12)xy 9y2 4;
13)y tg x y 1;
14) dx dy 0;
xy x |
xy 2y |
15)1 y2 x2dx 1 x2 arctg ydy;
16)ey 1 x2 dy 2x 1 ey dx;
17)ye2xdx 1 e2x dy;
18)y2y 1 2x;
19)yy (1 x2) 1 y2;
20)y sin x cosx yln y;
21)(1 ex)yy e2x;
22)y 2
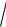 xy ln x;
xy ln x;
30

23) xy ln x y 1; 27) y cos(x y) cos(x y);
24) |
(y x2y)dx (x xy)dy 0; |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||
28) |
1 |
y dx |
|
x |
|
x |
|
y |
1 |
dy; |
|||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
25) |
y |
29) |
xy 2y 2xyy ; |
|
|
|
|
|
|
|
|
||||||||||||
|
(1 y ) 1; |
|
|
|
|
|
|
|
|
||||||||||||||
26) |
y 1 y arccosx; |
|
x |
|
|
|
yy |
|
|
|
0. |
|
|||||||||||
30) |
1 y2 |
1 x2 |
|
||||||||||||||||||||
б) Данные к условию задачи, соответствующие вариантам:
1)2xyy x2 y2 ;
2)x y dx xdy 0;
3) y x y ;
x 2y
4) 2y y2 6 y 4; x2 x
5)xy xtg y y; x
6)xy y2 (2x2 xy)y ;
7)y x 8y ;
8x y
8) y xy x yy ;
9) y x y ;
x 2y
10)y y sin y 0;
xx
11)xyy x2 y2;
12)y y 2;
x
13) |
xy 3yln |
y |
2y; |
|||||||
|
|
|||||||||
|
|
|
y |
|
|
|
x |
|||
|
|
|
|
y |
||||||
|
y ex |
|||||||||
14) |
|
|
; |
|
||||||
|
||||||||||
|
|
2x2 |
|
x |
||||||
|
y |
y2 |
||||||||
15) |
|
|
; |
|||||||
|
|
|||||||||
xy
16)y x 2y ; 2x y
17)ydy x 2y dx 0;
18)y 2x y ; x 2y
19)(y2 3x2)dy 2xydx 0;
20)y x y ;
xy
21)y x 2y ;
2x y
22)xy yln y 0; x
23)x2 y2 xyy ;
24)xyy 2x2 y2 ;
25)y y 1;
x
26)xy y 2xctg y; x
27)y x y;
yx
28)y x 3y ; 3x y
29)y y 2; x
30)x2y x2 xy y2.
31
в) Данные к условию задачи, соответствующие вариантам:
1)xy2 x (y x2y)y 0;
2)3x2 y 4xy2 dx x3 4x2 y 12y3 dy 0;
1 x
3)x y dx y y2 dy 0;
4)2xydy x2 y2 dx;
5)ln ydx x dy 0;
y
6) (1 y ) (1 x )y 0; y x2 x y2
7)e ydx 2y xe y dy 0;
8)x2 y2 xdx ydy xdy ydx;
9)x yex y ex y 0;
10)2xcos2 ydx 2y x2 sin2y dy 0;
11)3x2 2y dx 2x 3 dy 0;
|
x |
|
|
x |
|
x |
||
|
|
|
||||||
12) 2x ey |
dx 1 |
eydy 0; |
||||||
|
||||||||
|
|
|
|
y |
|
|
||
13)ydx 2
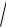 y x dy 0;
y x dy 0;
14)2xdx 3xy2dx 3x2 ydy;
15)x2 y 4 dx x y ey dy 0;
16)y y 3x2 ;
4y x
17)y sin x dx ln y x dy 0;
18)y sin y dx x xcos y dy 0;
19)xdx 2xy2dx 2ydy 2x2 ydy;
20)cos2 ydx 2y xsin2y dy 0;
21)(x2 2y) (2x y3 ey)y 0;
22)1 dx x dy 0;
yy2
23)ex y sin y dx ey x xcos y dy 0;
32

24)y4 x y y 2x3;
25)1 x
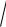 x2 y2 dx 1
x2 y2 dx 1 
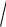 x2 y2 y dy 0;
x2 y2 y dy 0;
26)2xy xey dy x2 y2 ey dx;
27)eydx xey 2y dy 0;
|
|
x dy |
|
y |
|
|
|
|
28) |
|
|
1 dx; |
|||||
|
x2 y2 |
|
||||||
|
|
x2 y2 |
|
|
|
|||
|
|
|
|
|
|
x |
||
29) |
lnx ln y dx y |
|
dy 0; |
|||||
y |
||||||||
|
|
|
|
|
|
|
||
30) 3x2 ydx x3 12y3 dy 0.
Пример 2.2
Найти общий интеграл дифференциального уравнения первого порядка.
а)x2 2yy 1 1.
Решение
Данное уравнение является уравнением с разделяющимися переменными. Разделим обе его части на x2 (x 0, т.к. при подстановке x 0 в уравнение получаем неверное равенство 0 1) и перенесем единицу в правую часть уравнения
2yy 1 |
1 |
, |
|||
x2 |
|||||
|
1 |
|
|
||
2yy |
|
1. |
|||
x2 |
|||||
|
|
|
|||
Учитывая, что y dy, получаем
dx
2y dy 1 1.
dx |
x2 |
|
Умножим обе части уравнения на dx |
1 |
|
|
|
|
2ydy |
|
1 dx. |
|
||
x2 |
|
|
Таким образом, имеем уравнение с разделенными переменными. Вычисляем интегралы каждой части
|
|
|
|
1 |
|
2ydy |
|
|
1 dx, |
||
|
|||||
|
x2 |
|
|||
откуда
33
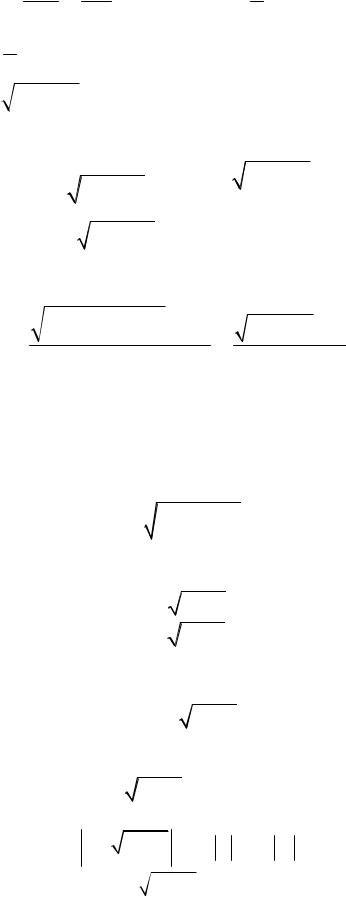
2y2 x 1 x C, y2 1 x C.
2 |
1 |
x |
Ответ: y2 1 x C.
x
б) xdy ydx 
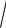 x2 y2dx.
x2 y2dx.
Решение
Перепишем уравнение в следующем виде (x 0)
|
dy |
|
|
|
|
y |
x2 |
y2 |
y |
||||
x |
x2 y2 y, |
||||||||||||
|
|
|
|
|
. |
||||||||
|
|
x |
|
||||||||||
|
dx |
|
|
|
|
|
|
|
|
||||
Правая часть f x, y |
|
|
x2 y2 |
y |
уравнения является однородной функ- |
||||||||
|
|
|
|
|
|||||||||
x
цией по переменным xи y, т.к.
f x, y 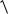
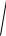 x 2 y 2 y
x 2 y 2 y 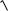
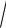 x2 y2 y f x, y .x x
x2 y2 y f x, y .x x
Вследствие этого, само уравнение – однородное. Для решения однородных дифференциальных уравнений применяется замена
t |
|
y |
|
y tx, y |
|
|
|
|
||||||
, |
|
|
||||||||||||
|
t x t, |
|||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
где t t x . Исходя из этого, получаем |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x2 |
|
tx 2 |
|
tx |
|
|||
|
|
|
|
|
|
|
|
|
|
|
, |
|||
t x t |
|
|
x |
|
||||||||||
упростим полученное выражение |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
t, |
||||
|
|
|
|
|
|
|
|
2 |
||||||
|
t x t 1 t |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
1 t . |
|
|
|
|||||||
|
|
|
|
t x |
|
|
|
|||||||
Таким образом, замена позволяет перейти от однородного уравнения к урав-
нению с разделяющимися переменными. |
|
|
|
|
|
|
||||
|
dt |
x |
|
|
|
|
|
|
||
|
1 t2 |
|||||||||
|
|
|
|
|||||||
|
dx |
|
|
|
|
|
|
|||
|
|
|
|
dt |
|
|
dx |
. |
||
|
|
|
|
|
|
|
||||
|
|
1 t2 |
|
|
|
x |
||||
Выполняя почленное интегрирование последнего равенства, получаем
ln t 
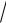 1 t2 ln x ln C
1 t2 ln x ln C
t 
 1 t2 Cx,
1 t2 Cx,
34

возвращаемся к исходной переменной
y
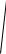 1 y2 Cx, x
1 y2 Cx, x 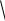 x2
x2
откуда после преобразований имеем
|
|
|
|
y |
Cx2 |
1 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||
|
|
2 |
|
2C |
||||
Ответ: y |
Cx2 |
1 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
||
|
|
|
|
|
||||
2 |
|
2C |
|
|
|
|||
в) yxy 1dx xy ln xdy 0.
Решение
Заданное уравнение относится к уравнениям в полных дифференциалах. Здесь
P x, y yxy 1, |
Q x, y xy 1 ln x |
и |
выполняется |
условие |
||
P x,y |
Q x,y |
|
|
|
|
|
|
|
|
. Действительно, |
|
|
|
|
x |
|
|
|
||
y |
|
|
|
|
||
P x, y xy 1 yxy 1 ln x,
y
Q x, y yxy 1 ln x xy 1 yxy 1 ln x xy 1.x x
Значит, существует функция U x,y C такая, что
dU x, y yxy 1dy xy ln x dx.
Вычислим интегралы от функций P x,y и Q x,y по переменным x и y
соответственно
P x, y dx yxy 1dx y xy 1dx y |
xy |
|
f y xy f y , |
||
y |
|
||||
где функция f y |
|
|
|
|
|
постоянна по отношению к x. |
|
|
|
||
|
|
|
|
xy |
|
Q x, y dy |
xy ln xdy ln x xydy lnx |
|
|
f x xy f x , |
|
|
|
||||
где функция f x |
постоянна по отношению к y. |
ln x |
|||
|
|
|
|||
Таким образом, решение исходного уравнения запишется в виде
xy C.
Ответ: xy C.
35

Задача 2.3. Найти решение задачи Коши заданного дифференциального уравнения.
а) Данные к условию задачи, соответствующие вариантам:
1) xy x2 xy y 0, |
y 1 1 e; |
|||||||||||||||||||||||||||
2) 2xy2 y xy 0, |
|
y 1 0; |
|
|
|
|
|
|
||||||||||||||||||||
3) y y |
|
y |
2 |
|
|
|
|
|
y 0 0; |
|
|
|
|
|
|
|||||||||||||
|
|
|
xy |
, |
|
|
|
|
|
|
|
|||||||||||||||||
4) x2y 2xy 3, |
|
|
y 1 1; |
|
|
|
|
|
|
|||||||||||||||||||
5) x2 1 y 4xy 3, |
|
y 0 0; |
|
|
|
|
||||||||||||||||||||||
6) xy 2y 2x4, |
|
|
y 1 0; |
|
|
|
|
|
|
|||||||||||||||||||
7) y y xy3, |
|
|
y 0 |
|
; |
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
8) |
y ytgx cosx, |
|
y 0 |
0; |
|
|
|
|
|
|
||||||||||||||||||
9)xydy |
|
y2 |
x |
|
dx, |
|
y |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 4; |
|
|
|
|
|
|
||||||||||||||||||
10) |
|
|
|
|
|
|
|
|
|
|
|
2 |
, |
|
|
y |
1 0,5; |
|
|
|
|
|
|
|||||
yx y xy |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
xy 4y 2x2 |
|
|
|
, |
y 1 4; |
|
|
|
|
|
|
||||||||||||||||
11) |
|
|
y |
|
|
|
|
|
|
|||||||||||||||||||
12) |
1 x y y e x, |
|
|
y 0 0; |
|
|
|
|||||||||||||||||||||
13) |
y yctgx cosx, |
|
y 1 0; |
|
|
|
|
|
|
|||||||||||||||||||
14) |
y 2x x2 y , |
|
y 0 0; |
|
|
|
|
|
|
|||||||||||||||||||
15) |
x y y ex, |
|
y 1 0; |
|
|
|
|
|
|
|||||||||||||||||||
16) |
y y ex, |
|
|
y 0 |
1; |
|
|
|
|
|
|
|
|
|
||||||||||||||
17) |
yx x 4y3 |
|
3y2, |
y 2 1; |
|
|
|
|
||||||||||||||||||||
18) |
xy y xe x2 |
|
0, |
|
y 1 |
1 |
|
; |
|
|
|
|||||||||||||||||
|
|
2e |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
19) |
cos ydx x 2cos y sin ydy, |
|
y 0 |
; |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
x2y xy 1 0, |
|
y 1 0; |
|
|
|
4 |
|
||||||||||||||||||||
20) |
|
|
|
|
|
|
|
|||||||||||||||||||||
21) |
y 2y y2ex, |
|
|
y 0 0,5; |
|
|
|
|
|
|
||||||||||||||||||
22) |
2x y dy ydx 4ln ydy, |
y |
0 1; |
|||||||||||||||||||||||||
23) |
y y (1 x)y2, |
|
y 0 1; |
|
|
|
|
|||||||||||||||||||||
24) |
y |
|
|
|
|
|
y |
|
, |
|
|
y 0 1; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3x y2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
36

25) |
1 2xy y y y 1 , |
y 0 1; |
||||||
26) |
y 2xy 2x, |
y 0 e; |
||||||
|
y x y xcosx , |
|
||||||
27) |
y |
|
|
0; |
||||
|
|
|||||||
|
|
|
x |
|
|
2 |
||
28) |
y ytgx |
|
, |
y 0 |
2; |
|||
|
|
|||||||
|
|
cosx |
y 0 1; |
|||||
29) |
y ycosx cosx, |
|||||||
30) |
y x2y x3, |
y 1 |
1. |
|||||
Пример 2.3
Найти решение задачи Коши дифференциального уравнения
xy y y2 ln x, y 1 1.
Решение
Запишем исходное уравнение следующим образом (x 0)
y y y2 ln x. x x
Это уравнение Бернулли. Будем искать его решение в виде
y u x v x ,
тогда
y u x v x u x v x .
Перейдем в уравнении к новым переменным
|
|
|
|
uv |
|
2 |
2 ln x |
||||||||
|
|
|
|
|
u v |
|
|
|
|
|
|||||
|
, |
||||||||||||||
u v uv |
|||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
x |
||||
|
|
|
|
|
v |
|
|
2 |
2 ln x |
||||||
|
|
|
|
|
u v |
|
|
|
|
|
|||||
|
|
. |
|||||||||||||
u v u v |
|
||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
x |
||||
Решение последнего уравнения найдем из системы
|
|
v |
|
|
|
|
|
v |
|
0, |
|
||||
x |
, |
||||||
|
|
|
2 ln x |
||||
|
|
|
|||||
|
|
|
2 |
. |
|||
|
|
|
|
|
|||
|
u v u v |
|
|
||||
x
Первое уравнение системы – уравнение с разделяющимися переменными
v v , dv dx, v 1. x v x x
Подставим значение v во второе уравнение системы и решим его
37

u |
1 |
u2 |
1 |
2 ln x |
|||
|
|
|
|
|
, |
||
x |
|
|
|||||
|
|
x |
|
x |
|||
|
|
du |
|
|
ln x |
xdx, |
||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
u2 |
x3 |
|||||||||||||
|
|
|
|
du |
|
ln x |
dx, |
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
u2 |
|
x2 |
||||||||||
вычислив интегралы от обеих частей равенства, получим |
||||||||||||||||
|
1 |
|
ln x |
|
1 |
C, |
||||||||||
|
|
|
||||||||||||||
|
u |
x x |
||||||||||||||
|
u |
|
|
|
|
x |
||||||||||
|
|
|
. |
|||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
ln x 1 Cx |
||||||||||
Таким образом, общим интегралом уравнения является функция
y |
|
x |
|
|
|
1 |
, |
||||
|
|
|
|
|
|
|
|||||
|
|
lnx 1 Cx x |
|
||||||||
y |
|
|
1 |
|
|
|
|
. |
|
||
|
|
|
|
|
|
||||||
|
|
|
ln x 1 Cx |
|
|||||||
Значение константы C найдем, используя условие y 1 1, |
|||||||||||
1 |
|
1 |
|
, C 0, |
|||||||
|
|
|
|
|
|||||||
|
ln1 1 C 1 |
|
|||||||||
тогда решение задачи Коши |
|
|
|
1 |
|
|
|
|
|||
|
|
|
y |
|
. |
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
ln x 1 |
|
||||||
Ответ: y 1 .
ln x 1
Задача 2.4. Найти функцию спроса qD q p , если известна эластич-
ность ED и объем продаж q q0 при цене p p0 ден.ед.
Данные к условию задачи, соответствующие вариантам с 1 по 15:
1) E |
D |
|
q 100 |
, |
0 q 100, q |
10, p |
30; |
|
|||||||
|
|
q |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
2) |
E |
D |
|
1 |
, |
|
q 3, p 9; |
|
|
|
||
|
|
|
|
|
||||||||
|
|
2 |
|
|
0 |
0 |
|
|
|
|||
3) |
E |
|
|
p |
|
, |
0 p 20, q |
1, p |
|
18; |
||
|
p 20 |
|
||||||||||
|
|
D |
|
|
0 |
|
0 |
|
||||
4) |
ED 2, |
q0 5, p0 2; |
|
|
|
|||||||
38
5) E |
D |
|
q 300 |
, |
0 q 300, q |
20, p |
35; |
|
|||||||
|
|
q |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
6) |
E |
|
|
|
1 |
, |
q |
10, p 8; |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
D |
|
|
|
|
3 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
||||||||
7) |
E |
|
|
|
|
|
|
|
|
|
p |
|
, |
|
|
|
0 p 40, |
q |
60, p |
10; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
D |
|
|
|
|
p 40 |
|
|
0 |
|
|
0 |
|
|
|||||||||||||
8) E |
|
|
|
2 |
, |
q 4, p 8; |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
D |
|
|
|
|
3 |
|
0 |
|
|
0 |
|
|
|
|
|
|
||||||||||
9) |
E |
D |
|
2q 100 |
|
|
, |
0 q 50, q |
|
1, p |
7; |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
0 |
|
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10) |
ED 3, |
q0 |
7, p0 1; |
|
|
|
|
|
|
||||||||||||||||||||
11) |
E |
|
|
|
|
|
|
|
|
|
|
p |
|
, |
0 p 100, |
q |
|
50, p 10; |
|||||||||||
|
|
|
p 100 |
|
|||||||||||||||||||||||||
|
|
|
|
D |
|
|
|
|
|
|
|
0 |
|
|
0 |
||||||||||||||
12) |
E |
D |
|
q 50 |
, |
|
0 q 50, |
q |
29, p |
|
3; |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
0 |
|
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
13) |
E |
|
|
|
|
|
|
|
|
|
|
p |
, |
0 p 15, q |
12, p |
3; |
|||||||||||||
|
|
|
2p 30 |
||||||||||||||||||||||||||
|
|
|
|
D |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|||||||||||||
14) |
E |
D |
|
q 20 |
, |
|
0 q 20, |
q |
6, p |
14; |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2q |
|
|
0 |
|
|
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
15) |
E |
D |
|
3 |
, q |
0 |
8, p 4. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найти функцию предложения qS q p , если известна эластичность ES
и объем продаж q q0 при цене p p0 ден.ед.
Данные к условию задачи, соответствующие вариантам с 16 по 30:
16) |
E |
|
|
1 |
, |
q |
|
8, |
p 16; |
|
|
|
||
|
|
|
|
|
|
|
||||||||
|
|
S |
4 |
|
0 |
|
0 |
|
|
|
||||
17) |
E |
|
|
|
p |
, |
q |
2, p |
6; |
|
|
|||
|
p 20 |
|
|
|||||||||||
|
|
S |
|
|
|
0 |
0 |
|
|
|
||||
18) |
E |
S |
|
q 10 |
, |
q |
11, p |
3; |
|
|
||||
|
|
|
||||||||||||
|
|
|
|
|
q |
|
0 |
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
19) |
E |
|
|
|
p |
, |
p 50, q |
3, p |
|
80; |
||||
|
p 50 |
|
||||||||||||
|
|
S |
|
|
|
|
0 |
|
0 |
|
||||
20) |
ES |
1, |
q0 10, |
p0 5; |
|
|
|
|||||||
39
