Предел числовой последовательности

Если по некоторому закону каждому натуральному числу поставлено в соответствие вполне определенное число , то говорят, что задана числовая последовательность : . Другими словами, числовая последовательность  это функция натурального аргумента: .

Числа называются членами последовательности, а число  общим или -м членом данной последовательности.

Примеры числовых последовательностей:

1) (монотонная, неограниченная);

2) (не монотонная, ограниченная);

3) . Рассмотрим эту числовую последовательность. Изобразим ее точками на числовой оси (рис. 2.5):

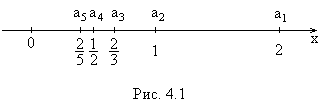
Рис. 2.5

Видно, что члены последовательности с ростом как угодно близко приближаются к нулю. При этом абсолютная величина разности становится все меньше и меньше.

Число называется пределом числовой последовательности , если для любого, даже сколь угодно малого положительного числа , найдется такой (зависящий от ), что для всех членов последовательности с номерами верно неравенство: .Обозначают: или при .

Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Теорема. Если числовая последовательность монотонна и ограничена, то она имеет предел.

Предел функции в бесконечности.

С понятием предела числовой последовательности тесно связано понятие предела функции в бесконечности. Если в первом случае переменная возрастая, принимает лишь целые значения, то во втором случае переменная , изменяясь, принимает любые значения.

Число называется пределом функции при стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа , найдется такое положительное число (зависящее от ), что для всех таких что , верно неравенство: . Предел функции обозначается: или при .

Можно сформулировать понятие предела при стремлении к бесконечности определенного знака, т.е. при и при . В первом случае, основное неравенство: должно выполнятся для всех таких, что , а во втором – для всех таких, что .

Предел функции в точке

Пусть функция задана в некоторой окрестности точки , кроме, быть может, самой точки .

Число называется пределом функции при стремящемся к (или в точке ), если для любого, даже сколько угодно малого положительного числа , найдется такое положительное число (зависящее от ), что для всех , не равных и удовлетворяющих условию , выполняется неравенство . Это предел функции обозначается: или при .

Если при стремлении к переменная принимает лишь значения, меньшие , или наоборот, лишь значения большие , и при этом функция стремится к некоторому числу , то говорят об односторонних пределах функции соответственно слева и справа .

Теорема. Если в некоторой окрестности точки (или при достаточно больших значениях ) функция заключена между двумя функциями и , имеющими одинаковый предел при (или ), то функция имеет тот же предел .

Сформулируем основные теоремы о пределах. Пусть и  функции, для которых существуют пределы при ():,.

1. Функция не может иметь более одного предела.

2. Предел от постоянной величины равен этой величине, т.е. .

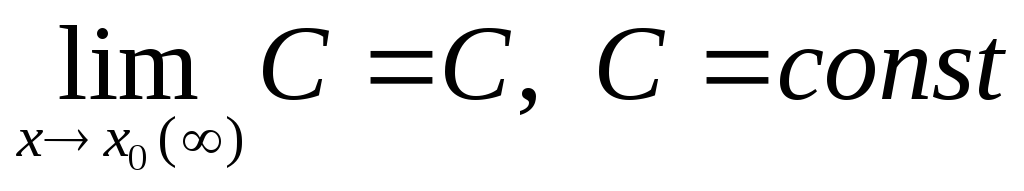3. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е. .

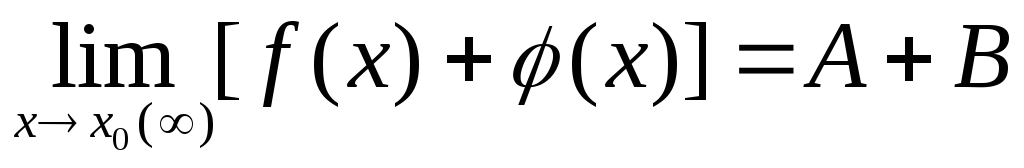4. Предел произведения конечного числа функций равен произведению пределов этих функций, т.е. .

В частности, постоянный множитель можно выносить за знак предела, т.е. .

5. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е. .

6. .

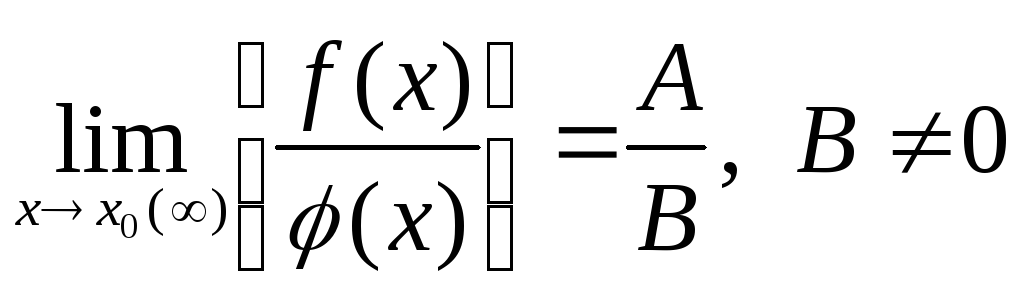7. Если 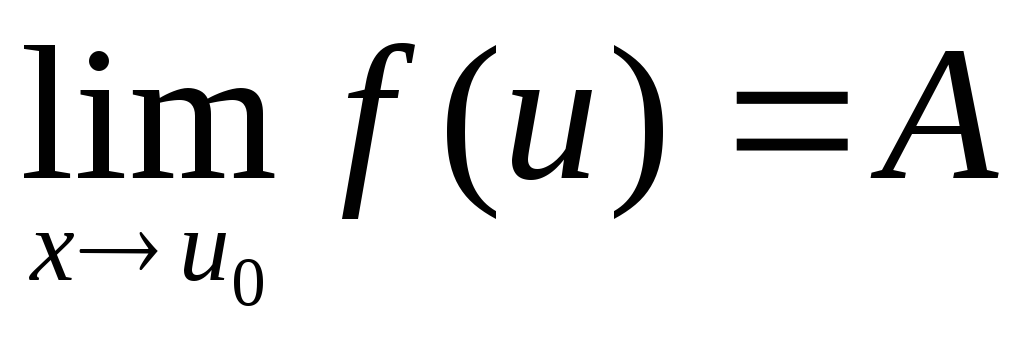, , 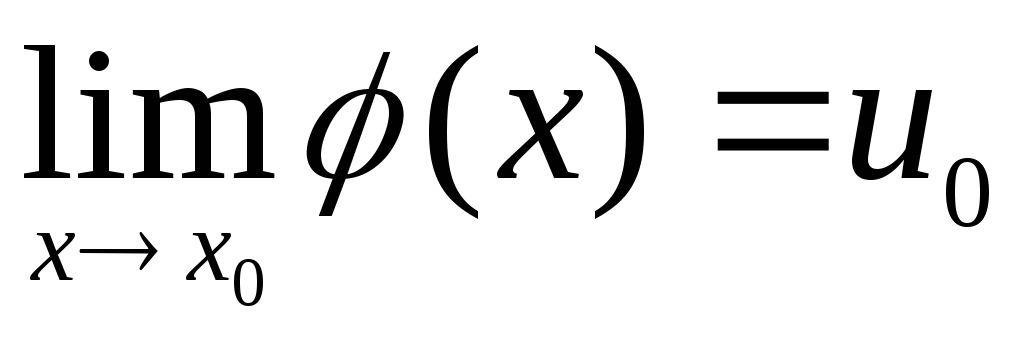то предел сложной функции .

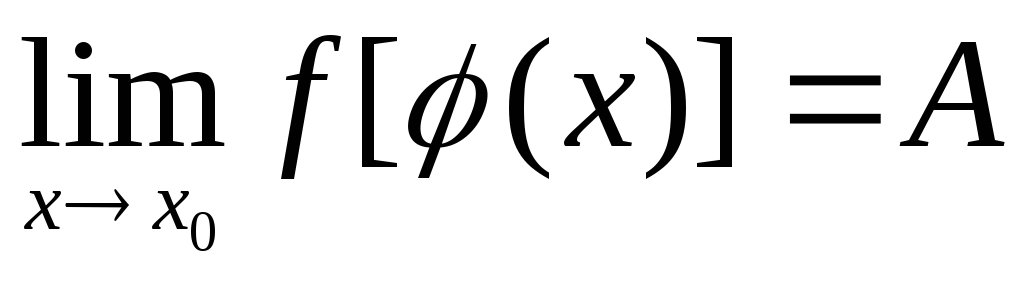8. Если в некоторой окрестности точки 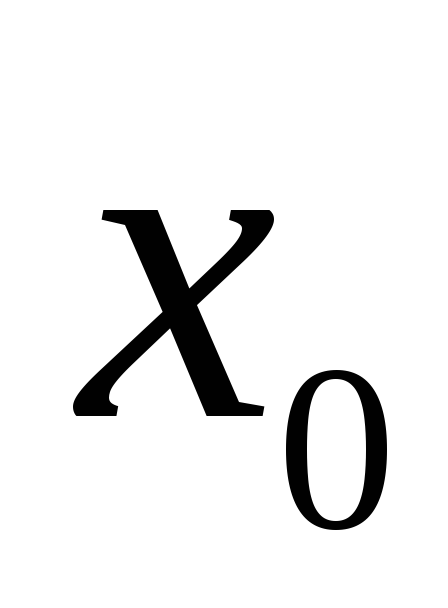(или при достаточно больших 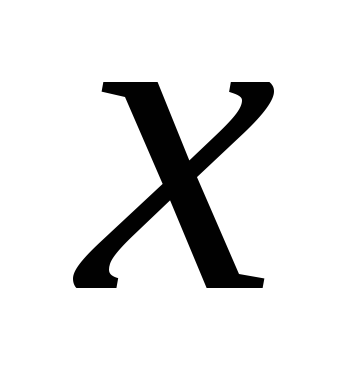) 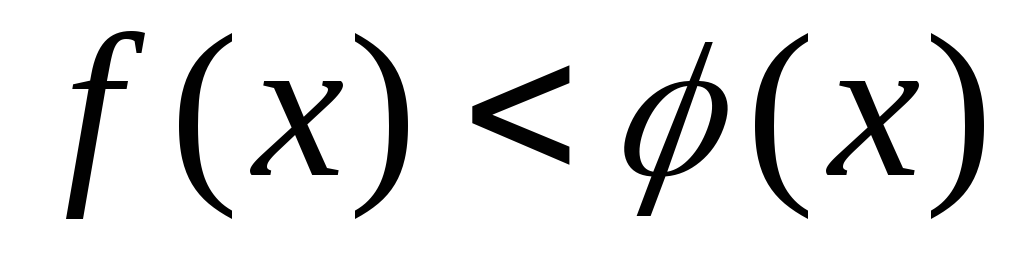, то .
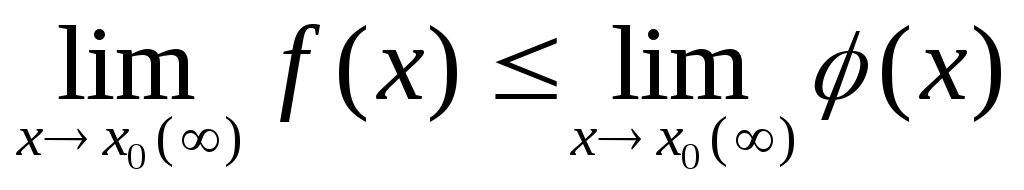