
- •Кафедра высшей математики
- •§ 2. Исследование формы эллипса
- •§ 3. Эксцентриситет эллипса
- •§ 4. Фокальные радиусы эллипса
- •§ 5. Параметрические уравнения эллипса
- •§ 6. Гипербола. Вывод её канонического уравнения
- •2A (24).
- •§ 7. Исследование формы гиперболы
- •§ 8. Эксцентриситет гиперболы
- •§ 9. Фокальные радиусы гиперболы
- •§ 10. Равносторонняя гипербола как график обратной
- •§ 11. Директрисы эллипса и гиперболы
- •§ 12. Парабола
- •§ 13. Общее уравнение для эллипса, параболы и гиперболы
§ 12. Парабола
Определение: Параболой называется множество точек плоскости, равноудалённых от данной точки F, именуемой фокусом, и данной прямой m, именуемой директрисой8.
Пусть
р
– расстояние от фокуса F
до директрисы m.
Ось ОХ декартовой прямоугольной системы
координат выберем так, чтобы она проходила
через фокус F
перпендикулярно прямой m,
а её положительное направление
соответствовало направлению от m
к F.
Начало координат поместим в середине
отрезка BF,
где ( )В
– точка пересечения директрисы с осью
ОХ.NM
= FM
= r,
где r
– расстояние от (
)В
– точка пересечения директрисы с осью
ОХ.NM
= FM
= r,
где r
– расстояние от ( )М
до фокусаF.
)М
до фокусаF.
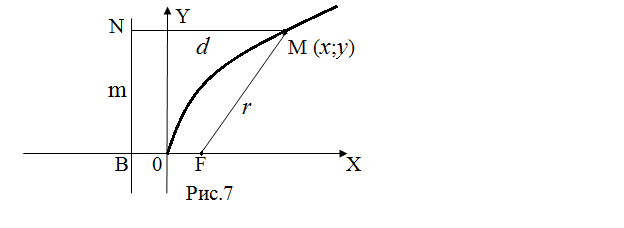
По определению параболы d = r.
Поскольку
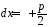 и
и
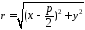 ,
,
То
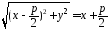 (45).
(45).
Возводя обе части этого уравнения в квадрат и приводя подобные члены, получим
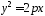 (46).
(46).
Уравнение
(43) называется каноническим уравнением
параболы. Из этого уравнения (с учётом
p
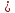 0) следует, чтох
0) следует, чтох
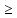 0.
Это
означает, что парабола целиком лежит
справа от оси ОУ. Т. к. у
входит
в уравнение (43) во второй степени, то ось
ОХ является осью симметрии параболы.
0.
Это
означает, что парабола целиком лежит
справа от оси ОУ. Т. к. у
входит
в уравнение (43) во второй степени, то ось
ОХ является осью симметрии параболы.
Уравнение
директрисы, как прямой, параллельной
оси ОУ и проходящей через ( )В,
имеет вид
)В,
имеет вид
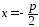 (47).
(47).
§ 13. Общее уравнение для эллипса, параболы и гиперболы
Прямые линии условно можно считать линиями первого порядка. К кривым второго порядка относятся эллипс (частным случаем которого является окружность), гипербола и парабола. Кроме того, в некоторых случаях уравнение второй степени относительно переменных х и у может определять две прямые, точку или мнимое геометрическое место.
Эллипс, параболу и гиперболу открыл в IV веке до н. э. древнегреческий математик Ме́нехм9(др.-греч. Μέναιχμος, латинск. Menaechmus, ок. 380 до н. э. — ок. 320 до н. э.), пересекая разного вида конусы (остроугольный, прямоугольный и тупоугольный) плоскостью, перпендикулярной образующей.
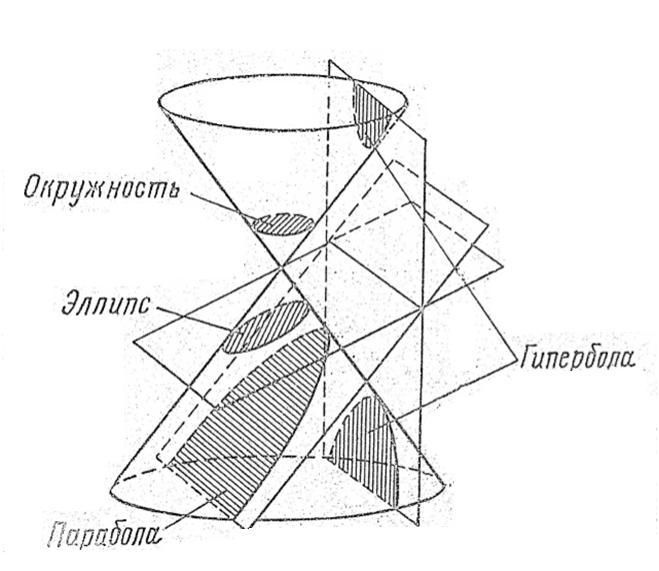
Рис.8
В итоге Менехму удалось свести решение задачи об удвоении куба к нахождению точек пересечения двух парабол.
Более столетия конические сечения не имели собственных названий (указывали лишь способ получения кривых, например, эллипс — «сечение остроугольного конуса»). В истории науки они известны также как «триада Менехма».
Позднее свойства эллипса, параболы и гиперболы изучали многие, в том числе Архимед (др.-греч. Ἀρχιμήδης, 287 до н. э. — 212 до н. э.) и Евклид (др.-греч. Εὐκλείδης, ок. 300 г. до н. э.). Однако наиболее важных результатов добился Аполлоний Пергский (др.-греч. Ἀπολλώνιος ὁ Περγαῖος, 262 до н. э. — 190 до н. э.). Он разработал общую теорию конических сечений, которую изложил в труде «Коника» (отсюда другое бытующее название рассматриваемых кривых — коники). Он же ввёл их современные названия: парабола, гипербола и эллипс.
Долгое время конические сечения не находили применения, пока ими всерьёз не заинтересовались астрономы и физики. Выяснилось, что эти линии встречаются в природе. В соответствии с первым законом Кеплера планеты солнечной системы движутся по эллиптическим орбитам. Кометы, попавшие в солнечную систему из мирового пространства, могут двигаться вокруг Солнца либо по эллипсам, либо по параболам, либо по гиперболам в зависимости от значения скорости, с которой комета приближалась к солнечной системе. Вспомним, наконец, хорошо известные из физики законы Ома10и Бойля-Мариотта11.
Тесная связь конических сечений друг с другом наводит на мысль о возможности описания их единой формулой. Проще всего это достигается при использовании полярной системы координат.
Пусть γ – дуга (рис.9) эллипса, гиперболы или параболы. Если r – расстояние произвольной точки М этой дуги до фокуса F, а d – её расстояние до соответствующей директрисы, то в силу теоремы из §10 и определения параболы
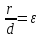 (48).
(48).
Проведём через фокус F прямую, перпендикулярную директрисе m. Точку их пересечения обозначим буквой А, а проекцию точки М на эту прямую – буквой N.
Из
точки F
восставим перпендикуляр к прямой AN
(оси кривой γ)
и обозначим буквой Р
точку её пересечения с дугой γ.
Длину отрезка
РF
обозначим буквой р
(т. е. РF
= р)
и назовём её фокальным параметром линии
γ.


Пусть ρ и φ – полярные координаты точки М в системе координат с полюсом в точке F и полярной осью FN, тогда
r = р (49),
d
= QM = AN = AF + ρ cos
φ
(50).
cos
φ
(50).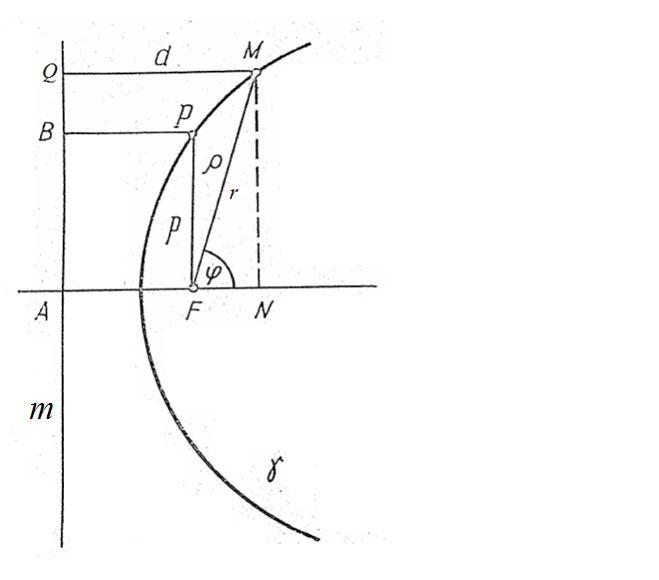
Рис. 9
Равенство (45) выполняется для всех точек линии γ, в том числе и для точки Р, поэтому
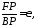

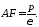
Следовательно,
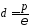 +
ρ
+
ρ cos
φ
(51).
cos
φ
(51).
Подставляя выражения (49) и (51) в равенство (48) и преобразуя его, получаем
Ρ
=
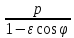 (52).
(52).
Уравнение (52) называется полярным уравнением эллипса, параболы и гиперболы. Следует только отметить, что это уравнение определяет одну из двух ветвей гиперболы.
Для
параболы фокальный параметр совпадает
с параметром
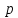 ,
входящим в уравнение (46), а для эллипса
и гиперболы, заданных
,
входящим в уравнение (46), а для эллипса
и гиперболы, заданных
соответственно
уравнениями (22) и (25), он выражается
формулой
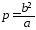
(53).
1Канонический [др.- греч. κανονικως – установленный правилом] – принятый за образец; основанный на законе.
2 Эллипс – от греческ. ελλειψις – недостаток (смысл применения такого термина будет пояснён ниже).
3 Фокус – латинское слово, означающее «очаг». Если в одном из фокусов поместить источник света, то, отражаясь от эллипса, лучи соберутся в другом его фокусе.
4Эксцентриситет – от латинских ex – вне и centrum – центр. Т. е. этот латинский термин в случае дословного перевода звучал бы как «внецентровость ».
5 Пара́метр – [от др.-греческ. παραμετρών – отмеривающий] – переменная величина.
6 Гипе́рбола – от др.-греческ. υπερβολή – избыток, преувеличение.
7 Если в одном из фокусов гиперболы поместить источник света, то после отражения от гиперболы лучи образуют расходящийся пучок (с центром в другом фокусе).
.
8 Директриса – от французского слова directrice, образованного из позднелатинского directrix – направляющая.
9 По преданию Менехм был одним из учителей Александра Македонского.
10 Закон Ома: Сила тока в участке цепи(прямо пропорциональна напряжению и) обратно пропорциональна электрическому сопротивлению данного участка цепи.
11 Закон Бойля-Мариотта: Давление некоторой массы газа, находящегося при постоянной температуре, обратно пропорционально его объёму.
