ГОУ ВПО «Санкт-Петербургский государственный

университет гражданской авиации»

Кафедра высшей математики

ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛА

методическое пособие для самостоятельного изучения

Санкт-Петербург

2015

Составители:

Матусов Ю.А., Смоляр А.Э.

Рецензент:

Заслуженный деятель науки РФ, доктор технических наук,

профессор Попечителев Евгений Парфирович

(Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»)

Пособие рассмотрено и утверждено

на заседании кафедры № 4 высшей математики

Протокол № ….. от ……….. 2015 года

©

СОДЕРЖАНИЕ

стр.

§ 1. Эллипс. Определение и вывод канонического уравнения……...4

§ 2. Исследование формы эллипса…………………………………….6

§ 3. Эксцентриситет эллипса…………….…...…………………….….7

§ 4. Фокальные радиусы эллипса……………………………………...8

§ 5. Параметрические уравнения эллипса……………………………..9

§ 6. Гипербола. Вывод её канонического уравнения……….……….10

§ 7. Исследование формы гиперболы…………………………...……11

§ 8. Эксцентриситет гиперболы…………………………….…….…..13

§ 9. Фокальные радиусы гиперболы……..…….………………….….14

§ 10. Равносторонняя гипербола как график обратной пропорци-

ональной зависимости…………………………………………...14

§ 11. Директрисы эллипса и гиперболы………………………………17

§ 12. Парабола………………………………………….………………19

§ 13. Общее уравнение для эллипса, параболы и гиперболы...….….20

§ 1. Эллипс. Определение и вывод канонического¹ уравнения.

Определение: Эллипсом²называется множество точек плос-кости, для каждой из которых сумма расстояний до двух фиксированных (лежащих в этой же плоскости) точек, именуемых фокусами³, есть величина постоянная, бо́льшая, чем расстояние между фокусами.

Сумму вышеупомянутых расстояний обозначим как 2а.

Обозначим фокусы как F₁ и F₂, а расстояние между ними, именуемое как фокусное расстояние, как 2с (Рис. 1).

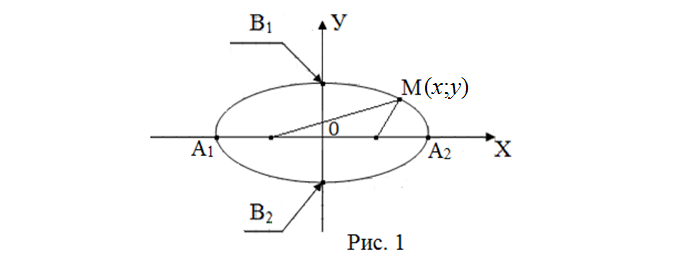
F₁

F₂

Тогда F₁ F₂ = 2с (1),

F₁ М + F₂М = 2а (2).

Из ∆ F₁М F₂ следует, что

F₁ М + F₂ М 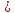F₁ F₂ ,

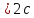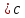т. е. 2а или а (3).

Составим уравнение эллипса, выбрав ось ОХ так, чтобы она проходила через фокусы и имела положительное направление от

F₁ к F₂, а начало координат находилось посредине отрезка F₁F₂.

Тогда координаты некоторых вышеупомянутых точек будут

()F₁(– с; 0), ()F₂ (+ с; 0), ()М(х;у)

На основании теоремы Пифагора

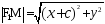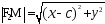и (4).

Подставляя выражения (4) в (2), получим

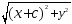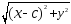+ =2а (5).

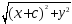= 2а –

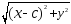
x² + 2cx + c²+y²= 4a² – 4a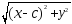+ x²–2cx+ c²+y²

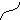
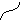
4a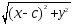= 4a² – 4cx или a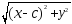= a² – cx

Возводя в квадрат последнее уравнение, находим

а²(x²–2cx+ c²+y²) = а⁴–2а²cx + c²x²

а²x²–2а²cx + а²с² + а²у²= а⁴–2а²cx + c²x²

(а² – c²)x² + а²у ²= а²(a²– c²) (6).

Принимая во внимание (3), вводим обозначение

b²= а² – c² (7).

Тогда выражение (6) принимает вид

b² x² + а²у ² = а²b^2.

или 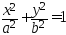(8).

Это выражение называется каноническим уравнением эллипса.