
- •Кафедра высшей математики
- •§ 2. Исследование формы эллипса
- •§ 3. Эксцентриситет эллипса
- •§ 4. Фокальные радиусы эллипса
- •§ 5. Параметрические уравнения эллипса
- •§ 6. Гипербола. Вывод её канонического уравнения
- •2A (24).
- •§ 7. Исследование формы гиперболы
- •§ 8. Эксцентриситет гиперболы
- •§ 9. Фокальные радиусы гиперболы
- •§ 10. Равносторонняя гипербола как график обратной
- •§ 11. Директрисы эллипса и гиперболы
- •§ 12. Парабола
- •§ 13. Общее уравнение для эллипса, параболы и гиперболы
§ 2. Исследование формы эллипса
Из
уравнения (6) следует, что


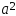 ,
т. е. –
a
,
т. е. –
a
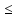 x
x
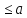 ,
и
,
и

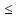
 ,
т. е. – b
,
т. е. – b
 y
y
 b.
b.
Это означает, что эллипс целиком расположен в прямоугольнике с основанием 2а и высотой 2b, а его центр находится в начале координат.
Поскольку в уравнение (8) х и у входят только во второй степени, то эллипс симметричен относительно координатных осей ОУ и ОХ. Для эллипса, описываемого уравнением (8), начало координат является центром симметрии.
Разрешив уравнение (8) относительно у, получим
 (9)
(9)
и
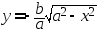 (10).
(10).
Уравнение (9) определяет верхнюю (выше оси ОХ) половину эллипса, а уравнение (10) определяет его нижнюю (ниже оси ОХ) половину.
Точки
пересечения эллипса с координатными
осями называются его вершинами: верхней
– ( )В1(0;b),
нижней – (
)В1(0;b),
нижней – ( )В2(0;–b),
левой –(
)В2(0;–b),
левой –( )А1(–
a;0)
и правой – (
)А1(–
a;0)
и правой – ( )А2(+a;0).
)А2(+a;0).
Отрезки
А1А2
и В1В2
называются осями, а отрезки А1О,
ОВ1,
ОА2,
В2О
– полуосями эллипса. В случае, когда
фокусы расположены на оси ОХ и a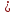 b,
отрезок ОА = a
называют
большой полуосью, а отрезок ОВ = b
–
малой
полуосью.
b,
отрезок ОА = a
называют
большой полуосью, а отрезок ОВ = b
–
малой
полуосью.
При a = b = r уравнение (8) принимает вид
х2 + у2 = r2 (11).
Это соответствует окружности радиуса r с центром в начале координат.
Если
параллельным переносом центр эллипса
(8) переместить в ( )М0(х0;у0),
то его уравнение примет вид
)М0(х0;у0),
то его уравнение примет вид
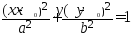 (12).
(12).
Уравнение
окружности радиуса r
с
центром в ( )М0(х0;у0)
будет иметь вид
)М0(х0;у0)
будет иметь вид
 +
+
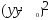 =r2
(13)
=r2
(13)
§ 3. Эксцентриситет эллипса
Определение:
Эксцентриситетом4ε
эллипса называется отно-шение фокусного
расстояния к длине большой оси. В случае
a b
b
эксцентриситет эллипса выражается формулой
ε
=
 (14).
(14).
Для
эллипса c
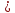 a.
Именно
этим и объясняется использование термина
«недостаток», упомянутого в сноске
2. Для эллипса
a.
Именно
этим и объясняется использование термина
«недостаток», упомянутого в сноске
2. Для эллипса
0
 или
0
или
0 .
Эксцентриситет можно понимать как
мерило сжатости эллипса.
.
Эксцентриситет можно понимать как
мерило сжатости эллипса.
Для
окружности
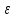 = 0, т. к. с
= 0.
= 0, т. к. с
= 0.
§ 4. Фокальные радиусы эллипса
Определение: Фокальными радиусами точки М, принадлежа-щей эллипсу, называются отрезки, соединяющие эту точку с фокусами.
Из
соотношения (7) имеем
 .
.
Тогда
ε
=

 =
=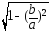 (15).
(15).
Откуда
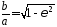 (16).
(16).
Из уравнения (8) найдём у2
у2
=
 (1
–
(1
–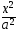 )
)
Тогда
F1M
=
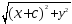 =
=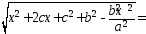
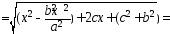
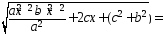


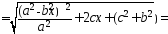 …
…
с
учётом
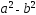 =
=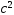 и
и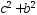 =
=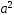 получаем
получаем
…

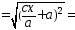
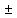
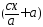 =
=
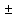

Здесь надо выбирать знак таким образом, чтобы правая часть была положительной.
Таким образом, формула для фокального радиуса F1M имеет вид
F1M
=
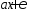 (17).
(17).
Аналогично выводится формула для фокального радиуса F2M
F2M
=
 (18).
(18).
Иногда фокальные радиусы F1M и F2M обозначаются соответст-венно r1 и r2.
§ 5. Параметрические уравнения эллипса

Пусть параметр5t – угол, образуемый отрезком ОМ с осью ОХ (Рис. 2). Тогда параметрические уравнения эллипса можно предста-вить в виде системы
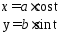 (19).
(19).
В справедливости такого представления проще всего убедиться следующим образом:
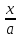 =
cos
t
(20).
=
cos
t
(20). 
 =
sin t
(21).
=
sin t
(21).
Возводя обе части каждого из уравнений (20) и (21) в квадрат и почленно складывая, получим уравнение эллипса
 (22).
(22).
