
- •Кафедра высшей математики
- •§ 2. Исследование формы эллипса
- •§ 3. Эксцентриситет эллипса
- •§ 4. Фокальные радиусы эллипса
- •§ 5. Параметрические уравнения эллипса
- •§ 6. Гипербола. Вывод её канонического уравнения
- •2A (24).
- •§ 7. Исследование формы гиперболы
- •§ 8. Эксцентриситет гиперболы
- •§ 9. Фокальные радиусы гиперболы
- •§ 10. Равносторонняя гипербола как график обратной
- •§ 11. Директрисы эллипса и гиперболы
- •§ 12. Парабола
- •§ 13. Общее уравнение для эллипса, параболы и гиперболы
§ 6. Гипербола. Вывод её канонического уравнения
Определение: Гиперболой6называется множество точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек (фокусов7), лежащих в этой же плоскости, есть величина постоянная.
Обозначим
эту постоянную как 2а,
а расстояние между фокусами F1
и F2
как 2с
(фокусное
расстояние), причём a
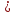 c.
c.
Построим
декартову прямоугольную систему
координат таким образом, чтобы ось ОХ
проходила через фокусы, а её положительное
направление совпадало с направлением
вектора
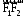 .
Начало координатной системы разместим
в центре отрезка
.
Начало координатной системы разместим
в центре отрезка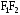 .
Тогда координаты фокусов будут иметь
вид
.
Тогда координаты фокусов будут иметь
вид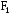 (–с;0)
и
(–с;0)
и
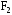 (с;0).
(с;0).
Пусть М (х;у) – произвольная точка гиперболы, тогда


F1
M
– F2
M
= 2a
(23).


F1
M
=
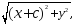 F2
M
=
F2
M
=
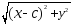




Тогда уравнение гиперболы принимает вид
2A (24).
Знак « – » в правой части выражения (24) получается в том случае, когда в левой части равенства уменьшаемое оказывается меньше вычитаемого.
После упрощений, подобных тем, что делались в §1, получим
каноническое уравнение гиперболы
 (25),
(25),
где
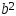
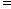 с2–
с2–
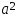 (26).
(26).
§ 7. Исследование формы гиперболы
Из
уравнения (25) следует, что х2
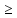 а2.
Это
означает, что в полосе между прямыми х
= – а
и х
= +
а нет
ни одной точки гиперболы.
а2.
Это
означает, что в полосе между прямыми х
= – а
и х
= +
а нет
ни одной точки гиперболы.
Точки, в которых гипербола пересекает действительную ось , называются её вершинами. Если действительная ось гиперболы совпадает с осью ОХ, то это будут точки (– а;0) и (+ а;0).
Поскольку в уравнение (25) переменные х и у входят во второй степени, то гипербола симметрична относительно координатных осей и, следовательно, достаточно изучить её форму в первой четверти, где она определяется уравнением
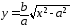 (27).
(27).
При
х
= а
получаем у
= 0. Найдём наклонную асимптоту гиперболы.
Это прямая вида у
=
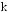
 х
+ q.
Здесь
х
+ q.
Здесь
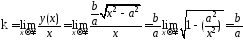 ,
,
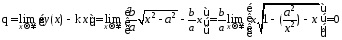
Таким образом, гипербола имеет две наклонные асимптоты
у
=
–
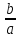 и
у
=
+
и
у
=
+
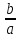 (28).
(28).
Для изображения гиперболы на чертеже сначала построим так называемый основной прямоугольник, центр которого совпадает с началом координат, а стороны равны 2а и 2b и параллельны соответственно координатным осям ОХ и ОУ. Прямые, сопадающие с диагоналями этого прямоугольника, и есть асимптоты гиперболы. Центр их пересечения называется центром гиперболы.
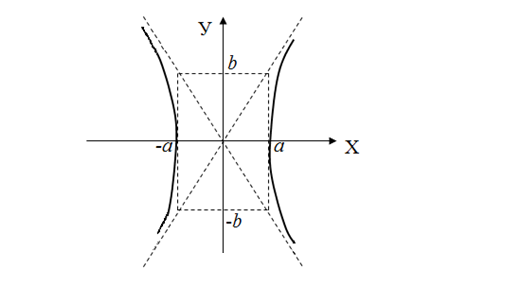
Рис. 4
Координатная ось, пересекающая гиперболу в двух точках, называется действительной осью, а другая координатная ось называется мнимой осью (она не имеет никаких общих точек с гиперболой). Отрезки [-а;+а] и [-b;+b] называются соответственно действительной и мнимой осями гиперболы, а отрезки [0;+а] и [0;+b] называются соответственно действительной и мнимой полуосями. Если а = b, то гипербола называется равносторонней. Её уравнение имеет вид
х2 – у2 = а2 (29).
В этом случае основной прямоугольник гиперболы становится квадратом со стороной 2a.
Гипербола с действительной осью на координатной оси ОУ описывается уравнением
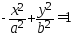 (30).
(30).
Если
параллельным переносом центр гиперболы
(25) переме-стить в ( )
М0(х0;у0),
то её уравнение примет вид
)
М0(х0;у0),
то её уравнение примет вид
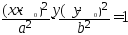 (31).
(31).
