отчёт v2

РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ Факультет физико-математических и естественных наук Кафедра «Систем телекоммуникаций»   Отчёт по курсу

Метод штрафных функций

Студент:	Базырова Б.Н.
Группа:	НП-502
Преподаватель:	Севастьянов А.Л.

Москва

2013

Введение.

В отчёте рассматриваются трёхслойные планарные волноводы. Такой волновод представляет сбой структуру из трёх плоских пластин из диэлектрического материала. Пластины накладываются друг на друга горизонтально. Свет распространяется в среднем слое, отражаясь от границ раздела между слоями. Для того чтобы свет не выходил за пределы среднего слоя на обеих границах должно происходить полное внутренне отражение. Это значит, что коэффициент преломления центральной пластины будет больше чем коэффициент преломления обкладочных слоёв. В математической модели предполагается, что толщины верхнего и нижнего слоёв неограниченны, но это не существенно влияет на ошибку в результатах, так как в реальности подложка и покровный слой всё равно намного больше длины волны.

Теория.

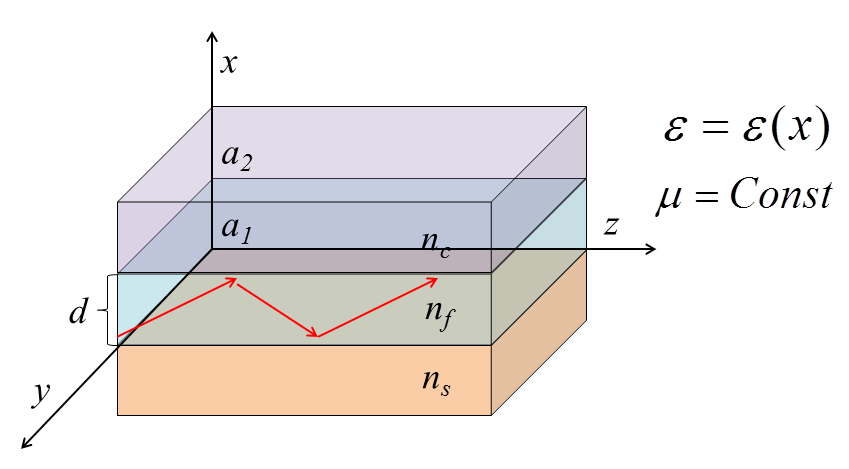
Рисунок 1Схема планарного волновода

На рисунке показана схема плоского волновода , первая граница проходит через точку a1 и вторая через a2 . Как уже , говорилось во введении верхний и нижний слои не ограничены вдоль ос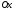и . Каждый слой является однородным , поэтому диэлектрическая проницаемость изменяется только вдоль оси 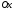: 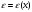. Будем далее рассматривать только диэлектрические среды , соответственно магнитная проницаемость во всей конструкции постоянна и равна проницаемости вакуума: 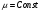. Волна должна идти внутри среднего (волноводного) слоя вдоль оси z .Толщина среднего слоя равна d.

Рассмотрим уравнения Максвелла в диэлектриках:

, , , .

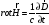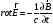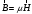Краевые условия для уравнений на границах разделов сред:

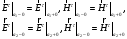
индекс тау означает , что берутся только касательные компоненты, в нашем случае это z и y компоненты:

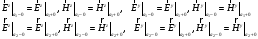
Помимо границ между слоями , необходимы условия на бесконечности , т.е. сверху и снизу:

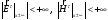
Это условие означает , что в волноводе нет полей с бесконечной энергией .

Далее будем искать решение в рамках модели адиабатических мод. Адиабатические моды это волны , у которых почти вся энергия заключена в некоторой ограниченной области пространства. Таким образом предположим , что общее решение имеет такой вид:

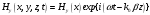
Если взять производные от такого выражения для компонент, то получим:

Поскольку вдоль оси у волна не меняется, то можно считать, что она константа относительно переменной y:

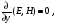
Всё это позволяет нам упростить уравнения Максвелла.

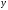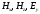Из-за того, что производные по равны нулю, то систему можно разделить на две независимые части, причем в первой системе ненулевыми являются компоненты (TM моды), а во второй (TE моды):

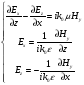
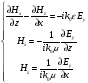
Из этих двух систем можно вывести волновые уравнения.

В поперечных компонентах сначала находится y компонента и затем, через неё выражается z компонента.

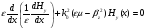
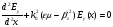
В продольных компонентах наоборот, вначале получают z компоненты

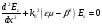
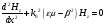
Вводим следующие обозначения

Общие решения:

TM мода в продольных компонентах

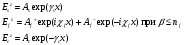
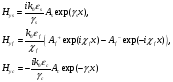
TE мода в поперечных компонентах:

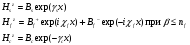
TE мода в поперечных компонентах:

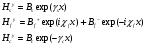
TM мода в поперечных компонентах:

В общих решениях имеются неизвестные амплитудные коэффициенты 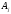и 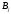. Чтобы определить эти коэффициенты нужны граничные условия.

Если, подставить общее решение в граничные условия, то получатся системы линейных уравнений для амплитудных коэффициентов.

TM мода в продольных компонентах:

TE мода в поперечных компонентах:

TM мода в поперечных компонентах:

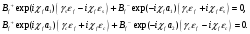
Запишем эти системы в матричном виде. Индексами L (longitudinal) и T (transversal) помечены матрицы в продольных и поперечных координатах.

TE мода в продольных координатах:

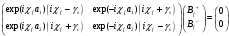
TM мода в продольных координатах:

TE мода в поперечных координатах:

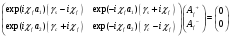
TM мода в поперечных координатах:

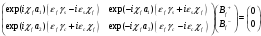
Задача поиска коэффициента фазового замедления.

В системах для амплитудных коэффициентов параметры 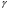и зависят от и от a1,a2. Таким образом, систему можно рассматривать как функцию от коэффициента фазового замедления и толщины:

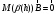
Не нулевые решения этой системы существуют, если определитель системы равен нулю:

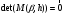
Чтобы найти решение составляется такой функционал:

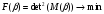
который затем минимизируется при помощи одно из алгоритмов численной оптимизации. Работа велась согласно следующему алгоритму:

• в начале толщина равна нулю

• увеличиваем толщину на некоторый шаг

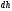
• находим минимум функционала на интервале

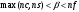
• переходим к шагу два.

Для примера были использованы следующие параметры волновода:

• толщина d=9

• nc=1,458 (кварцевое стекло)

• ns=1,544 (каменная соль)

• nf=1,56 (сахар)

Все значения показателей преломления взяты для волн длиной 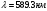и температуре .

В результате получается график, из которого видно что чем больше толщина, тем больше мод может распространяться в волноводе, при этом постепенно моды стремятся к верхней границе:

Рисунок.2 Дисперсионные зависимости для TM мод, H=9, n_c=1, n_s=1.47, n_f=1.51.

Задача нахождения амплитудных коэффициентов.

После решения предыдущей задачи мы получаем набор дисперсионных зависимостей 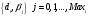при которых система уравнений, представляющая граничные условия, имеет не нулевое решение. Далее нужно подставить какую-либо конкретную пару 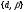, чтобы получить обычную (не функцию) систему уравнений.

Элементы матриц и амплитудные коэффициенты представляют собой комплексные числа, для поиска решений системы вводится функционал следующего вида:

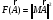
Чтобы обеспечить устойчивость функционал привязывается к решениям, найденным при других значениях параметров волновода. Например, сначала находится решение при толщине равной 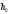, теперь при вычислении функционала для толщины 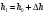нужно, чтобы разница между новым решением и старым уменьшалась при уменьшении величины шага . Таким образом, функционал приводится к следующему виду:

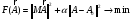
Для минимизации данного функционала было использован алгоритм численной оптимизации: симплекс метод Нелдера-Мида. Этот метод имеет нулевой порядок, т.е. при работе он опирается непосредственно на значения функции и вычисление производных не требуется. Данный алгоритм предназначен для минимизации функций с действительными аргументами, поэтому для программной реализации двумерный вектор комплексных амплитуд заменялся соответствующим четырёхмерным вектором:

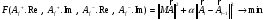
Если подставить найденные амплитудные коэффициенты в формулы для общих решений, то можно получить конкретный вид мод.

Рис..1 Амплитуды 1-й, 2-й,3-й и 4-й TM мод, Н=9, n_c=1,458, n_s=1.56, n_f=1.544 ,a1=0 , a2=9.

Как видно , порядок моды соответствует количеству экстремумов на графике компонент поля. Также хорошо заметно , что поле убывает по мере удаления от центрального слоя

Заключение.

В ходе работы была освоена теория планарных волноводов, решена практическая задача численного моделирования волновода. На основе данных полученных в результате численного эксперимента построены графики , их анализ позволил наглядно ознакомиться с некоторыми закономерностями и явлениями , характерными для мод планарного волновода.

Список литературы

1. Севастьянов А.Л. Компьютерное моделирование полей направляемых мод тонкоплёночной волноводной обобщенной линзы Люнеберга. - М.:РУДН , 2009.

2. Адамс М. Введение в теорию оптических волноводов. – М.: Мир, 1984.

3. Тамир Т. Волноводная оптоэлектроника. – М.: Мир, 1991.

4. А. Снайдер, Дж. Лав Теория оптических волноводов. – М.: Радио и связь, 1987.

5. Хансперджер Р. Интегральная оптика. – М.: Мир, 1985.

6. Терлецкий Я.П., Рыбаков Ю.П. Электродинамика. – М.: Высшая школа, 1990.

7. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. – М.: Наука, 1982.