сборникДУ- ЕП

УДК 517.91 (075.8) ББК 161.61 я73

С 896

Рецензент:

доцент кафедры «Высшая математика» Дальневосточного государственного университета путей сообщения,

кандидат физико-математических наук

Г. А. Ушакова

Суляндзига, Е. П.

Задания по дифференциальным уравнениям : сборник задач

С896 [Текст] / Е. П. Суляндзига. – Хабаровск: Изд-во ДВГУПС, 2007. – 44 с.

Сборник задач соответствует государственному образовательному стандарту подготовки специалистов направления 010501 специальности 01050165 «Прикладная математика и информатика».

Сборник содержит задания по всем темам курса – в первую часть включены задания для электронного промежуточного и итогового тестирования студентов. Вторая часть содержит задачи для самостоятельного решения по темам – дифференциальные уравнения первого порядка, разрешимые в квадратурах, дифференциальные уравнения высших порядков, случаи понижения порядка. Третья часть пособия включает задания для проведения контроля по итогам семестра.

Сборник может быть использован при проведении аудиторных занятий, для выполнения самостоятельных, расчетно-графических работ, при подготовке к тестированию. Рассмотрены примеры решения задач.

Предназначено для студентов 2 курса дневной формы обучения.

УДК 517.91 (075.8) ББК 161.61 я73

ГОУ ВПО «Дальневосточный государственный университет путей сообщения» (ДВГУПС), 2007

2

ВВЕДЕНИЕ

Изучение теории обыкновенных дифференциальных уравнений включает в себя постановку задачи – дифференциальное уравнение с начальными условиями; разрешение вопросов существования и единственности решения; построение аналитического точного или приближенного решений исходной задачи.

В современных исследованиях актуальны задачи на стыке различных наук: биофизика, социальная экология, биокибернетика и др., а построенные математические модели часто содержат обыкновенные дифференциальные уравнения. Поэтому представляется важной способность участвующего в исследовании специалиста-математика рассмотреть вопросы существования решения, найти решение задачи подходящим способом, оценить устойчивость решения, т. е. применить теорию обыкновенных дифференциальных уравнений.

Дисциплина "Дифференциальные уравнения" обучает студентов основным методам решения обыкновенных дифференциальных уравнений и использованию при математическом моделировании физических, биологических и других процессов. Основными задачами дисциплины являются изучение вопросов существования и единственности решений различных типов дифференциальных уравнений и систем дифференциальных уравнений, нахождения точных решений уравнений 1-го порядка, интегрируемых в квадратурах, уравнений n-го порядка, допускающих понижения порядка, линейных дифференциальных уравнений с постоянными и переменными коэффициентами; изучение основных методов доказательства существования и единственности решений начально-краевых задач для указанных уравнений, вопросов устойчивости решений по Ляпунову, ознакомление с приближенными методами решения указанных уравнений и обучение студентов применению теории дифференциальных уравнений в прикладных задачах.

Данный сборник содержит различные задания по всем темам курса. Приведены задания, составленные автором и входящие в различные контрольные и самостоятельные работы, включенные в компьютерный тест итогового контроля.

3

ЗАДАНИЯ ДЛЯ ПРОВЕДЕНИЯ ТЕСТИРОВАНИЯ

Задание 1. Определить вид изоклин для уравнения, указать правильный ответ из группы

параболы

прямые

гиперболы концентрические окружности концентрические эллипсы

1)y'(y2 + 1) + x = 0

2)xy'+y = 0

3)y'= y2 + x2

4)xy'+y = 0

5)y'= y − x2 + 4x

6)y'(y2 + y) + x −1= 0

7)(1− x2 )y'−y2 = 0

8)y'= (y −1)2 + (x + 1)2

9)xy'+3y = 4

10)y'= y − x2

Задание 2. Укажите общее решение дифференциального уравнения

y"+y = 0

y = c1COS x + c2 SIN x

y = c1e− x + c2ex

y = c1 + c2e− x

y = c1e− x

Задание 3. Сколько решений имеет дифференциальное уравнение

y"+y'+2y = 0?

единственное решение

два решения

не имеет решений

бесконечное множество решений

4

Задание 4. Укажите общее решение дифференциального уравнения y"+y'= 0

y = c1COS x + c2 SIN x

y = c1e−x + c2ex

y = c1 + c2e−x

y = c1e−x

Задание 5. Для решения неоднородного линейного дифференциального уравнения надо:

1:записать соответствующее однородное уравнение и к нему характеристическое,

2:по виду корней характеристического уравнения определить общее решение однородного уравнения,

3:по правой части подобрать частное решение неоднородного,

4:общее решение неоднородного есть сумма общего однородного и частного неоднородного.

решения соответствующего однородного уравнения и частного решения исходного неоднородного?

Задание 7. Верно ли утверждение:

общее решение линейного однородного уравнения n-го порядка есть линейная комбинация функций фундаментальной системы решений.

верно

не верно

формулировка не точна.

Задание 8. Если корни характеристического уравнения комплексносопряженные, то общее решение уравнения содержит

синусы и косинусы

только синусы

только слагаемые вида eλx .

Задание 9. Найти решение уравнения y"−4y'+4y = 0

y(x) = c1e2x + c2 xe2x

5

y(x) = c1e2x + c2

y = c1 + c2e− x

Задание 10. Укажите решение уравнения y"'+8y = 0

y(x) = c1e−2x + ex (с2 COS 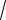3x + c3 SIN 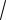3x)

y(x) = e−2x (c1x2 + c2 x + c3 )

нет правильного ответа

Задание 11. Для линейного дифференциального уравнения 2-го порядка в зависимости от корней характеристического уравнения решение имеет вид – поставьте в соответствие пары

Задание 12. Отметьте правильный ответ.

Линейное дифференциальное уравнение в частных производных первого порядка можно решить

методом Лагранжа

при помощи первых интегралов

методом Эйлера.

уравнения будет вида

y = Ax3 + Bx2 + Cx

y = Ax2

y = Ax2 + Bx + C

y = xex (ACOS x + BSIN x)

y = ex (AxCOS x + BSIN x)x2

частное решение уравнения будет вида

y = ex (ACOS x + BSIN x)x + ex x2 (Cx + D)

y = x2ex (ACOS x + BSIN x + Cx)

нет правильного ответа

y = ex (ACOS x + BSIN x + C)x2

y(n) + a1y(n−1) +...+ ai y(n−i) +...+ an y = f (x) имеет:

бесконечное множество решений

не имеет решений

единственное решение

n решений

Задание 17. Определите тип уравнения y"+2y = xCOS x

линейное однородное

уравнение Клеро

уравнение Эйлера

линейное неоднородное

dy dx

Задание 18. Найдите общий интеграл уравнения y + 1 = x2 + 1

LN y +1 = arctgx + c

LN y = LN(x2 +1) + c

Задание 19. Найдите общий интеграл уравнения y'= 1 .

3x + 1

y = 1LN(3x + 1) + c

3

y = LN(3x +1) + c

7

1 e2y = tgx + c

2

2e2y = tgx + c

e2y = 1 + c

COS x

Задание 21. Данное уравнение можно разрешить при помощи подстановки

y'= p(x) y'= p(y) y'= yz

y = tx

1)y"+xy'= 0

2)y"−(y + 1)2 y'= 0

3)(x + 1)(ex − y") = y'

4)y"y'= 1

5)y"y'= x

6)x(y"−LN x) + y'= 0

7)y"= (y + 1)y'

Задание 22. Найти решение уравнения xy"= y'

y(x) = c1x2 + c2

2

y(x) = 1 x2 + c

2

y(x) = cx2

1 y'

Задание 23. Найти решение уравнения 2 y"= x2 −1

8

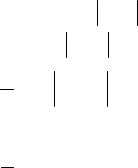
y(x) = c1x − 2c1 LN x +1 + c2y(x) = c1x + LN x + 1

y(x) = 1c1 LN x2 −1 + c2

2

Задание 24. Найти решение уравнения (x + 1)y"−2y'= 0

y(x) = 1(x +1)3 + c

3

y = c1(x + 1)3 + c2

Задание 25. Сколько решений имеет дифференциальное уравнение

y'+y = x

бесконечное множество

единственное решение

не имеет решений

два решения

Задание 26. Определите порядок дифференциального уравнения

(y'+ y)2 − yy'= 0

Задание 27. Поставьте в соответствие уравнению его решение

Задание 28. Укажите верный ответ

Сколько решений имеет дифференциальное уравнение n-го порядка

бесконечное множество решений

единственное решение

n решений

(n+1) решение

Задание 29. Укажите правильный ответ Сколько решений имеет задача Коши

не имеет решений

единственное решение

n решений

бесконечное множество решений

9

Задание 30. Определитель Вронского фундаментальной системы решений

равен 1,

всегда равен 0,

не существует,

не равен нулю.

Задание 31. Отметьте правильный ответ. Теорема Коши утверждает, что

дифференциальное уравнение имеет бесконечное множество ре-

шений

задача Коши имеет n решений

задача Коши имеет единственное решение

через каждую точку фазовой плоскости проходит по крайней мере одно решение.

Задание 32. Отметьте правильный ответ. Решения системы с постоянными коэффициентами будут периодическими, если

корни характеристического уравнения матрицы системы будут комплексными,

матрица системы будет симметрической,

порядок системы больше двух.

Задание 33. Отметьте правильный ответ. Нормальная cистема ОДУ имеет

бесконечное множество решений,

n решений,

единственное решение.

Задание 34. Верно ли утверждение: характеристическое уравнение системы ОДУ есть характеристическое уравнение матрицы системы

это зависит от корней характеристического уравнения,

не верно,

верно.

Задание 35. Отметьте правильный ответ. Линейные дифференциальные уравнения в частных производных первого порядка можно решить

методом Лагранжа,

при помощи первых интегралов,

методом Эйлера.

Задание 36. Укажите правильный ответ.

10