
сборникДУ- ЕП
.pdf
Функция f (x, y), определенная в области G, удовлетворяет в G условию Липшица относительно y, если
существует число L > 0, такое что для любых двух точек (x,y), (x,z) из G выполнено неравенство f (x, y) − f (x,z) ≤ L y − z ;
существует число L > 0, такое что f (x, y) ≤ L;
существует число L > 0, такое что f (x, y) ≤ L y .
Задание 37. Верно ли, что
y'= f (x, y),
решение задачи Коши y(x0 ) = y0 геометрически можно интерпрети-
ровать как нахождение интегральной кривой, имеющей в каждой точке заданный угловой коэффициент, и проходящей через точку (x0 , y0 ).
Задание 38. Укажите правильный ответ. Сколько решений имеет задача y'= x2 + 2x −1, y(0) = 1
бесконечное множество,единственное решение,n решений,
(n-1) решение.
Задание 39. Укажите правильный ответ. Сколько решений имеет зада-
ча Коши y"= xSIN x, y(0) = 0, y'(0) = 1 ?
два решения,одно решение,
не имеет решений,бесконечное множество решений.
Задание 40. Выберите верное утверждение:
через особую точку ОДУ y'= f (x, y) либо не проходит ни одна интегральная кривая, либо проходит по крайней мере две интегральные кривые;
через особую точку ОДУ y'= f (x, y) проходит единственная интегральная кривая;
через особую точку ОДУ y'= f (x, y) проходит бесконечное множество интегральных кривых;
нет верного утверждения.
Задание 41. Выберите верное утверждение
11

Решение задачи Коши |
y'= f (x, y), y(x0 ) = y0 |
непрерывно зависит |
от начальных данных, если выполнены условия теоремы Коши. |
||
Решение задачи Коши |
y'= f (x, y), y(x0 ) = y0 |
непрерывно зависит |
от начальных данных. |
|
|
Решение задачи Коши |
y'= f (x, y), y(x0 ) = y0 |
непрерывно зависит |
от начальных данных, если f (x0 , y0 ) ≤ x0 − y0 .
Задание 42. Укажите правильный ответ При помощи метода Лагранжа можно получить
единственное решение уравнения,
общее решение уравнения,
n решений уравнения.
Задание 43. В теоремах Ляпунова рассматриваются вопросы
существования решений,
единственности решений,
устойчивости решений.
Задание 44. Отметьте правильный ответ. Уравнение y"+ y = 1 мож-
SIN x
но решить
методом Бернулли,
методом Лагранжа,
при помощи подстановки y = tx,
методом подбора частного решения по правой части.
Задание 45. Решение y = g(t) системы dy = f (t, y)асимптотически dt
устойчиво по Ляпунову, если
оно устойчиво и выполнено условие LIM
t→+∞

 y(t) − g(t)
y(t) − g(t)
 = 0;
= 0;
ε > 0, 
 y(t) − g(t)
y(t) − g(t)
 < ε;
< ε;
оно устойчиво и LIM g(t) = g(t0 ).
t→+∞
Задание 46. Будет ли устойчиво тривиальное решение системы
x'= 2y − x,
= + 4
y' y x
да,
12

нет,
устойчивость не определяется.
Задание 47. Будет ли особая точка уравнения y'= 4x + 5y устойчива? x + 2y
Задание 48. Уравнение Эйлера можно решить при помощи подстановки
y = tx
y = p(x)
y'= p(y)
y = eτ
Задание 49. Сколько линейно независимых первых интегралов имеет
уравнение y ∂z + xy |
∂z = xy |
|
|
|
∂x |
∂y |
|
|
|
Задание 50. Поставьте в соответствие пары |
||||
Задача Коши |
|
y"− |
y' |
= x, y(0) = 0, y'(0) = 1 |
|
|
|||
|
|
|
||
|
|
|
x |
|
линейное ДУ 2-го порядка |
y"−y = SIN x |
|||
Уравнение с разделяющимися пе- |
y'= y COS x |
|||
ременными |
|
y"= SIN x, y(π ) = 0, y'(0) = 1 |
||
|
|
|||
Задание 51. Определите тип уравнения первого порядка с разделяющимися переменными однородное линейное
в полных дифференциалах
x − y 1) y'= x + y
2) (2x + y)dx + (x − ey )dx = 0
3) y'= x + y y
4) y2dx + 2xydy = 0
Задание 52. Поставьте в соответствие пары:
13

дифференциальное уравнение первого порядка – его тип
y'= f (x)g(y) |
с разделяющимися переменными |
||
y'= |
a1x + b1y |
|
однородное уравнение |
|
|
||
a2x + b2 y |
|
||
|
|
||
y'+p(x)y = q(x) |
линейное уравнение |
||
y'= y2 + x2 |
|
||
Задание 53. Укажите подстановку, при помощи которой решается урав-
нение y'− y = x
x
y = tx
y = uv
y = p(x)
Задание 54. Поставьте в соответствие уравнению способ решения
y'= f (x) g(y) |
непосредственное интегрирование |
||
y'= |
a1x + b1y |
|
подстановка y = tx |
|
|
||
a2x + b2 y |
|
||
|
|
||
y'+p(x)y = q(x) |
подстановка y = uv |
||
y"+ay'+c = 0 |
|
||
Задание 55. Метод Бернулли основан на использовании подстановки
y = tx
y = uv
y = zm
Задание 56. Укажите правильный ответ. Какое из уравнений является уравнением в полных дифференциалах
2xydx + (x2 − y2 )dy = 0
(3x − y2 )dy − ydx = 0
Задание 57. Укажите правильный ответ. Какое из уравнений можно решить подстановкой y = tx
xy'−2y = 2x4
(y + x)2 = y'
14

y'= x+ y x− 2y
Задание 58. Какое из уравнений является линейным уравнением первого порядка
y'= yx+ x
(x + 1)y'= x
xdy = 
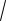 x −1y2dx
x −1y2dx
Задание 59. Методом Бернулли можно найти решение
уравнения в полных дифференциалах
линейного уравнения первого порядка
однородного уравнения
Задание 60. Какое из уравнений является уравнением с разделяющимися переменными?
y'= yCOS x
y'x + y = y2 COS x
x(y + x)dy − exdx = 0
Задание 61. Какое из уравнений является уравнением в полных дифференциалах?
y2dx + 2xydy = 0
ydx + 2xdy = 0
2y3dx − 3xy2dy = 0
Задание 62. Какое из уравнений является уравнением Бернулли?
xy'−2y2/3 = 2x4 y
(y + x)2 = y'−2xy
dy + (4x − x2 )dx = 0
Задание 63. Какое из уравнений является линейным уравнением первого порядка?
dy − (x + y)dx = 0
y'= y2x + x
(x + 1)y'= x
15
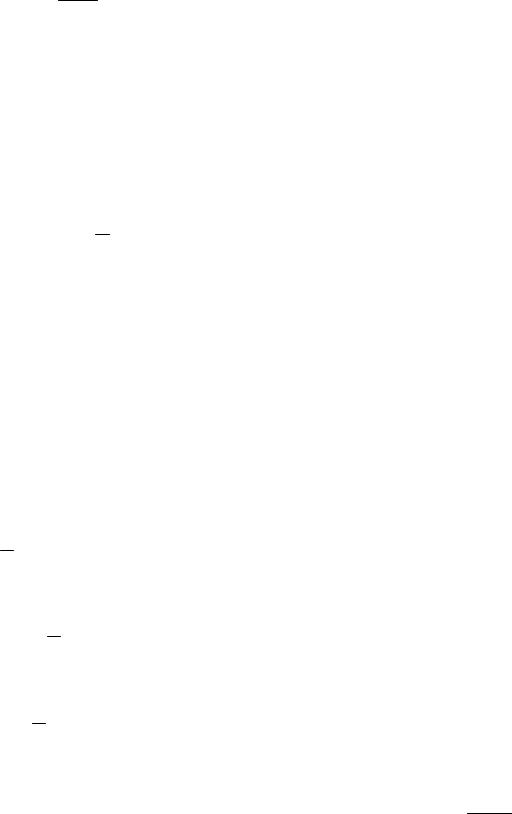
xdy = 
 x −1y2dx
x −1y2dx
Задание 64. Сколько решений имеет задача { y"−y'= 2x + 1, y(0) = 0}
бесконечное множество,
одно решение,
два решения,
не имеет решений.
Задание 65. Выберите правильный ответ
Уравнение y'+ y = x2 + 1 нужно решать подстановкой x
y = u v
y = tx
y = p(x)
Задание 66. Определите тип уравнения первого порядка
–с разделяющимися переменными
–однородное
–приводящееся к однородному
–линейное
–уравнение Бернулли
1)(x +1)dy + ydx = (x +1)dx
2)y'x3 = yx2 − y2
3)
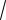 xydy − (y2 −1)dx = 0
xydy − (y2 −1)dx = 0
4)(x + 2y)dx − xdy = 0
5)dy = (COS x + y)dx
6)y'= y
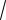 x − y2 / 3
x − y2 / 3
7)dy + COS ydx = xSIN ydy
y 2
8)y'= +1
x
9)(x +1)dy + ydx = (x +1)exdx
x + y
Задание 67. Сколько особых точек имеет уравнение y'= x − y ?
16
Дифференциальные уравнения первого порядка, разрешенные в квадратурах
Пример 1. Решить ОДУ первого порядка y′ −1= COS(y + x).
Решение. Это дифференциальное уравнение первого порядка приводящееся подстановкой x + y = z к уравнению с разделяющимися переменными. Произведем замену переменных, пусть x + y = z . Тогда z′ = 1+ y′, y′ = z′ −1. Подставив в уравнение получим дифференциальное уравнение первого порядка с разделяющимися переменными.
z′ − 2 = COS z,
|
|
|
|
|
z′ |
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
COS z + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Переменные разделены. Проинтегрируем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
∫ |
|
|
|
dz |
|
|
= ∫dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
COS z + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решим |
|
|
интеграл |
|
|
dz |
|
|
|
с |
|
|
помощью |
универсальной |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
∫ COS z + |
2 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тригонометрической подстановки, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
2dt(1+ t2 ) |
|
|
|
2dt |
|
|
|
|
dt |
|
|
1 |
|
|
t |
||||||||
|
∫ |
|
|
|
|
|
|
|
= ∫ |
(1+ t |
|
|
)(1− t |
|
|
|
|
) |
= ∫ |
|
|
|
= 2∫ |
|
|
|
= 2 |
|
|
|
arctg |
|
|
|
|
||||
|
|
COS z + 2 |
2 |
2 |
+ 2 + 2t |
2 |
3 + t |
2 |
|
|
+ t |
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|||||||||||||||||||||
Общим решением дифференциального уравнения будет выражение: |
|||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
tg |
z |
|
|
|
− x = C, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
arctg |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Вернемся к исходным переменным
2 |
|
|
y + x |
|
|
|
|
arctg tg |
|
|
|
|
|
|
|
|
|
||
3 |
|
|
2 |
|
При делении на
3 = x + C .
(COS z + 2) мог быть потерян корень (COS z + 2) = 0, но
COS z [−1;1] следовательно корни потеряны не были.
Ответ: общий интеграл |
2 |
|
|
y + x |
|
|
|
= x + C . |
|
|
3 |
||||||||
|
|
|
arctg tg |
|
|
||||
|
|
|
|
||||||
|
3 |
|
|
2 |
|
|
|
|
|
Пример 2. Решить ОДУ первого порядка x2(dy − dx)= (x + y)ydx. Решение. Проверим, что дифференциальное уравнение – однородное
первого порядка, приведем к виду
y′ = xy + y2 + x2 , x2
применим подстановку y = tx, уравнение примет вид:
17

t′x + t = x2t + x2t2 + x2 = t + t2 +1, x2
t′x = t2 +1.
Разделим переменные и проинтегрируем:
∫ t2dt+ 1 = ∫ dxx ,
arctg(t)= LN x + C где t = y . x
При делении на |
1 |
было потеряно решение |
x = 0, – особое решение. |
|||
|
x2 |
|||||
|
|
|
|
|
|
|
y |
= LN x + C,x = 0. |
|
||||
Ответ: arctg |
|
|
|
|||
|
|
|||||
x |
|
|
|
|
||
Пример 3. Решить y'= SIN y + x .
COS y
Решение. Перепишем уравнение COS yy'= SIN y + x и заметим, что
COS yy'= (SIN y)'. Сделаем замену переменной z(x) = SIN(y(x)), получаем z'−z = x - линейное уравнение первого порядка относительно функции
z. Решим методом Лагранжа, а именно,
запишем соответствующее однородное уравнение
z'−z = 0,
dz = dx, z
LN z = x + c ,
zодн = cex .
Будем искать решение неоднородного уравнения в виде zн = c(x)ex . Чтобы найти неизвестную функцию c(x), подставим
решение в уравнение
c'(x)ex + c(x)ex − c(x)ex = x , c'(x) = xe−x ,
c(x) = ∫ xe−xdx = −(x +1)e−x + c1.
Получено решение z = (− (x +1)e−x + c1)ex = c1ex − x −1. Ответ: y = ARCSIN(c1ex − x −1).
18
Самостоятельная работа № 1
Вариант 1
y'−yctgx = 2xSIN x, |
|
|
||||||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
) = 0 |
|
|
|
|
|
|
|
|
|
||
y( |
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
yLN2 y + y' |
|
|
|
|
|
|||||||
|
2x + 1 |
= 0 |
|
|||||||||
(x + 4y)y'= 2x + 3y |
|
|
||||||||||
y'− |
y |
= |
(x2 |
+ y |
2) |
(x |
− y) |
2 |
||||
x |
|
x4 |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
Вариант 2 |
|
|
|
|
|
|
|
|
|
|||
y'= 2x−2y |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
y'+ yCOS x |
= |
|
|
SIN 2x, |
|
|||||||
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
y(0) = 0
y
xy'= y − xex
y = (SIN x + COS x −1)y'−1
Вариант 3
(1+ ex )y'= yex
|
|
2xy |
|
|
|
2x |
2 |
|
|
||||
y'+ |
|
|
= |
|
|
, |
|||||||
x2 |
|
+ |
|
|
x2 + |
|
|||||||
|
|
|
1 |
1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
y(0) = |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3 |
|
|
|
|
|
|
|
||
y'= |
x2 |
+ xy − y2 |
|
|
|
|
|||||||
|
x |
2 − 2xy |
|
|
|
||||||||
|
|
|
|
|
|||||||||
y'= yCOS x + COS3 x
Вариант 4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dx |
|
+ |
|
|
|
|
|
dy |
|
|
|
= 0 |
||||||||
|
x(y −1) |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
y(x2 + 2) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x, |
|
|
|||||
y'+ ytgx = COS |
|
|
|
|
|||||||||||||||||
|
π) = |
0,5 |
|
|
|
|
|
|
|
|
|
|
|||||||||
y( |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x2(y'−12) = y(y + 8x) |
||||||||||||||||||||
|
y'+ |
|
xy |
|
= x2 −1 |
|
|
|
|
||||||||||||
|
x + 1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вариант 5 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2x + 2y2x + y' |
|
|
2 − x2 = 0 |
||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
y'− |
|
|
|
= x |
|
|
+ 2x, |
|
|
||||||||||||
x + 2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y(−1) = |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
xdy = (y + |
|
|
|
|
|
|||||||||||||||
|
xy)dx |
|
|
||||||||||||||||||
|
x(y' − tg |
y |
) = x + y |
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||
Вариант 6 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y3 − 3xy2 + x2 y |
= x |
2 y' |
||||||||||||||||||
|
|
|
y − x |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y'− 2y = x3ex2 +1 x
x(2x2 y − y)3dx − dy = 0 3
{y'= 
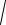 x + y, y(−1) = 1}
x + y, y(−1) = 1}
19
Вариант 7
(y + 1)COS xdx + 
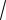 SIN x + 2dy = 0
SIN x + 2dy = 0
|
|
6x |
2 |
y |
2 |
|
||
|
= |
|
|
+ y, y(4) = 0 |
||||
2xy' |
|
|
|
|
|
|||
x2 |
+ 4x |
|||||||
|
|
|
||||||
|
|
|
|
|
|
|
||
y'(x2 + 2xy) = 3y2+5xy |
||||||||
y'= 1+ |
|
|
|
|||||
|
2x + y |
|
||||||
Вариант 8
1
(x2 +1)2 dy + x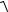
 2 − y2dx = 0
2 − y2dx = 0
xy'+ y = x3
2
|
|
|
|
x + y |
||
xy'−y |
= (x + y)LN |
|
|
|||
|
||||||
|
|
|
|
|
x |
|
y'− |
|
|
y |
= arctgx earctgx |
||
|
|
|
||||
|
x |
2 + 1 |
|
|
||
Вариант 9
x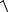
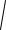 y2 + 5dx + y
y2 + 5dx + y
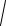 4 − x2dy = 0
4 − x2dy = 0
|
y |
π |
|
y'+ |
|
= SIN x, y( |
) = 1 |
|
|||
|
x |
2 |
|
y |
|
xy'− y = xtg |
|
x
(y2 − y + 4)dx − (SIN x + 2)dy = 0
Вариант 10
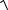
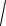 4 − x2 y'+xy2 + x = 0
4 − x2 y'+xy2 + x = 0
y'− |
2xy |
|
= |
2x2 |
|
|
x2 + 1 |
x2 + 1 |
|||||
|
|
|||||
20
y − xy' |
= |
(x + y)2 |
||
x − y |
|
xy |
||
|
||||
y2 + x2 y'= xyy'
Вариант 11
y(4 + ex )dy − exdx = 0
|
2x − 5 |
|
|
y'− |
|
y = 5, y(2) = 4 |
|
x2 |
|||
|
|
2y'= |
y2 |
+ 6 |
y |
+ 3 |
|
|||||||||||
x2 |
|
|
|
|||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|||||
(x + 1)y'= y + (x + 1)3 ex |
||||||||||||||||
Вариант 12 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1+ yy' |
|
1− x |
2 |
|
= 0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
1− y |
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
y |
|
|
|
|
x + |
1 |
|
|
|
x |
|
|
|||
y'+ |
|
|
= |
|
|
|
|
|
e |
|
, y(1) |
= e |
||||
|
|
|
|
|
|
|
|
|||||||||
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
y'(x − y) = x + y
y'(x2 − 4)− 4xy = (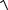
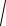 x2 − 4)3
x2 − 4)3
Вариант 13 |
|
|
||
|
y |
|
LN x |
|
y'+ |
|
= −2 |
|
, y(1) = 1 |
|
|
|||
|
x |
|
x |
|
(e2x + 5)dy + ye2xdx = 0 2x(x − y)y'= x2 + 2xy − y2 y'= xex+1(y2 + 1)(y2 −1)
