1. Одномерная цепочка одинаковых атомов, находящихся на одинаковом расстоянии -(Линейная цепочка).

Пусть нами возбуждена бегущая по цепочке плоская волна

Плоскую волну, распространяющуюся в однородном

твердом теле вдоль оси х, можно записать в виде

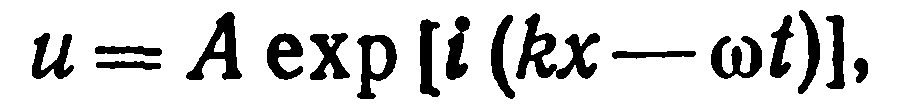(1)

[ Напоминаю, что здесь записана гармоническая функции, т.к. по формуле Муавра exp(ix)=cosx+isinx, отсюда Re(u)=Acos(kx-𝜔t)]

где u — смещение, А — амплитуда, k — волновой вектор и 𝜔 — угловая частота.

Рассмотрим линейную цепочку одинаковых атомов (рис. 1), имеющих массу m и расположенных на расстоянии а один от другого.

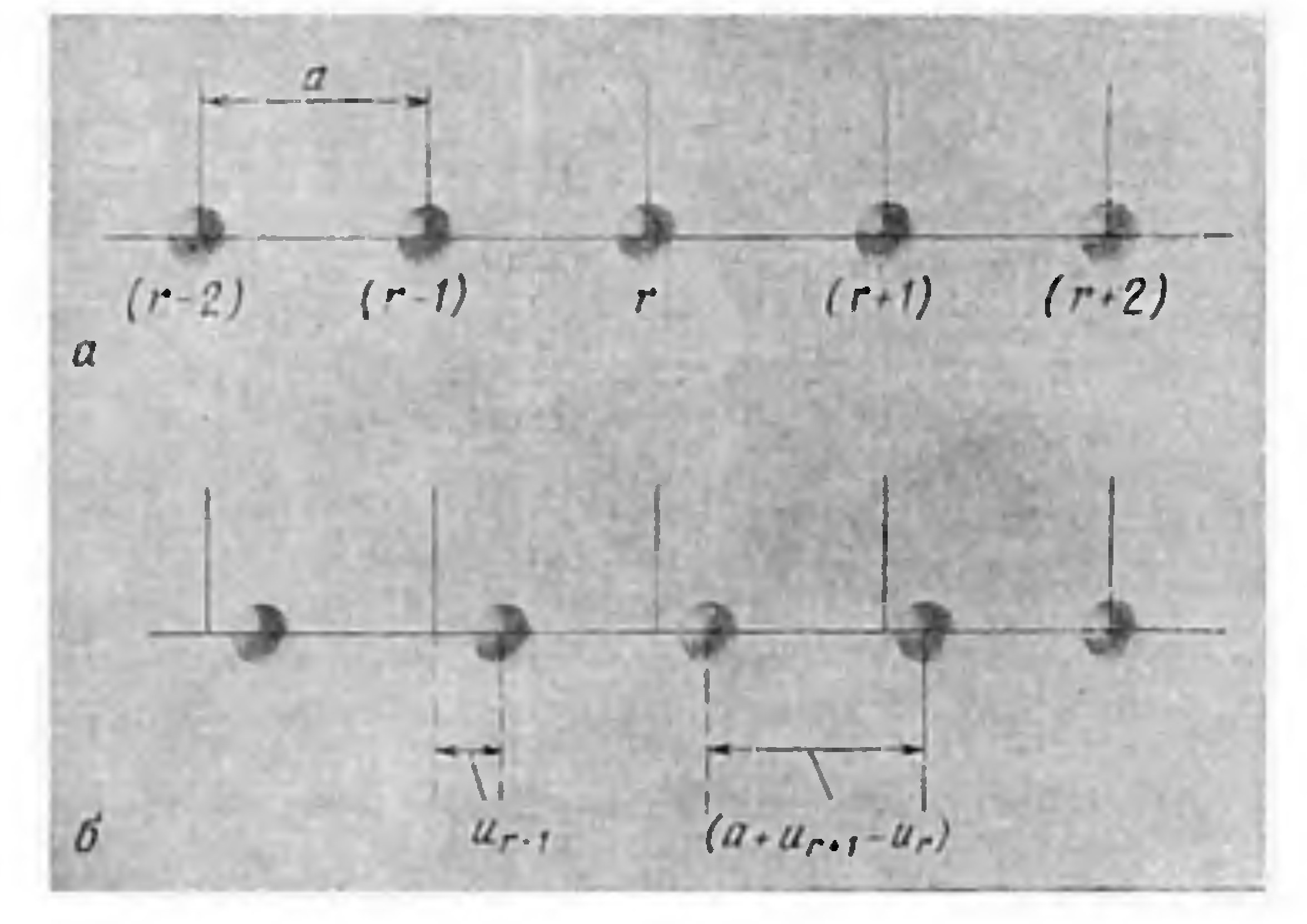
Рис. 1. Пять соседних атомов в линейной одноатомной решетке, а — атомы находятся в равновесных положениях; б — атомы смещены вследствие прохождения продольной волны.

Для этой последовательности атомов создаваемое волной (1) смещение u имеет смысл только в точках расположения атомов и не имеет смысла в

промежуточных точках х. Таким образом, смещение r-го атома запишется в виде

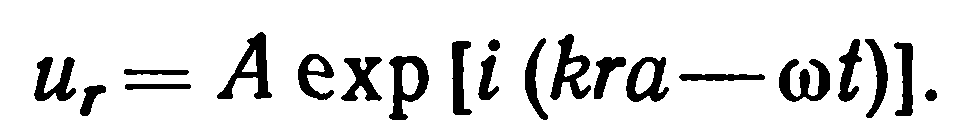(2)

Дифференцируя это выражение два раза, получаем ускорение r-го атома:

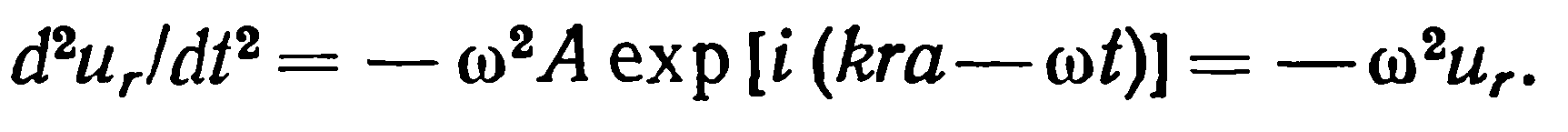(3)

Согласно второму закону Ньютона, возвращающую силу,

действующую на r-й атом, можно записать в виде

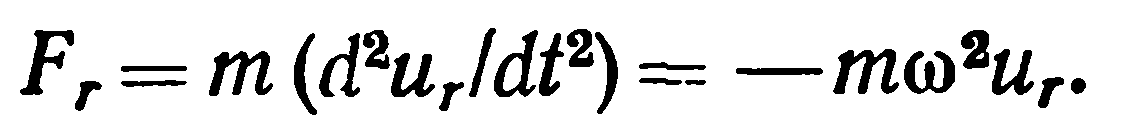(4)

Для установления закона дисперсии, т.е. связи между 𝜔 и k эту возвращающую силу необходимо выразить через силовую постоянную, характеризующую смещения атомов в кристаллической решетке.

Для этого представим нашу линейную цепочку в виде шариков, связанных пружинками. В этой модели возникающая при растяжении или сжатии возвращающая сила, действующая на атом, линейно зависит от расстояния до ближайших соседей (с коэффициентом пропорциональности μ) и не зависит от

положения более удаленных атомов. Следовательно, возвращающая сила подчиняется закону Гука

На первый взгляд кажется, что эта модель не может соответствовать сложному квантово- механическому характеру взаимодействия между атомами. Однако следует напомнить, что для большинства твердых тел в случае малых деформаций выполняется закон Гука, устанавливающий линейную связь между смещением и приложенной силой.

В приближении закона Гука сила, действующая на r-й

атом на рис. 1, имеет вид

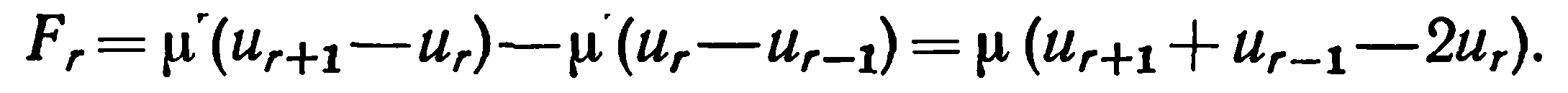(5)

Сравнивая этот результат с выражением (4)

(4) ,

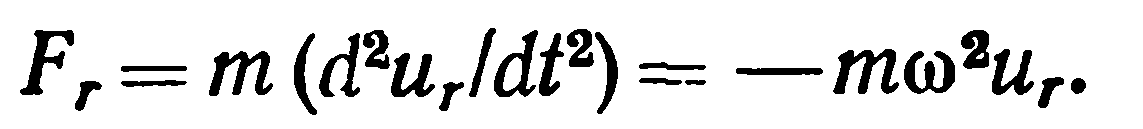получаем

(6)

Подставляя сюда выражение (2) для смещения,

(2)

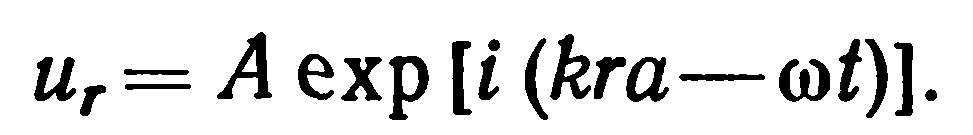
последнюю формулу можно переписать в виде

Дисперсионное уравнение – форма 1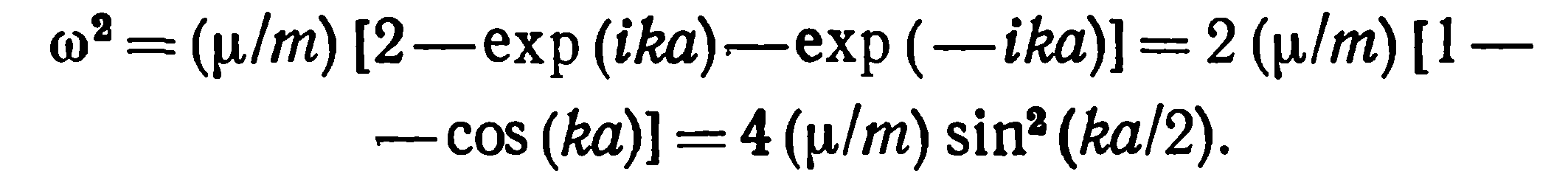 (7)

Таким образом, дисперсионное уравнение для продольных волн, которые могут распространяться в линейной одноатомной цепочке, при учете взаимодействия только с ближайшими соседями запишется как

Дисперсионное уравнение – форма 2 (См. рис 2)

(8)

Знаки плюс и минус в выражении (8) отвечают волнам, распространяющимся в противоположных направлениях.

Движение в любой точке решетки является периодическим во времени.

На рис. 2 представлена дисперсионная кривая, построенная в соответствии с уравнением (8). Эта кривая качественно подобна той, которую можно получить с учетом зависимости возвращающей силы от расстояний не только до ближайших, но и до более удаленных соседей (см. задачу Л7-1).

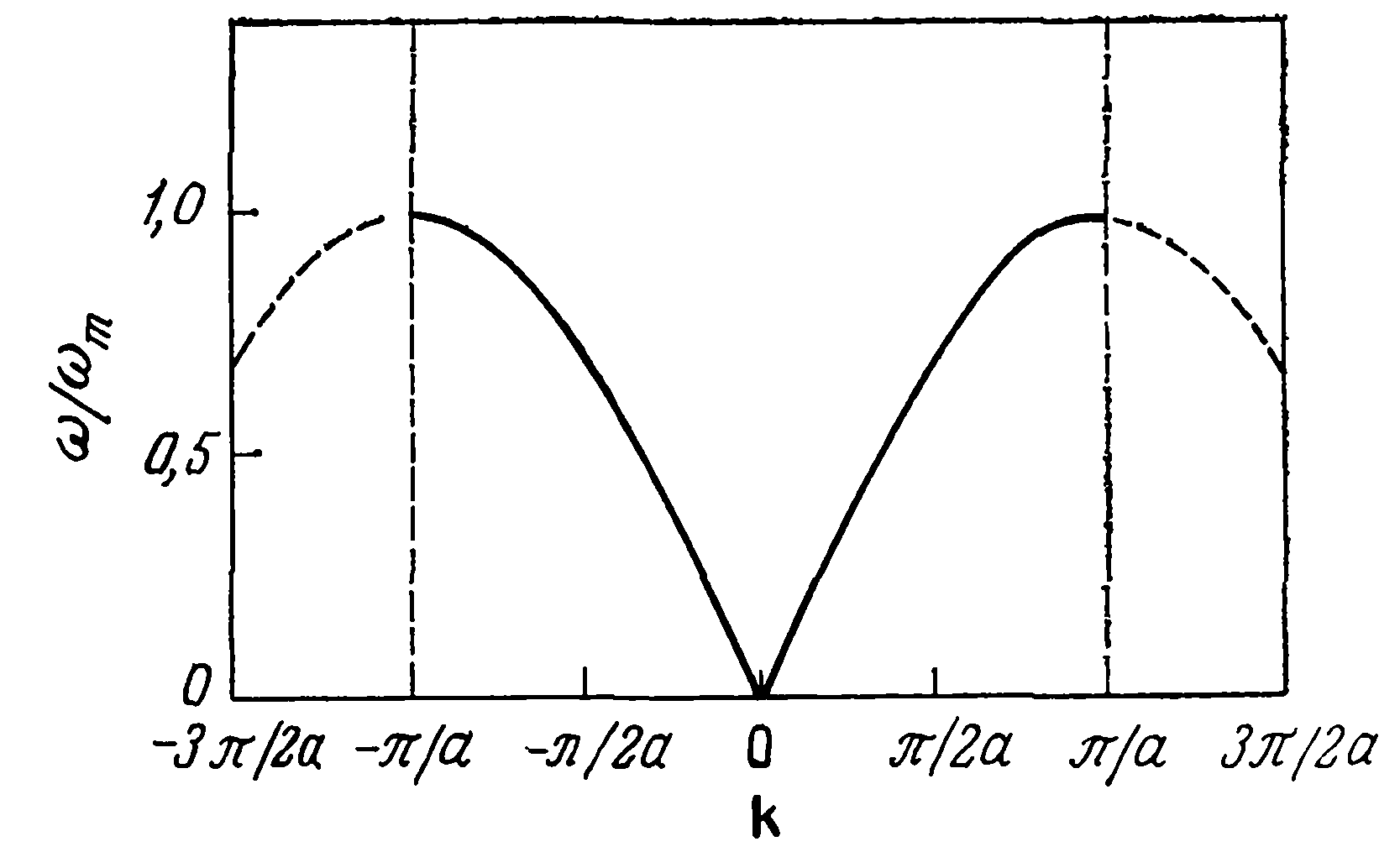
Рис. 2. Дисперсионная кривая для продольной волны, распространяющейся в линейной моноатомной решетке; получена с учетом взаимодействия только ближайших соседей [выражение (8)]. Область k-пространства, для которой |к|<<π/а, образует первую зону Бриллюэна. По оси ординат отложена безразмерная частота в единицах максимальной угловой частоты, для которой величина к вещественна, 𝜔_m=(2μ/m)²=2(v₀/a). Поскольку звуковые волны в кристаллах распространяются, как правило, со скоростью v₀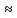5000 м/с, эта максимальная угловая частота имеет порядок 𝜔_m ~10¹⁴ рад/с. ЭТО ДИСПЕРСИОННАЯ КРИВАЯ ДЛЯ АКУСТИЧЕСКИХ ФОНОНОВ

АКУСТИЧЕСКИЕ ФОНОНЫ – одноатомная цепочка

В качестве независимой переменной на рис. 2 вместо длины волны λ выбран волновой вектор к, что более удобно (как мы увидим при разборе других задач физики твердого тела).

Область малых к соответствует спектральному диапазону (длинных волн, для которых вполне годится макроскопическое рассмотрение распространения звуковых волн. В случае когда kа<<1, мы можем положить sin (ka/2)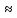ka/2. При этом соотношение между угловой частотой и волновым вектором принимает вид

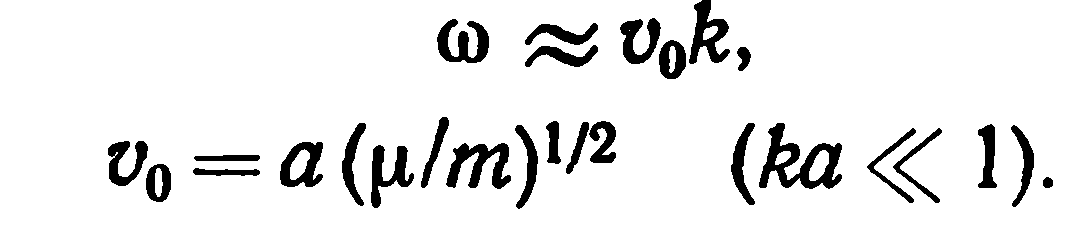(9)

В области больших длин волн или низких частот дисперсия отсутствует, так что фазовая скорость 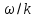и групповая скорость совпадают и оказываются равными скорости звука v₀. Скорость v₀=(μ/m)^1/2 , полученная для больших длин волн согласно этой модели, полностью согласуется с выражением для непрерывной упругой среды.

Даже в рамках грубой одномерной модели, если известна скорость v₀ обычных звуковых волн в твердом теле, то можно рассчитать межатомный коэффициент жесткости по формуле

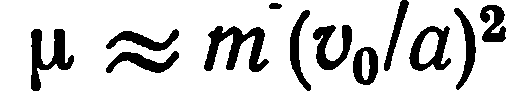(9.1)

Рассматриваемое на данном этапе низкочастотное приближение справедливо вплоть до частот 10¹² Гц или около того, что перекрывает так называемый акустический» или «ультразвуковой» диапазон частот, в котором работают экспериментальные монохроматические установки.

Однако из рис. 2 мы видим, что по мере перехода ко все более коротким волнам величина 𝜔 достигает предельного значения 𝜔_m

𝜔_m=(2μ/m)²=2(v₀/a), когда . (10)

Промежуточные частоты

В области промежуточных частот наблюдается сильная дисперсия скорости звука. В общем виде зависимости фазовой и групповой скоростей от к имеют вид соответственно

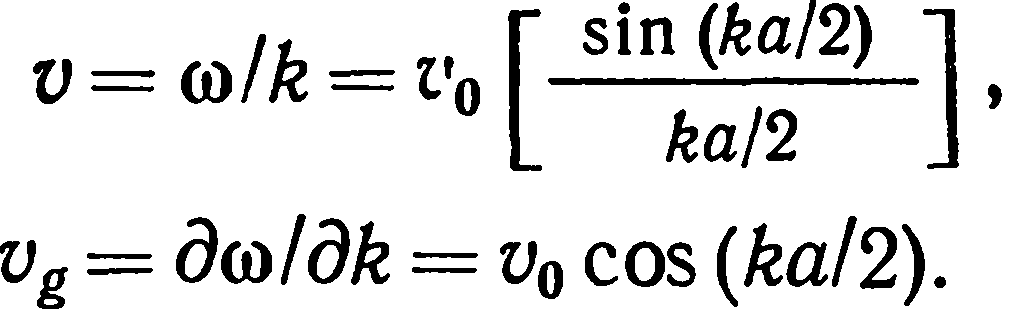. (11)

Верхняя формула для фазовой скорости волны (v), нижняя для групповой Vg.

Групповая скорость обращается в нуль, когда соседние

атомы движутся в противофазе, что происходит при 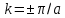или при длине волны λ=2а.

Не имеет смысла описывать прохождение волны, обеспечивающей сдвиги фаз между колебаниями соседних атомов, превышающие 180°. Поэтому не имеют физического смысла значения к, для которых 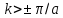(участки кривой на рис. 2, изображенные штриховой линией).

Нетрудно убедиться в том, что смещения атомов, удовлетворяющие выражению (2) для волновых векторов к, абсолютные значения которых больше 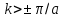, полностью эквивалентны смещениям с любым другим волновым вектором к', который удовлетворяет равенству 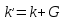, где G — вектор обратной решетки. Таким образом, первая зона Бриллюэна содержит полный спектр. Из этих замечаний очевидно, что:

волна, соответствующая границе зоны Бриллюэна, т. е. условию 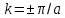, является стоячей волной, а не бегущей. Ее длина волны удовлетворяет условию брэгговского отражения на угол 180°.

В дальнейшем мы увидим, что в случае двумерного или трехмерною кристалла возбуждения (такие, как фононы или электроны) также испытывают брэгговское отражение, если их волновой вектор упирается в границу зоны Бриллюэна. В случае более чем одного измерения волна с волновым вектором к, соответствующим границе зоны Бриллюэна, в реальном пространстве должна иметь нулевую компоненту групповой скорости в направлении, перпендикулярном границе зоны Бриллюэна (представляющей собой линию или поверхность в пространстве волновых векторов к).

Волна, у которой угловая частота больше, чем 𝜔_m=(2μ/m)²=2(v₀/a), не может распространяться в воображаемом одномерном кристалле, поскольку в соответствии с выражением (6) она должна иметь комплексное значение волнового вектора. Наличие мнимой компоненты волнового вектора приводит к сильному затуханию волны.

Таким образом, волны, для которых 𝜔>𝜔_m, лежат в запрещенной области частотного спектра. Мы убедимся, что этот вывод вполне справедлив и для реальных трехмерных кристаллов.

ТРЕХМЕРНЫЙ СЛУЧАЙ

Дисперсионные кривые для трехмерного случая соответствуют уравнению (8) и рис.2 по каждой из кристаллических осей [100]- рисунки слева; [110] – рисунки в центре; [111]– рисунки справа.

Следующий рис. 3 для информации

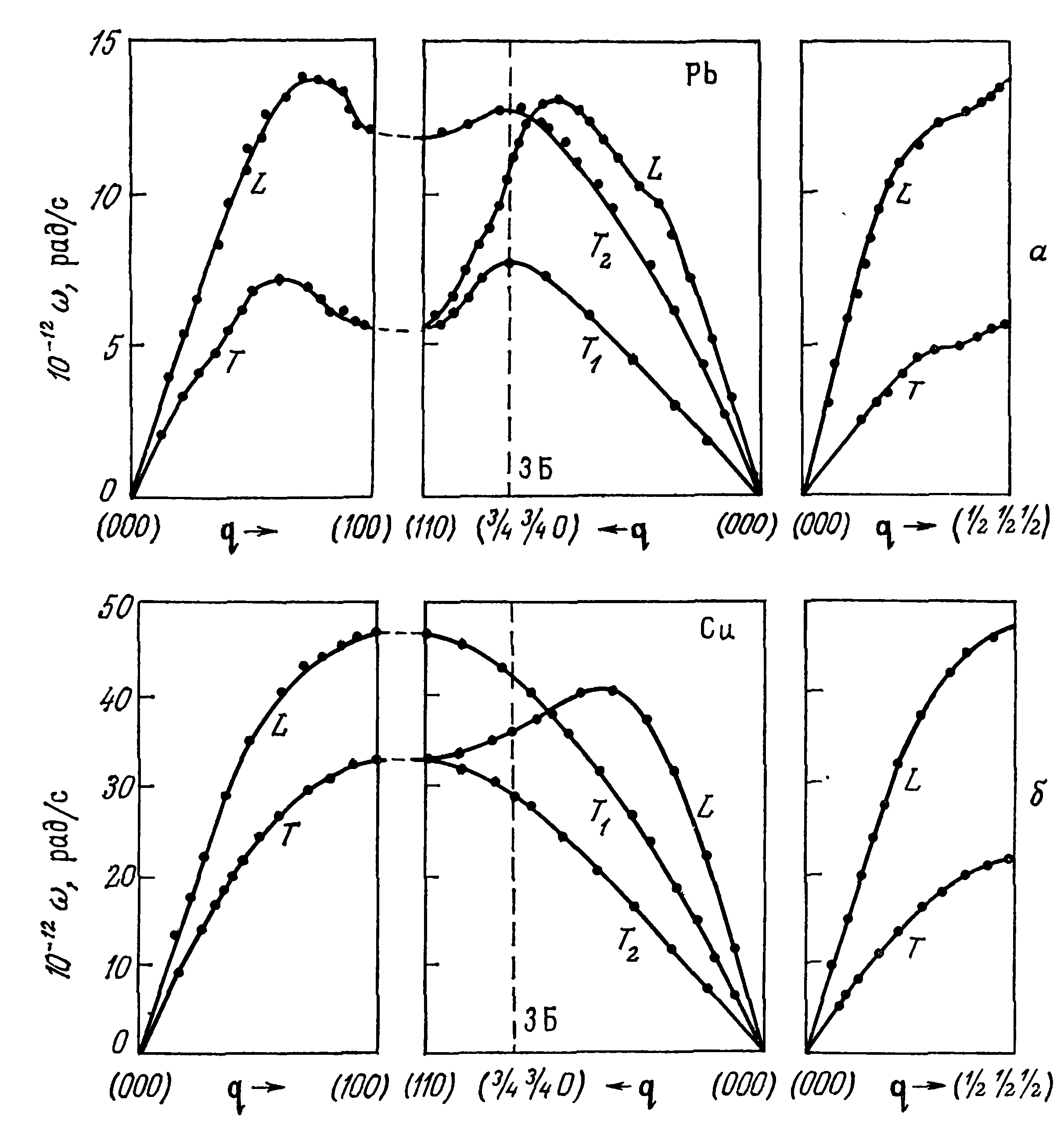
Рис. 3. Дисперсионные кривые фононов для свинца (а) и меди (б), кристаллизующихся в г. ц. к.-структуре. Угловая частота со приведена как функция безразмерного вектора q=ka/ji, измеряемого от центра зоны Бриллюэна в трех основных кристаллографических направлениях. Для направления [110] – в центре, кривые продолжены за границу зоны Бриллюэна (ЗБ). Все кривые получены с помощью неупругого рассеяния пучка монохроматических нейтронов.

Данные для свинца взяты из работы: Brockhouse et al.— Phys. Rev., 128, 1099 (1962),

для меди из работы: Svensson et al— Phys. Rev., 155, 619 (1967); Nilsson G., Roland- son S.— Phys. Rev., B7, 2393 (1973).

Для справки – расположение плоскостей [100]; [110]; [111]

Число мод; плотность состояний

В упругой среде могут возбуждаться любые колебания, однако число различающихся друг от друга мод колебаний решетки конечного размера из дискретных атомов строго ограниченно.

Для того чтобы найти распределение этих мод по частотам или волновым векторам, рассмотрим линейную одноатомную цепочку из N+1 атомов, имеющую длину Na.

Предположим, что концевые атомы, находящиеся на концах цепочки, закреплены, т. е. u₁=0 b u_N+1=0 (аналог - струна, закрепленная на концах). Тогда в этой цепочке могут возбудиться лишь такие продольные и поперечные колебания, для которых на длине Na уложится 1, 2, 3... или N полуволн. (Вспомните условие возникновения стоячих волн в струне, закрепленной на концах). Волновые векторы этих разрешенных колебательных мод удовлетворяют соотношениям

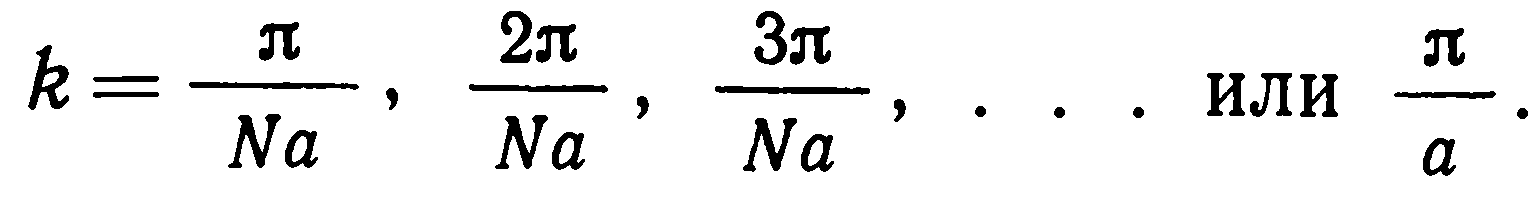(12)

Эти колебания разделены одинаковыми интервалами.

Разумеется, при больших N интервал очень мал, и при этом удобно ввести число состояний (число различимых

колебательных мод).

В области от k до k+dk число состояний равно (Na/π)dk.

Введем плотность состояний g(k), т.е. число состояний в единице объема k - пространства. Для одномерного кристалла g(k) ­– число состояний на

единичный интервал k в пространстве волновых чисел..

При этом число состояний одномерного кристалла в интервале dk, запишется через плотность состояний g(k),

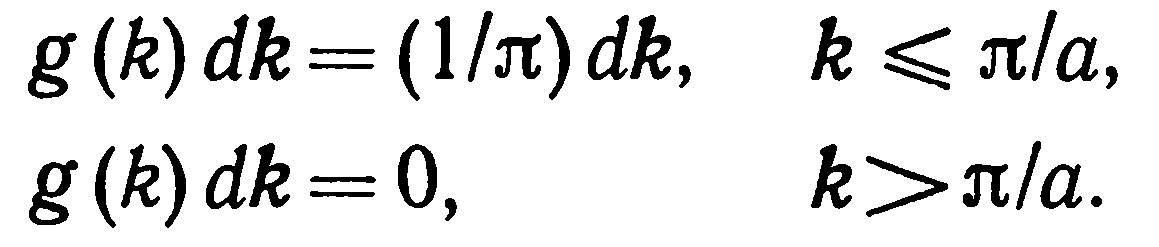(13)

Для выбранного нами одномерного случая мы получили, что g(k) не зависит от k в разрешенном спектральном интервале. В дальнейшем мы увидим, что для значительной части других случаев g(k) имеет явную зависимость от k.

Периодические граничные условия Борна-Кармана

Может показаться, что приведенный выше расчет плотности состояний не совсем правильный из-за принятых нами допущений о закреплении атомов на концах линейной конечной цепочки (поскольку такое условие приводит к тому, что существуют только стоячие, а не бегущие волны).

Рассмотрим бесконечную линейную цепочку атомов, расположенных на расстояниях а друг от друга. Пусть в ней распространяются бегущие волны.

Введем ограничение, называемое Периодические граничные условия Борна-Кармана: смещения в любой разрешенной моде повторяются через расстояние L = Na. Таким образом, мы имеем u_r=u _N+r и т. д.

Моды, которые могут распространяться при этих условиях, должны иметь следующие волновые векторы:

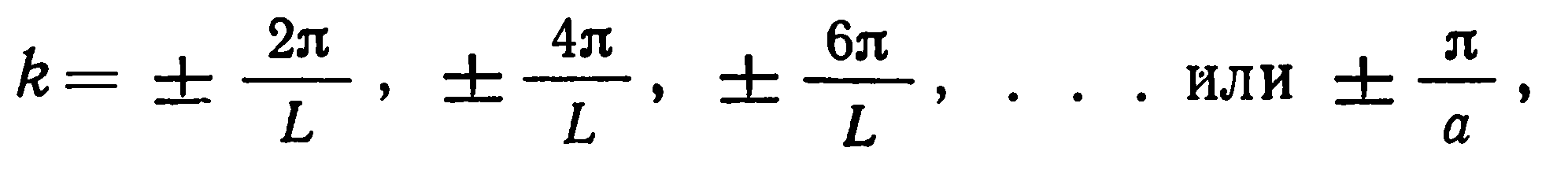, (14)

где знаки плюс и минус соответствуют волнам, распространяющимся в противоположные стороны.

Из сравнения выражений (12) и (14) следует, что в случае одномерного кристалла для стоячих или бегущих волн плотность состояний g(k) на единичный интервал |к| равна 1/π (1/2π для отрицательных K+ 1/2π для отрицательных K).

ВЫВОД: плотность состояний бесконечной цепочки не зависит от наложенных граничных условий. Вывод может быть распространен на трехмерный кристалл большого размера.

Но бесконечная линейная цепочка атомов — это не то, с чем мы имеем дело в реальности.

Однако полученный нами факт, что граничные условия не играют существенной роли для линейной цепочки, позволяет утверждать, что в реальном трехмерном кристалле плотность состояний как функция волнового вектора, частоты или энергии не зависит от формы и природы поверхности кристалла, но лишь при условии, что размеры кристалла значительно превышают атомные размеры.

В задачах физики твердого тела нередко встречаются

случаи, когда необходимо знать зависимость плотности состояний не только от k – g(k), но и от 𝜔 – g(𝜔).

Для линейной одноатомной цепочки, которую мы только что рассмотрели, можно записать

(15)

А поскольку, согласно (8)

(16)

мы имеем для групповой скорости

. (17)

Подставляя это выражение в (15), получаем для плотности состояний фотонов

(18)

Таким образом, g(𝜔) имеет явную зависимость от 𝜔 и

действительно обращается в бесконечность на верхнем пределе.

К этому выражению для g(𝜔) мы будем нередко обращаться, а при рассмотрении квантовой теории теплоемкости в разд. 2.4 мы будем иметь дело с более сложным выражением для g(𝜔).

Мы видели, что разрешенные моды для линейной цепочки с заданной периодичностью на длине L образуют последовательность точек в одномерном k-пространстве, расстояние между которыми равно 2π/L. Это представление иллюстрируется рис. 4а.

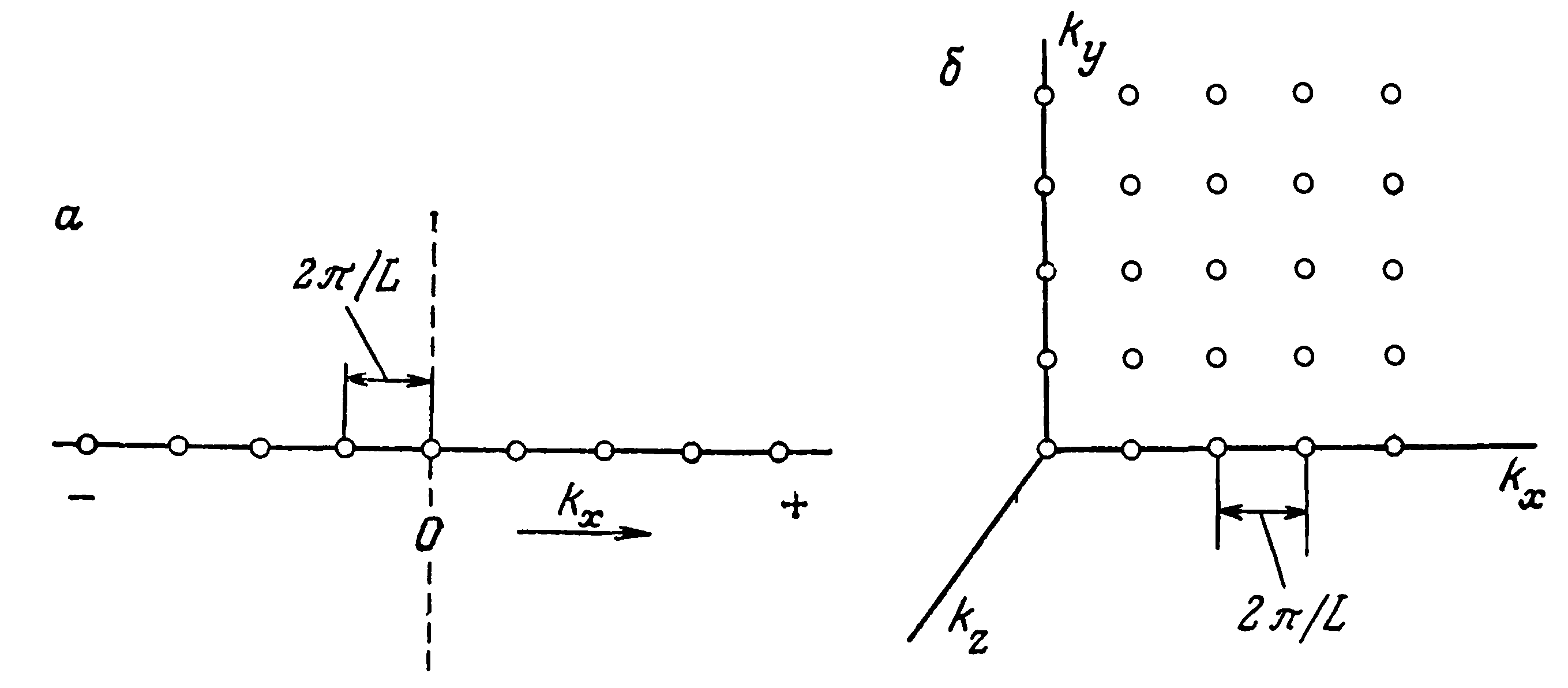
Рис. 4. Распределение разрешенных колебательных состояний в к-пространстве, когда периодичность задается длиной L. а — для одноатомной линейной решетки; б — для трехмерной решетки; показаны состояния лишь в положительном квадранте плоскости kxky.

Такое же представление можно применить к разрешенным модам в k-пространстве для трехмерного кристалла. На рис. 4б в целях удобства изображено всего лишь несколько разрешенных мод, все остальные смещения разрешенных мод должны быть периодическими с периодом L вдоль каждой оси декартовых координат. Из рисунка видно, что в k-пространстве каждое разрешенное состояние занимает объем (2π/L )³.

Поскольку объем шарового слоя радиусом K=|k| и толщиной dk с центром в начале координат равен 4πk²dk, число разрешенных колебательных состояний в интервале dk должно быть равно

(19)

Изображенное на рис. 4б распределение мод в k-пространстве будет простираться до границ зоны Бриллюэна во всех направлениях.

В случае трехмерного кристалла вывод зависимости g(𝜔) оказывается значительно более сложным, чем для

одномерного кристалла, хотя совсем нетрудно показать, что

в низкочастотной бездисперсионной области g(𝜔) может изменяться как 𝜔² (см. задачу 2.4).

Вычисление полного числа мод является сложной задачей для большинства реальных кристаллов, но, к счастью, мы можем воспользоваться тем, что

любая совокупность N атомов в трехмерном пространстве в целом может колебаться 3N различными способами. Разумеется, это число 3N равно числу классических степеней свободы у N атомов.

Две трети из этих 3N мод (т. е. 2N) соответствуют поперечным волнам и одна треть (N) — продольным. На языке к-пространства это означает, что в объеме зоны Бриллюэна, соответствующей кристаллической структуре, могут разместиться все продольные моды по одной на каждый атом и, кроме того, все поперечные моды из расчета по две моды на каждый атом.

Если мы отрежем часть кристалла, то объем зоны Бриллюэна не изменится, но точки в k-пространстве, соответствующие различным колебательным состояниям, раздвигаются.

Чтобы обосновать высказанное выше утверждение о том, что в трехмерном пространстве для N одинаковых атомов существует N продольных и 2N поперечных мод, рассмотрим простой кубический кристалл с боковыми ребрами длиной L,

так что N=(L/a)³. В этом случае зона Бриллюэна представляет собой куб с длиной ребра 2π/а и объемом (2π/а)³. Поскольку, как это видно из рис. 4б, каждая разрешенная продольная мода занимает объем (2π/а)³, во всей зоне помещается, как и ожидалось, N состояний.

Дисперсионные кривые для продольных и поперечных фононов в кристаллографических направлениях высокой симметрии могут дать информацию о наиболее важных атомных силовых постоянных.

Примеры этих кривых приведены на рис. 5.

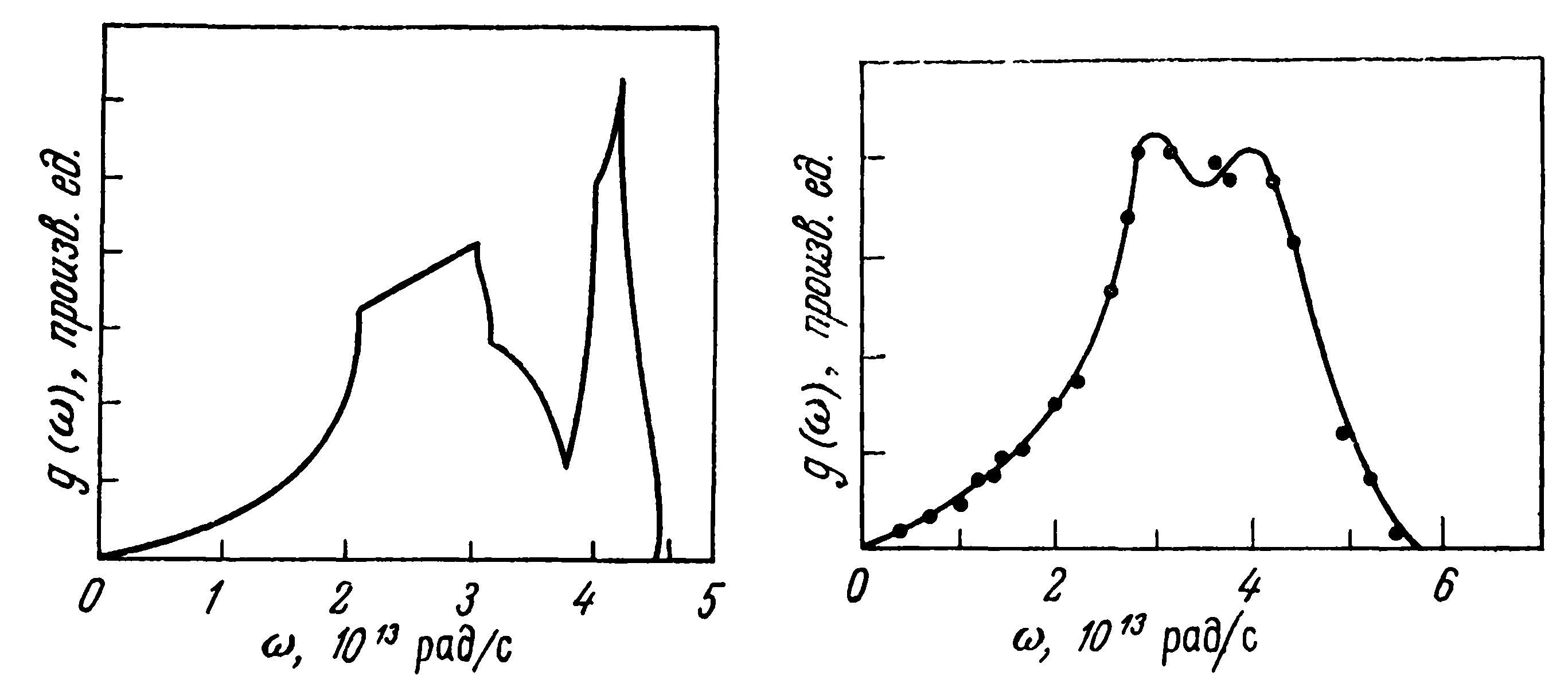
Рис. 5.-Левый Общая плотность колебательных состояний в меди как функция частоты 𝜔. Кривая построена по результатам численного анализа разных ветвей экспериментальных дисперсионных кривых на рис. 4б. [Svensson Е. С. et al— Phys. Rev., 155, 619 (1967).]

Рис. 5-Правый. Общая плотность колебательных состояний в ванадии как функция частоты 𝜔. Кривая, построенная по результатам исследования некогерентного рассеяния нейтронов, заимствована из работы:

Stewart А. Т., Brockhouse В. N.— Rev. Mod. Phys., 30, 250 (1958). Эта

кривая существенно отличается от результатов работы Картера и др.

[Carter R. S. et al.— Phys. Rev., 104, 271 (1956)], в которой указывается

на трудности такого рода экспериментов.

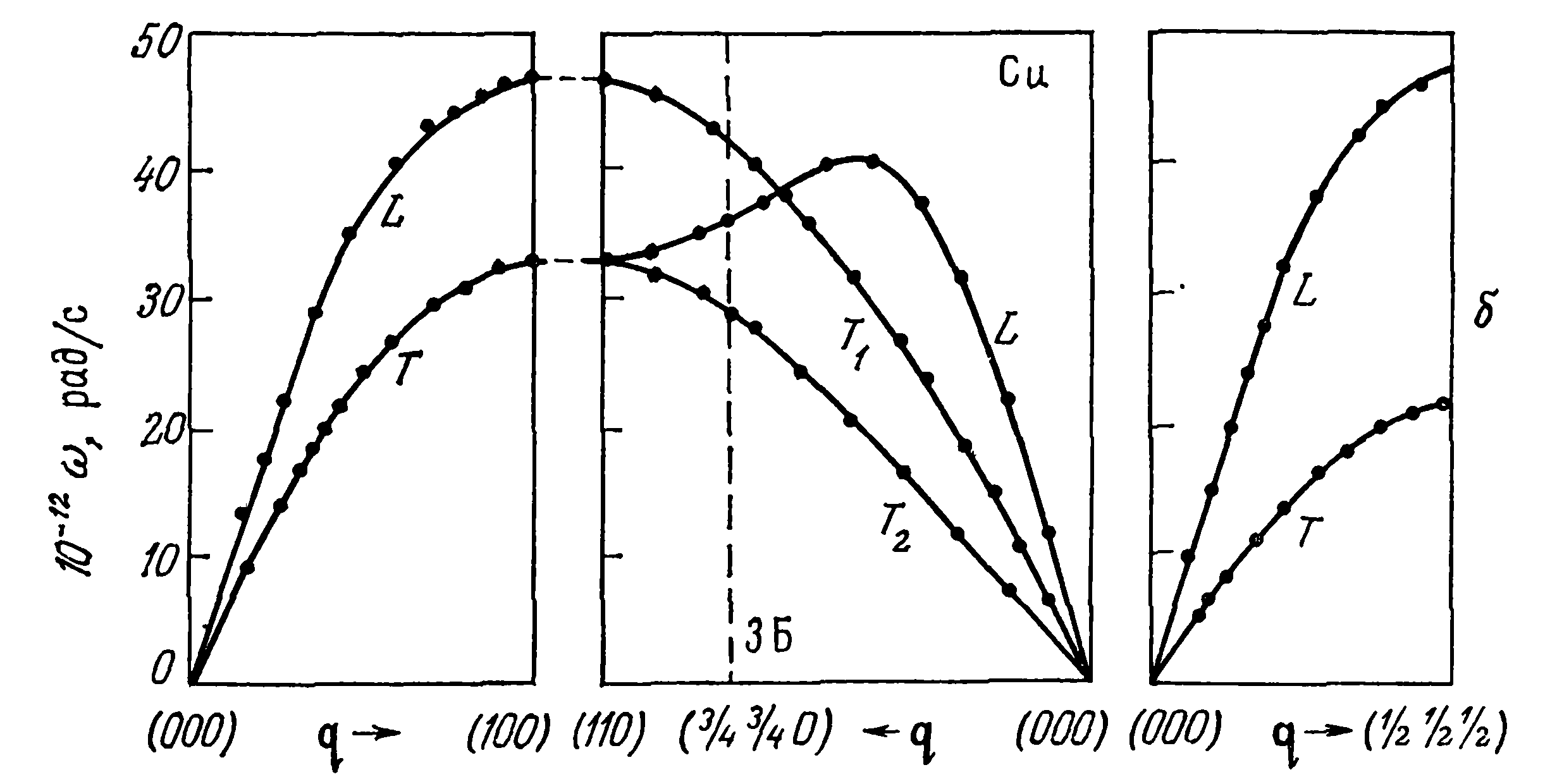
Кривые, которые для меди, которые обрабатывались, чтобы получить кривые 5-Левый

Острые пики и резкие перегибы имеются у кривых на рис. 5; особенно ярко они выражены на кривой на рис. 5-Левый. Значения 𝜔, при которых кривые g(𝜔) имеют резкие перегибы, называются критическими точками, или особенностями Ван Хова. Этим значениям угловых частот соответствуют нулевые групповые скорости фононов в некоторых направлениях, поскольку на границе зоны Бриллюэна изменяется топология поверхности постоянной 𝜔 в к-пространстве.

Например, самый большой пик на кривой на рис. 5 –Левый соответствует максимальной разрешенной частоте продольных фононов для направления [110]; аналогичным образом наклон кривой g(𝜔) резко уменьшается при частоте, при которой кривая дисперсии поперечных фононов совпадает с границей зоны Бриллюэна для направления [111].

Колебательный спектр решетки с базисом

До сих пор мы ограничивались обсуждением структур, в которых базис состоит из одного атома. В спектре более сложных структур, в которых на элементарный базис приходится два или больше атомов (независимо от того, являются ли они атомами одного или разных химических элементов), появляются дополнительные особенности. Наиболее примечательной особенностью является чередование разрешенных и запрещенных частотных интервалов.

Чтобы понять, надо выяснить: каким образом возникает чередование областей с вещественными и комплексными к, на примере колебаний решетки. В дальнейшем это поможет нам понять аналогичное явление в электронном спектре кристаллов.

Пусть кристалл состоит из атомов двух сортов.

Нормальные колебания линейной двухатомной цепочки рис. 6.

Эта цепочка отличается от кристалла, изображенного на

рис. 1, только тем, что в нем чередуются атомы с массами М и m. Предположим, что m<М. Если теперь в кристалле возбуждается продольное возмущение, распространяющееся вдоль цепочки, колебания двух сортов атомов обычно имеют различные амплитуды

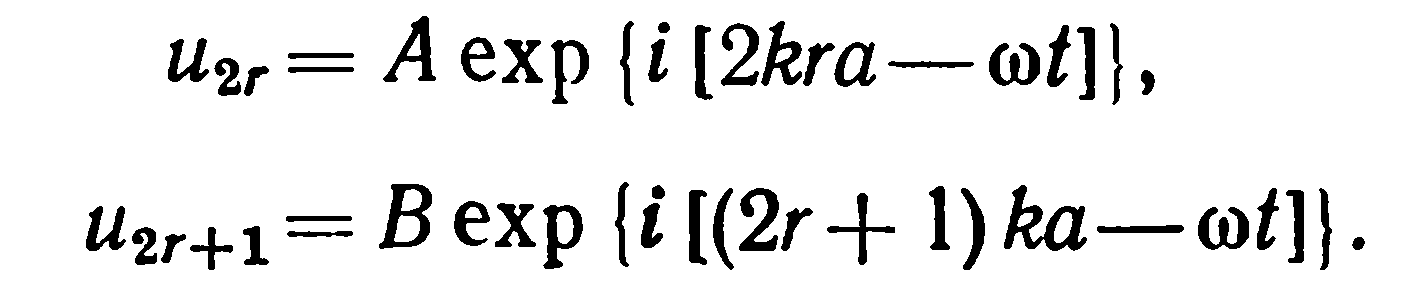(20)

Предположим, что возвращающая сила обусловлена только ближайшими соседями и что смещения не выходят за пределы упругой области, в которой применим закон Гука.

Тогда уравнения Ньютона для смещений u_2r и u_2r+1 можно записать в таком же виде, как и уравнения (5) и (6) для линейной одноатомной цепочки

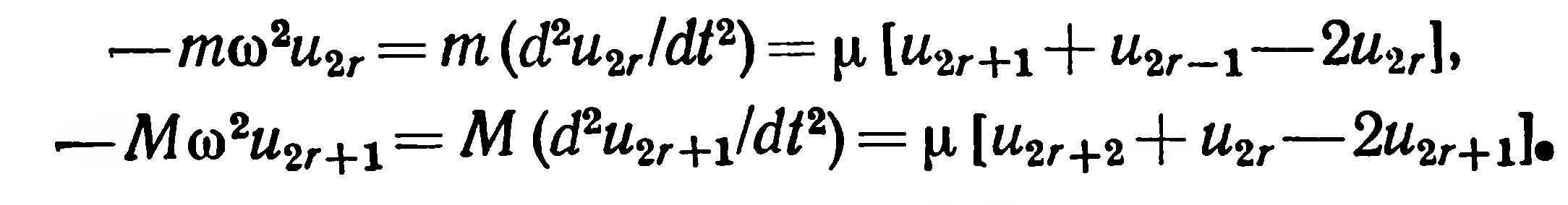(21)

Рис. 6. Последовательность соседних атомов в линейной двухатомной цепочке. Масса т атомов меньших размеров меньше массы М больших атомов. Следует заметить, что размер элементарной ячейки, которым определяется размер зоны Вриллюэна, в этом случае равен 2а.

Подставляя (20) в (21), получаем два совместных

уравнения:

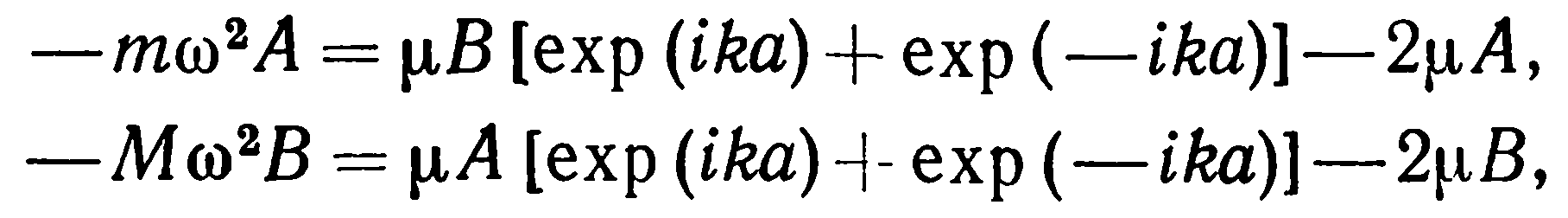(22)

которые можно представить в следующем виде:

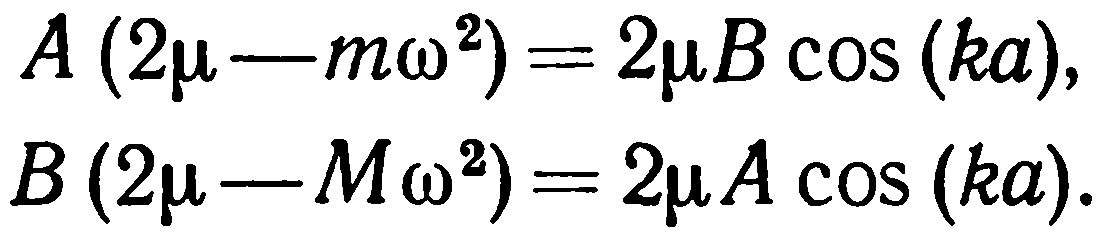(23)

Исключив A и В из этих уравнений, получим зависимость

между k и 𝜔, т. е. дисперсионное соотношение:

(24)

откуда находим дисперсионное соотношение в виде

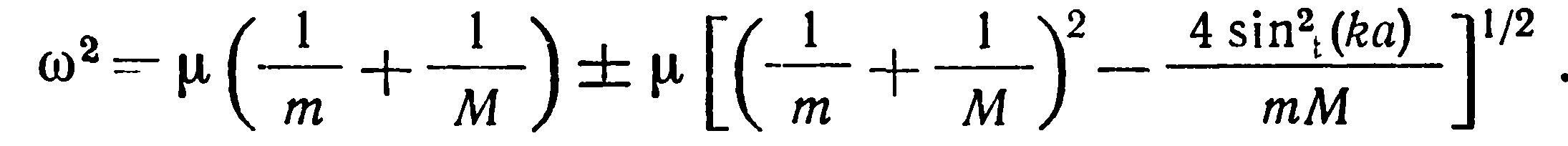(25)

Для линейной одноатомной цепочки, как было показано, существуют одно решение для k>0 (волна, бегущая вправо) и одно для k<0 (волна, бегущая влево).

Спектр 𝜔(k) является однозначным.

В рассматриваемом случае двухатомной цепочки

спектр 𝜔(k) является двузначным, частота является двузначной функцией волнового вектора k (см. рис. 7)

Данному к даже в положительном квадранте соответствуют два решения для 𝜔.

Нижняя ветвь спектра на рис. 7 описывается формулой (25) с отрицательным знаком. Эта ветвь обычно называется акустической ветвью, она соответствует спектру, который уже был получен нами для одноатомной цепочки,

за исключением двух следующих особенностей.

1. Для любой совокупности смещений в цепочке, состоящей из атомов двух видов, абсолютная величина волнового вектора не превышает (π/2а), в то время как для одноатомной линейной цепочки граница зон Бриллюэна лежит в точках ± (π/а). Это связано с тем, что в двухатомной цепочке размеры зоны Бриллюэна определяются периодом 2а, а не расстоянием между ближайшими соседями.

2. Из формулы (25) следует, что максимальная возможная угловая частота акустических колебаний не зависит от массы более легких атомов в цепочке и равна

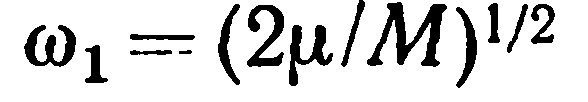(26)

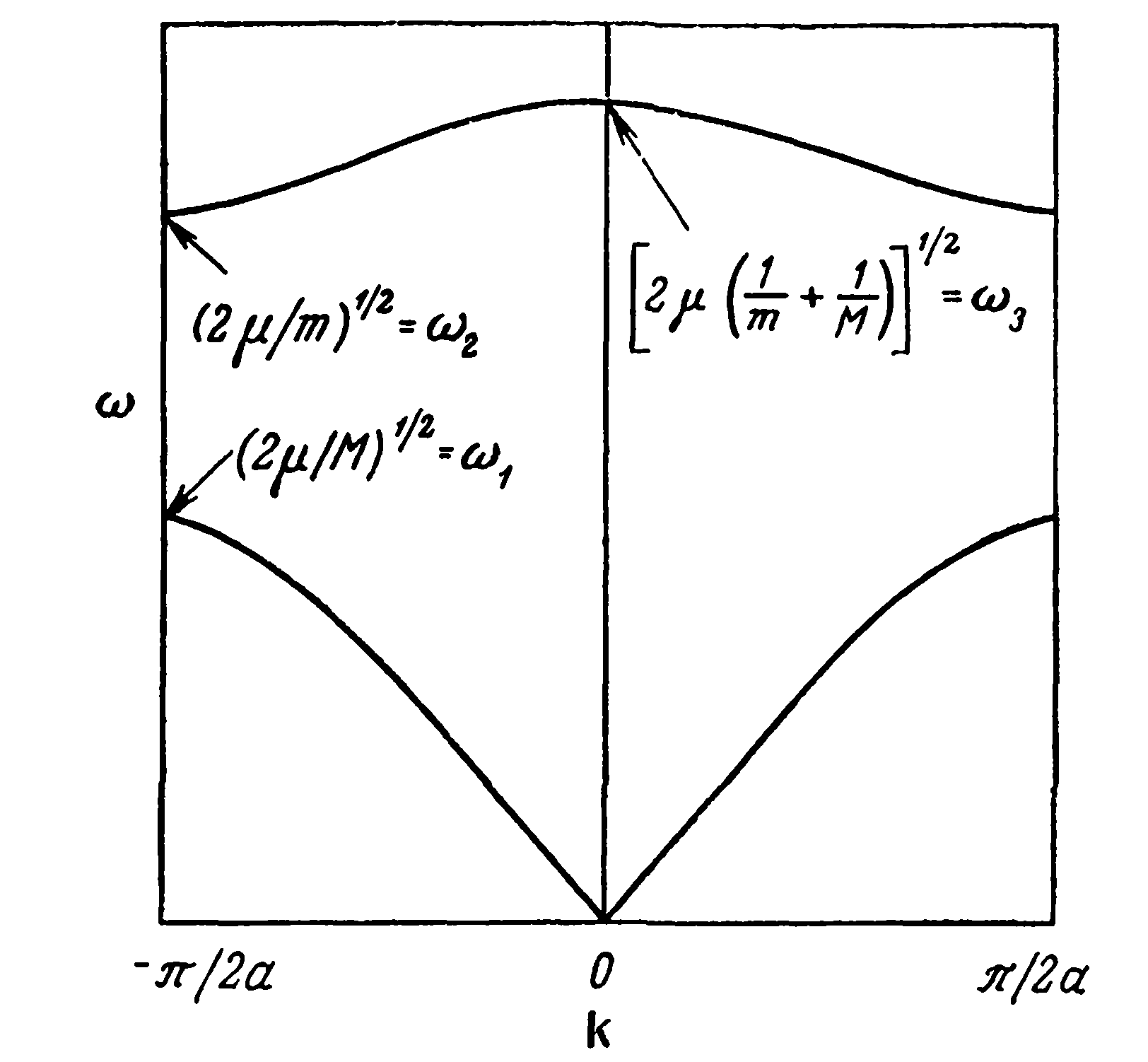
Рис. 7. Дисперсионные кривые для продольной волны, распространяющейся в линейной двухатомной решетке. Первая зона Бриллюэна охватывает область k-пространства, для которой |к|^я/2а. Нижняя кривая (которую можно сравнить с кривой на рис. 2.3) является акустической ветвью, а верхняя — оптической ветвью колебательного спектра.

Особенность (26) можно понять, если рассмотреть зависимость отношения амплитуд колебаний двух сортов атомов от частоты. Из уравнений (23) получаем

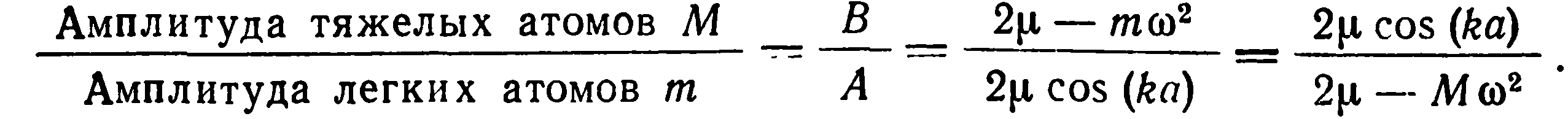(27)

Таким образом, отношение амплитуд почти равно единице (все атомы движутся одинаково) в случае длинных волн и низких частот, т. е. для акустических волн, для которых выполняются следующие условия:

(28)

При увеличении к и 𝜔 в акустической ветви возрастает

крайняя правая часть равенства (27), при этом возрастает также и отношение В/А. В предельном случае, когда

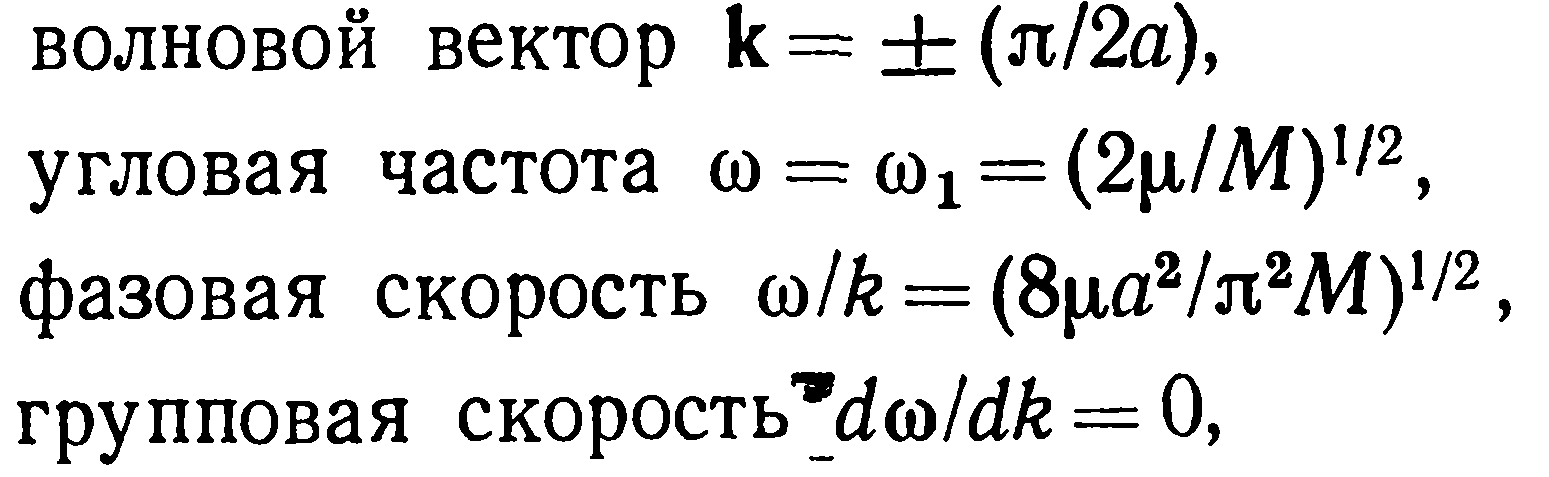(29)

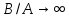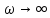получаем, что при . Это означает, что

амплитуда A должна быть равна нулю независимо от величины В. Поскольку более легкие атомы не движутся в предельном режиме колебаний на частоте 𝜔₁ не удивительно, что величина m не входит в выражение (26) для 𝜔₁.

Запрещенная зона для колебаний.

В некотором интервале частот, превышающих угловую частоту 𝜔₁ не существует решений для вещественных к. Аналогичную ситуацию мы имеем в случае одноатомной цепочки для всех частот выше 𝜔_m. Область частот, соответствующих комплексным значениям к, образует

запрещенную зону, поскольку любая волна, возбуждаемая на частоте, лежащей в этом диапазоне, будет сильно затухать.