Л6 Кр РЕШЕТКА

Л6. Кристаллическая решетка

Всякое обсуждение свойств твердого тела должно начинаться с определения геометрической структуры, которой приблизительно соответствует расположение атомов. Этой геометрической структурой является кристаллическая решетка —упорядоченный набор положений, или точек в трехмерном пространстве, занимаемых атомами, когда вся система в целом находится в основном состоянии.

Такое описание представляет собой некоторую идеализацию. В реальных* кристаллах неизбежно существуют нарушения правильности структуры: вакансии, дислокации, существуют границы зерен и т. д., так что даже в наиболее тщательно изготовленных монокристаллах, макроскопически совершенных, нельзя ожидать строгой периодичности структуры. Данное выше упрощенное определение не учитывает также существенную «размазанность» атома или иона, связанную с тем, что его электронное облако проницаемо и деформируемо, а сам атом благодаря нулевым колебаниям всегда колеблется около своего положения равновесия. Более точно можно сказать, что идеальная решетка описывает структуру твердого тела в том смысле, что локальные условия для любых двух точек кристалла, отстоящих друг от друга на таком же расстоянии, что и два узла решетки, «почти никогда» не отличаются друг от друга. Различие между «почти никогда» и «никогда» определяется возможностью попасть на примесь, вакансию, на границу зерна или, наконец, на поверхность кристалла.

Говоря математическим языком, решетка задает группу трансляций данной структуры.

Некоторые твердые тела, например стекло или каучук, не обладают никакими кристаллическими свойствами, что зачастую приводит к необходимости изучать их, применяя более трудные методы, развитые в теории жидкостей.

Конкретное аналитическое представление решетки несколько условно.

Решетку разбивают на равные геометрически тождественные многогранники, которые называют элементарными ячейками. Элементарные ячейки могут быть совмещены друг с другом путем сдвига на векторы вида

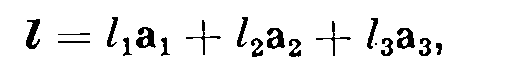(1)

где а1, а2, а3 — три фиксированных вектора (базисные или главные векторы решетки), a l1, l2, l3 —три целых числа, значения которых лежат в пределах, ограниченных размерами и формой самого кристалла. Чтобы представить себе решетку, построим в трехмерном пространстве все точки, определяемые равенством (1), и каждую такую точку окружим элементарной ячейкой, содержащей реальные атомы.

Этот способ, очевидно, не единственный. Беря группу ячеек, определенных по одному рецепту, мы можем построить элементарные ячейки, соответствующие другому рецепту, с другими базисными векторами. Очевидно, желательно выбрать простейшую элементарную ячейку, содержащую минимальное число атомов.

Решетка, в которой элементарная ячейка содержит только один атом (или сильно связанную молекулу), называется решеткой Браво. В противном случае мы говорим о решетке с базисом.

Слово базис означает совокупность векторов b2, b3, ...,bt, определяющих

положение частиц (r) в ячейке относительно какой-нибудь из этих частиц, принятой за начало отсчета.

Критерием, позволяющим определять, является ли данная решетка решеткой Бравэ, служит следующее свойство решетки БРАВЕ. Если (+г) —вектор, соединяющий данную точку О с любой другой точкой решетки, то вектор (— г ) тоже соединяет О с точкой решетки.

Для некоторых целей решетки Бравэ иногда разбивают на элементарные ячейки, содержащие более одного атома. В интересующих нас задачах, однако, это было бы весьма неудобно.

Даже после того, как задана группа трансляций, остается еще не-

которая свобода в определении элементарной ячейки. Например, остается неопределенным (в решетке Бравэ), где находится атом —в центре или в углу ячейки? В этом случае мы примем определение элементарной ячейки, данное Вигнером и Зейтцем.

Ячейка Вигнера-Зейтца представляет собой область, ограниченную совокупностью плоскостей, равноотстоящих от атома и от его ближайщих соседей. Она обладает тем свойством, что все точки решетки, принадлежащие ячейке, находятся ближе к центру ячейки, чем любые другие точки решетки.

Такая ячейка лучше всего аппроксимирует сферу, которую мы интуитивно связываем с каждым атомом, прежде чем «упаковать» его в кристалл.

Надо знать также истинные физические размеры решетки. Пусть объем всего кристалла равен V и в единице объема содержится N элементарных ячеек. Пусть, далее, каждая ячейка имеет объем v_с. В кубической решетке объем элементарной ячейки равен а3, где а—длина базисного вектора. Будем использовать букву а для обозначения постоянной решетки, определяемой как кубический корень из объема элементарной ячейки, даже если сама ячейка не кубическая.

В решетке Бравэ объем элементарной ячейки равен атомному объему v, и в дальнейшем мы обычно не будем делать различий между ними.

Полезно ввести другую величину г, которую назовем атомным радиусом и определим как радиус сферы с объемом равным объему элементарной ячейки v (иногда называемой сферой Вигнера-Зейтца из-за ее сходства с ячейкой Вигнера-Зейтца).

В кристаллах химических соединений эти параметры дают слишком усредненную характеристику решетки и потому не очень полезны;

однако в простых кристаллах они оказываются очень удобными для работы в атомной шкале, когда длины оцениваются по сравнению с размерами атомов. При оценках следует иметь в виду, что большинство элементов имеет атомный радиус порядка 2 А.

Примитивная ячейка, являющаяся ячейкой с минимальным объемом, представляет собой частный случай элементарной ячейки.

Примитивная ячейка прямой решетки Браве, называется ячейкой Вигнера-Зейтца

Объем примитивной ячейки обратной решетки равен обратной величине объема примитивной ячейки прямой решетки

Ячейка Вигнера — Зейтца́ — область пространства, с центром в некоторой точке решётки Браве, которая лежит ближе к этой точке решётки, чем к какой-либо другой точке решётки.

Ячейка Вингера — Зейтца это примитивная ячейка, обладающая полной симметрией решётки Браве.

На ячейку Вигнера — Зейтца (как и на любую другую элементарную ячейку) приходится один узел решётки Браве.

Элементарная ячейка обратной решётки в форме ячейки Вигнера-Зейтца в обратном пространстве есть первая зона Бриллюэна

Построение

Выбирается произвольный узел решётки Браве и соединяется со всеми ближайшими соседними узлами. Через середины этих отрезков проводим перпендикулярные отрезкам плоскости. Ограниченная плоскостями область наименьшего объёма будет являться ячейкой Вигнера — Зейтца.

Элементарная ячейка в форме ячейки

Вигнера — Зейтца для 2-мерной решётки

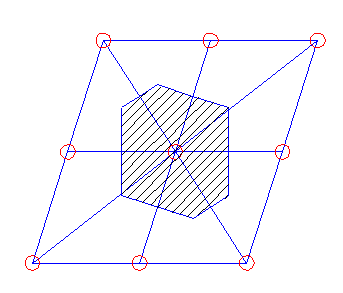
Ячейка Вигнера — Зейтца для объёмноцентрированной кубической решётки кристалла

БРИЛЛЮЭ́НА ЗО́НЫ, области значений волнового вектора k, при которых энергия электронов изменяется непрерывно, а на границах претерпевает разрыв. Понятие зон Бриллюэна используется в теории твердого тела. Предложено Л. Бриллюэном в 1930 г.

Волновой вектор k является одной из основных характеристик состояния электрона в твердом теле. В соответствии с зонной теорией, электрон в кристалле не может иметь непрерывный спектр значений энергий, поэтому и на зависимости энергии электронов Е(k) также должны быть исключены участки, соответствующие запрещенным зонам, т. е. кривая Е(k) должна иметь разрывы в некоторых точках.

Состояния электрона в зоне, характеризуемые волновым вектором k, изображают в k-пространстве, где на трех взаимно перпендикулярных осях координат откладывают составляющие вектора kx, ky, kz. Если в k-пространстве от начала координат отложить векторы k, соответствующие возможным состояниям движения электрона, то концы таких векторов для всех состояний зоны при этом оказываются лежащими в некотором многограннике, который и называется зоной Бриллюэна. Иногда для наглядности k-пространство разделяют на малые ячейки, количество которых равно числу возможных векторов k. Тогда каждая ячейка будет соответствовать в данной зоне двум состояниям электрона с противоположно направленными спинами.

Так как k -пространство отличается от пространства обратной решетки только масштабом, переход от элементарной ячейки обратной решетки к элементарной ячейке фазового пространства производят с помощью множителя 2 по каждой из осей обратной решетки.

Таким образом, построение первой зоны Бриллюэна можно осуществить следующим образом. Сначала строится обратная решетка, затем с помощью множителя 2 осуществляется переход в k-пространство. После этого любой узел обратной решетки соединяют прямыми линиями с другими ближайшими соседними узлами. Через середины полученных отрезков проводятся перпендикулярные плоскости. Объем, заключенный между этими плоскостями и будет первой зоной Бриллюэна. – это решетка Вигнера-Зейта в обратном пространстве

Структура зон Бриллюэна определяется только строением кристалла и не зависит от рода частиц, образующих кристалл, или от их межатомного взаимодействия. Границы зон Бриллюэна определяют условием, эквивалентным условию Вульфа-Брэгга для интерференционных максимумов при рассеянии рентгеновских лучей в кристалле. Это позволяет построить по рентгенограммам его зону Бриллюэна.

Физический смысл границ зоны Бриллюэна заключается в том, что они показывают такие значения волновых векторов или квазиимпульсов электрона, при которых электронная волна не может распространяться в твердом теле.

Существование большого числа зон Бриллюэна не означает, что необходимо рассматривать энергию электрона в каждой из них: любое состояние электрона можно выразить посредством вектора k, в пределах зоны Бриллюэна, приведенной к первой зоне.

Зона Бриллюэна — отображение ячейки Вигнера-Зейтца в обратном пространстве. В приближении волн Блоха волновая функция для периодического потенциала решётки твёрдого тела полностью описывается её поведением в первой зоне Бриллюэна.

Первая зона Бриллюэна (часто называемая просто зоной Бриллюэна) может быть построена как объём, ограниченный плоскостями, которые отстоят на равные расстояния от рассматриваемого узла обратной решётки до соседних узлов. Альтернативное определение следующее: зона Бриллюэна — множество точек в обратном пространстве, которых можно достигнуть из данного узла, не пересекая ни одной брэгговской плоскости.

Аналогичным образом можно получить вторую, третью и последующие зоны Бриллюэна. n-я зона Бриллюэна — это множество точек, которые можно достигнуть из данного узла, пересекая n-1 брэгговскую плоскость.

ФИЗИЧЕСКИЙ СМЫСЛ ЗОН БРИЛЛЮЭНА рассмотрим на примере двумерного кристалла. Построим зоны Бр. из физических принципов.

ОСНОВА: соотношение Вульфа-Брэггов для дифракции рентгеновских волн и электронов:

2asinφ=jλ, j =1,2,3.. – условие отражения здесь наблюдается разрыв в энергиях. Крайний случай φ=π/2

2a=jλ; λ=2π/k отсюда условие отражения для k, т.е. в k-пространстве

k=j π/a

В случае одномерной решетки, состоящей из одинаковых атомов, разрывы энергетического спектра имеют место при значениях волновых векторов 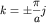, (). При этом ось значений k делится точками разрыва на отдельные участки, которые являются зонами Бриллюэна (рис.1).

Построим зоны Бриллюэна для плоской двумерной квадратной решетки с периодом a. Границы зон определяются условиями Вульфа-Брэгга, определяющими значения длин волн (волновых векторов), при которых электронные волны отражаются решеткой:

или ,

Где ,

-расстояние между параллельными отражающими плоскостями (в двумерном случае - линиями) в реальном r-пространстве, а - расстояние между соответствующими этим плоскостям границами зон Бриллюэна в k-пространстве (пространстве волновых векторов). Таким образом, каждому семейству атомных плоскостей с периодом a_i в координатном пространстве соответствует семейство параллельных плоскостей в импульсном пространстве (р-пространстве) с периодом , на которых энергия электрона испытывает разрыв. Поэтому, чтобы найти границы зон Бриллюэна, будем рассматривать последовательно семейства эквидистантных отражающих плоскостей (рис. 16), образованных атомами кристалла, начиная с семейств с максимальным периодом. К таким семействам в нашем случае относятся два взаимно перпендикулярных семейства плоскостей (линий), перпендикулярных e_x (оси х) и перпендикулярных e_y (оси у). Расстояние между отражающими плоскостями (линиями) в обоих семействах равно периоду решетки a₁=a.

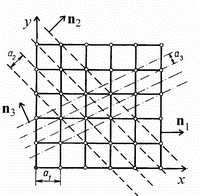
Рис. 1. Двумерная решетка в пространстве координат. Штриховыми линиями показаны линии, проходящие через узлы решетки от которых также могут отражаться электроны, расстояния между ними больше, чем между сплошными линиями

Электронные волны с волновыми векторами, имеющими компоненту k_x волнового вектора, равную 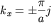(), испытывают брэгговское отражение от плоскостей первого семейства, перпендикулярных e_x. При этих значениях k_x в энергетическом спектре появляются зоны запрещенных значений энергии, то есть энергия терпит разрыв. В k-пространстве линии разрыва энергии (границы зон Бриллюэна) для таких электронов изобразятся эквидистантными линиями , перпендикулярными оси k_x (рис.2).

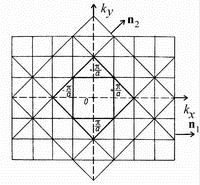
Рис. 2. Двумерная решетка в пространстве импульсов (обратная решетка-вот она зачем нам нужна). Квадрат в центре построен исходя из сплошных линий на рис.1, т.е. для наибольших расстояний между плоскостями a1=ф. Квадрат – первая зона Бриллюэна

Аналогично строятся линии разрывов энергии 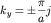, соответствующие брэгговскому отражению электронных волн от семейства плоскостей, перпендикулярных e_y.

Одно из двух семейств отражающих плоскостей (линий) в r-пространстве с периодом 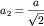и нормалью n₂ изображено на рис.1. Электронные волны, имеющие составляющую волнового вектора в направлении , перпендикулярном рассматриваемым отражающим плоскостям, испытывают брэгговское отражение. Соответствующие линии разрывов энергии в k-пространстве представляют собой эквидистантные линии, перпендикулярные n₂, (рис. 2). Аналогично строятся (рис.2) линии разрывов энергии и для второго семейства отражающих плоскостей с тем же межплоскостным расстоянием 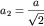, но в другом направлении.

Одно из четырех семейств плоскостей с периодом 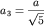и нормалью n₃ представлено на рисунке 1. Соответствующие этим семействам отрезки линий (плоскостей) разрывов энергии, перпендикулярные n₃ и отстоящие друг от друга на представлены на рисунке 3.

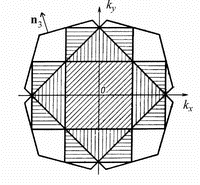
Рис. 3. Двумерные зоны Бриллюэна. Разная штриховка относится к разным зонам. Площади зон одинакова. Первая зона односвязная – квадрат в центре-косая штриховка

Линии разрывов энергии образуют границы зон Бриллюэна. Первая зона представляет собой площадь (наклонно заштрихованную на рис.3-квадрат), ограниченную совокупностью лини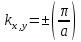й наиболее близко расположенных к началу координат. Вторая зона Бриллюэна - совокупность площадей (вертикально заштрихованных на рис.3), прилегающих к границе первой зоны и равных по площади первой зоне, третья зона - совокупность горизонтально заштрихованных площадей, четвертая - совокупность не заштрихованных площадей (рис.3). Начиная со второй, зоны становятся многосвязными.
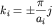