29. Оценка погрешности процесса зейделя

Пусть дана линейная система Х=+Х . Если X_i –точное значение корней линейной системы, а -k-е приближение, вычисленное по методу Зейделя, то для оценки погрешности этого метода применяется формула

_.

Пример. Подсчитать, сколько итераций по методу Зейделя необходимо выполнить, чтобы с точностью до 10^-4 найти корни системы

_.

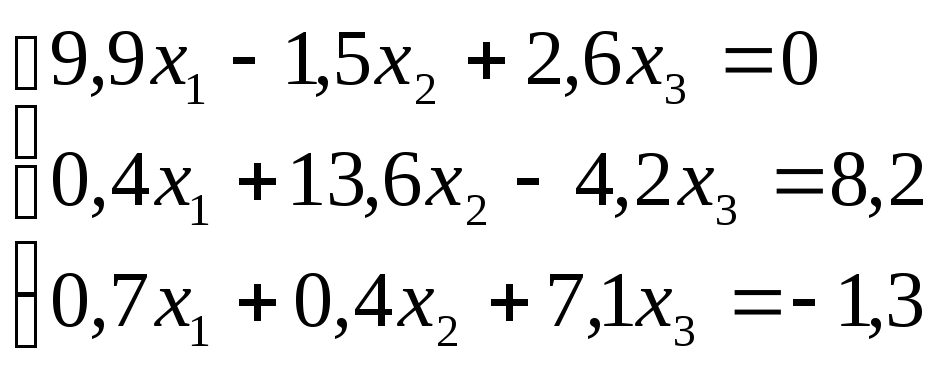Решение. 1) Приведём систему к нормальному виду (см. стр. 96)

_.

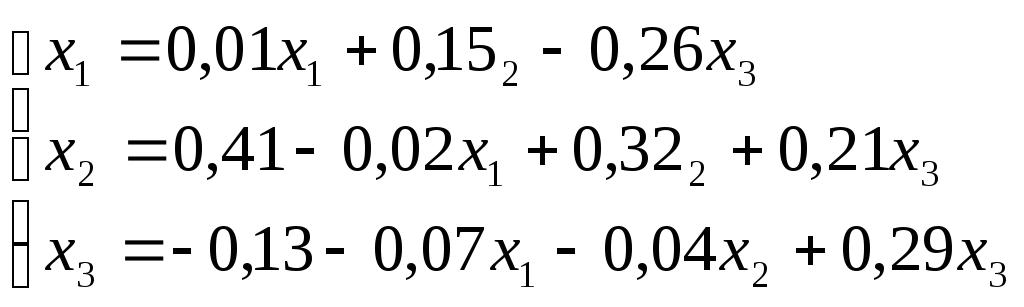2) За нулевые приближения примем столбец свободных членов =0;=0,41;= -0,13 и вычислим первые приближения

=0,01∙0+0,15∙0,41-0,26∙(-0,13)=0,0953

=0,41-0,02∙0,0953+0,32∙0,41+0,21∙(-0,13)=0,5120

= -0,13-0,07∙0,0953-0,04∙0,5120+0,29∙(-0,13)=-0,1948

3) Матрица

.

Значит, Поскольку

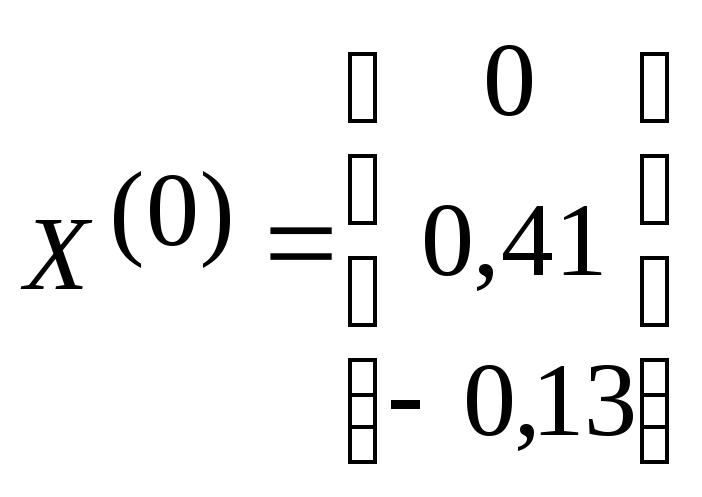и ,

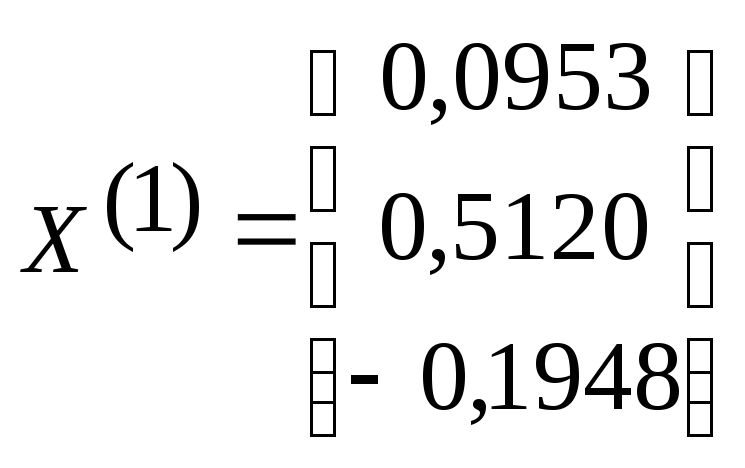имеем

т.е.

4) По формуле (1) определяем k₁:

;

Аналогично можно производить оценку метода Зейделя по норме 2.

30. Привеление системы линейных уравнений к виду, удобному для итерации

Процессы последовательных приближений и Зейделя для линейной системы Х=+Х сходятся к единственному решению независимо от выбора начального вектора, если

Таким образом, для сходимости вышеуказанных итерационных процессов достаточно, чтобы значения элементов матрицыприбыли небольшими по абсолютной величине. Это равносильно тому, что если для линейной системы AX=B модули диагональных коэффициентов каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов), то итерационные процессы для этой системы сходятся, т.е. если мы имеем систему причем то процессы последовательных приближений и Зейделя для данной системы сходится.

Применяя элементарные преобразования, линейную систему AX=B можно заменить такой эквивалентной системой Х=+Х, для которой условия сходимости будут выполнены.

Пример 1. Привести данную систему линейных уравнений к виду, удобному для итерации:

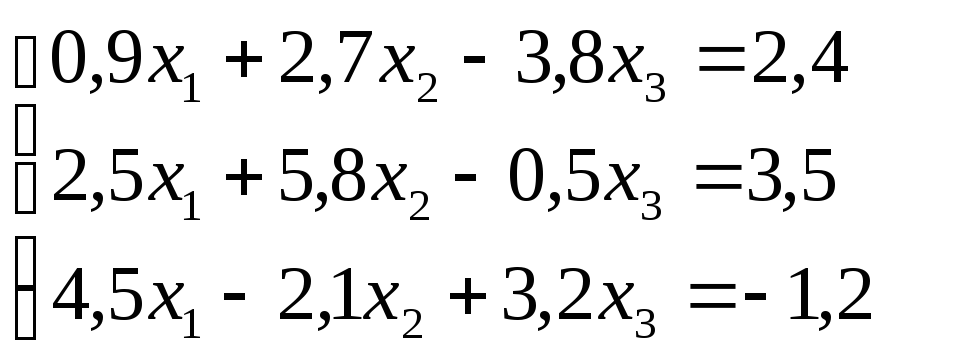
Решение. 1) Из данной системы выделяем уравнения с коэффициентами, модули которых больше суммы модулей основанных коэффициентов системы. Каждое выделенное уравнение выписываем в такую строку новой системы, чтобы наибольший по модулю коэффициент оказался диагональным.

В уравнении (Б) коэффициент при по модулю больше суммы модулей остальных коэффициентов. Принимаем уравнение (Б) за второе уравнение новой системы.

(1)

2) Из оставшихся неиспользованных уравнений системы оставляем линейно независимые между собой комбинации. Так, за первое уравнение новой системы можно взять линейную комбинацию (2В)+(А), тогда имеем

(2)

За третье уравнение новой системы можно принять линейную комбинацию (2А)-(Б), т.е.

_. (3)

3) В итоге получаем преобразованную систему линейных уравнений (1), (2), (3), эквивалентную исходной и удовлетворяющую условиям сходимости итерационного процесса:

(*)

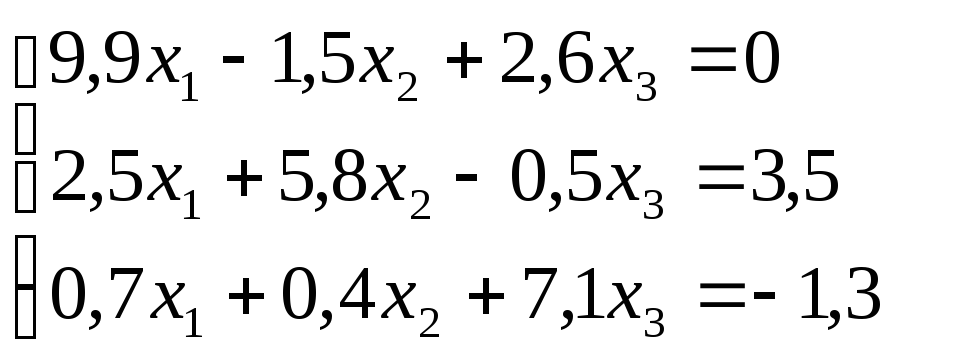Приведя систему (*) к нормальному виду, имеем

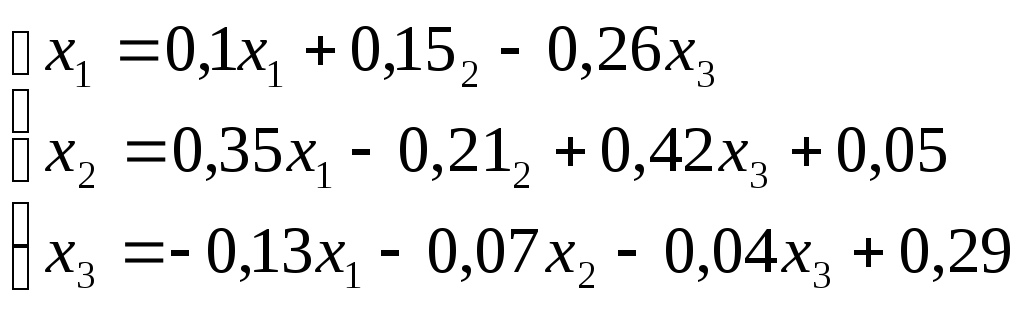
Остается решить систему одним из итерационных методов.