Введение

Линейная алгебра – один из важнейших разделов современной математики. Основные понятия этой математической дисциплины находят применение как в различных теоретических исследованиях, так и для решения многих практических задач. В последнее время линейную алгебру стали широко применять в экономике, она является теоретической базой линейного программирования – одного из разделов математического программирования, который используется для решения целого ряда экономических задач.

Цель данного пособия – научить студентов самостоятельно решать задачи по основным разделам курса «Линейная алгебра», дать необходимый минимальный объем знаний по теоретическому курсу.

В пособии рассмотрены системы линейных уравнений, элементарная теория матриц, теория определителей, векторная алгебра, задачи линейного программирования. Раскрывается экономический смысл математических понятий, приводятся простейшие приложения линейной алгебры в экономике. В начале каждого параграфа дается сжатое теоретическое введение, содержатся основные определения, формулировки важнейших теорем и главнейшие формулы. Затем приводится решение одной или нескольких характерных задач. Далее помещены задачи для самостоятельного решения. Особо обращаем внимание студентов на многочисленные примеры и упражнения, значительная часть которых обычно предлагается во время экзамена. Предусмотрено выполнение студентами самостоятельной работы, включающей задания по каждому из разделов пособия. Приведен список экзаменационных вопросов.

1. Определители

Рассмотрим таблицу из четырех чисел:

А =

Такая таблица называется квадратной матрицей порядка два. Матрица А имеет две строки и два столбца. Числа ,,,называютсяэлементами матрицы.

Определителем матрицы А называется число

(1)

Пример 1.

Рассмотрим квадратную числовую матрицу

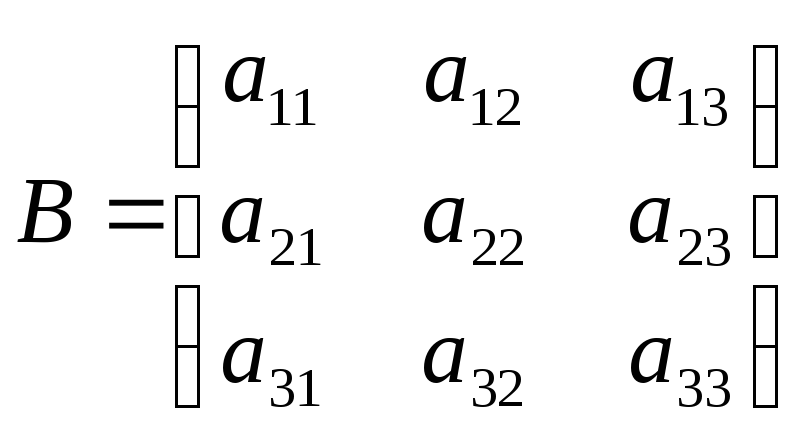
порядка три. Элементы матрицы В имеют два индекса, первый соответствует строке, в которой стоит этот элемент, а второй – столбцу.

Определителем матрицы Вназывается число

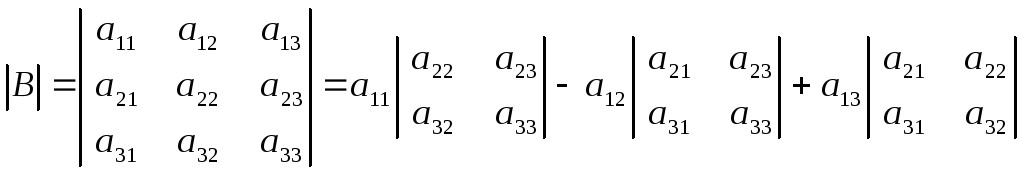(2)

Как вычислять определители 2-го порядка известно.

Пример 2.

Приведем некоторые свойства определителя второго порядка.

1^о. Если получаем иззаменой строк столбцами, то. Действительно, в силу (1)

Замечание 1.Из этого свойства вытекает, что всякое утверждение о строках определителя справедливо и для его столбцов.

2^о. Если матрица D получена из матрицы А перестановкой двух строк, то .

В самом деле,

3^о. Если матрица А имеет две одинаковые строки, то .

4^о. Общий множитель всех элементов строки определителя можно выносить за знак определителя:

Данное свойство проверяется путем раскрытия определителя.

5^о. Если какая-либо строка матрицы А состоит из нулей, то . Это свойство следует из предыдущего приk=0.

6^о. Если матрица D получается из А прибавлением к элементам какой-либо строки соответствующих элементов другой, умноженных на одно и то же число, то , т.е.

Проверьте!

Свойства 1-6 сохраняются и для определителей третьего порядка. Это можно доказать простой проверкой, используя формулу (2).

Обозначим через определитель матрицы, которая получается из В вычеркиванием-ой строки и-ого столбца. Определительназываетсяминором определителя матрицы В, отвечающим элементу . Далее,называетсяалгебраическим дополнением элемента в. Например,

, ,,

, ,

Таким образом по формуле (2)

(3)

Формула (3) дает разложение определителя 3-го порядка по элементам первой строки. Оказывается, что справедливы следующие свойства определителя 3-го порядка, которые можно доказать простыми вычислениями.

7^о. Определитель равен сумме попарных произведений элементов какой – либо строки (или столбца) на их алгебраические дополнения.

8^о. Сумма произведений, какой – либо строки (или столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (или столбца) равна нулю.

Например,

Замечание 2.Если в определителе какая – то строка (столбец) состоит из нулей, то он равен нулю по свойству 5. В противном случае, рекомендуется разлагать его по строке (столбцу), которая имеет только один ненулевой элемент. Если такой строки (столбца) нет, то ее можно получить, используя свойство 6.

Пример 3. Вычислить

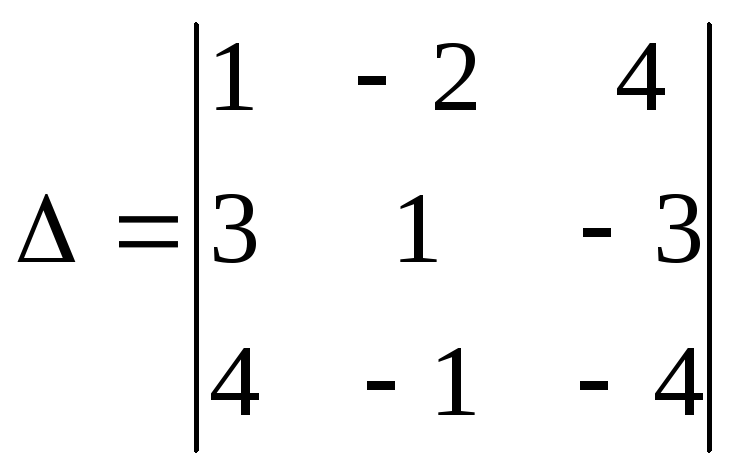
Умножим первую строку на (-3) и прибавим ко второй. Затем первую строку умножим на (-4) и прибавим к третьей. Получим:

.

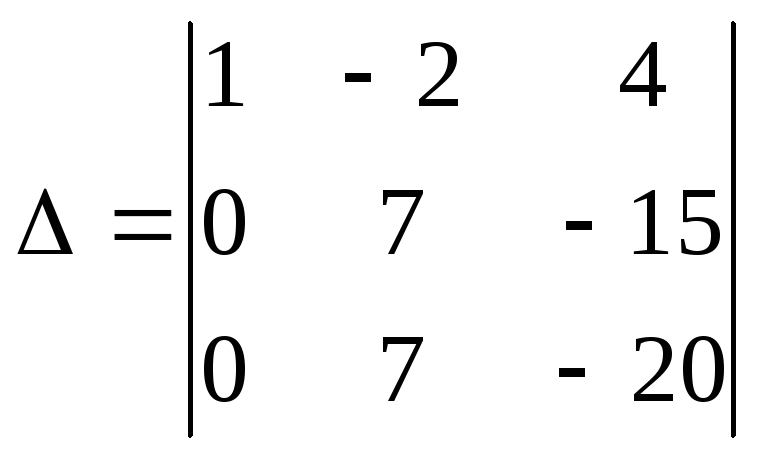Разлагая по 1-му столбцу, находим

.

Пусть теперь дана квадратная матрица порядка :

.

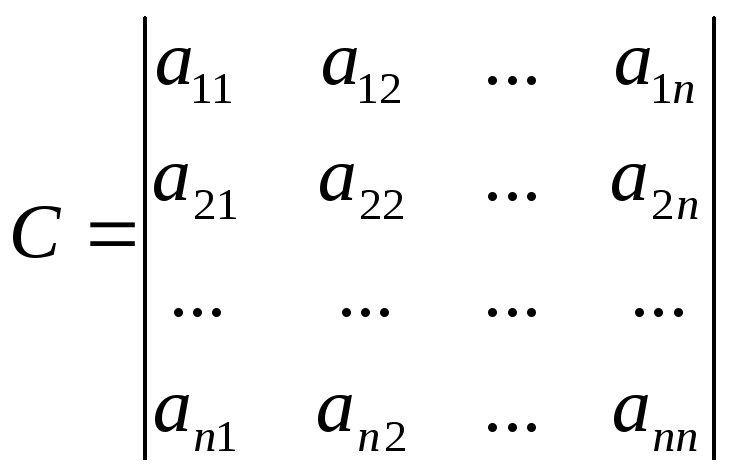По аналогии с формулой (3) полагаем

, (4)

где ;- определитель матрицы порядка, которая получается из С вычеркиванием 1-ой строки и-го столбца. Таким образом, определитель 4-го порядка сводится к определителям 3-го порядка, определитель 5-го порядка сводится к определителям 4-го порядка и т.д.

Свойства 1 – 8 сохраняются и для определителей -го порядка.

Лемма. Определитель треугольной матрицы равен произведению диагональных элементов, т.е.

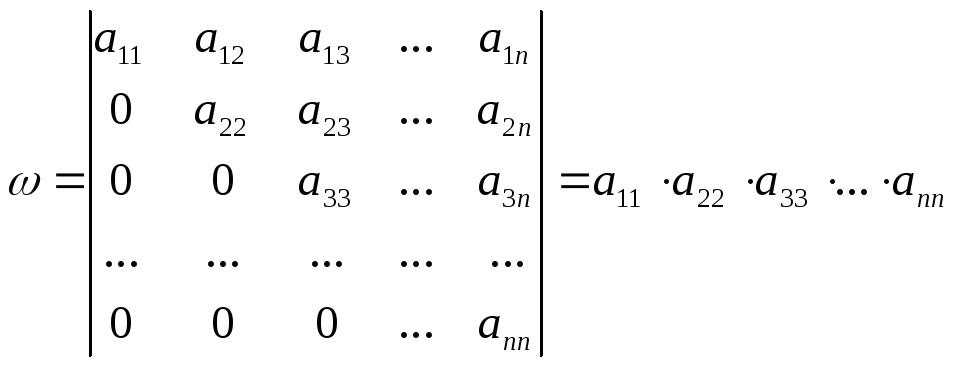(5)

Доказательство ведем индукцией по . Если, то

и формула (5) справедлива. Пусть лемма верна для определителей порядка n-1 (индуктивное предположение). Разлагая (свойство7) определитель порядкаn по первому столбцу, получим

Остается применить индуктивное предположение.

В некоторых случаях, используя свойство 6, удается свести определитель -го порядка к определителю вида (5).

Пример 4. Вычислить определитель порядка :

.

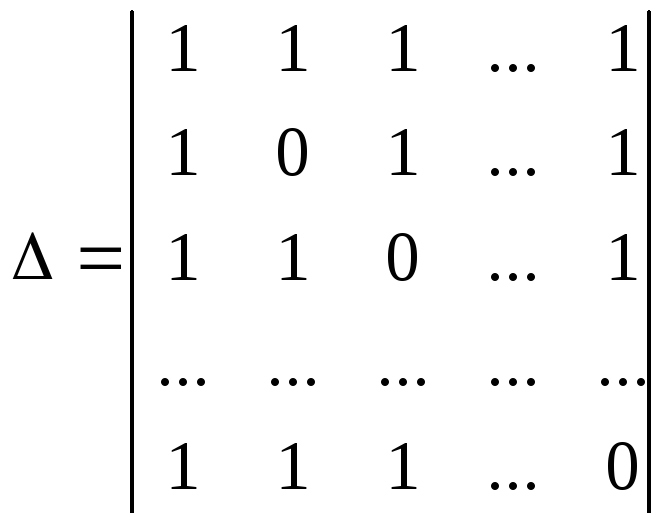Умножим первую строку на (-1) и прибавим ко всем остальным.

Тогда

В силу леммы .