Задача 1

Информация по фирме о нормах затрат ресурсов на единицу выпускаемой продукции, лимитах на эти ресурсы и ценах реализации готовой продукции представлена в таблице.

Наименование ресурсов	Норма затрат на		Объем ресурса
	Продукт А	Продукт В
Сырье (кг)	4	1	329
Оборудование (ст.час.)	1	5	372
Трудоресурсы (чел.час.)	8	1	995
Цена реализации (руб.)	257	259

Требуется:

1. Составить модель расчета оптимальной производственной программы для этой фирмы на основе задачи линейного программирования.

2. Используя графический метод решения этой модели, найти оптимальную программу выпуска продукции, максимизирующую ожидаемый объем продаж.

3. Сформировать задачу, двойственную к задаче расчета оптимальной производственной программы и составить обе группы условий “дополняющей нежесткости”.

4. Подставив в условия “дополняющей нежесткости” оптимальную программу выпуска, найти предельную эффективность имеющихся у предприятия объемов ресурсов.

5. Выполнить проверку оптимальных решений прямой и двойственной задачи подстановкой их в ограничения и целевые функции.

Решение

1. Пусть х₁ – количество выпускаемого продукта А;

х₂ – количество выпускаемого продукта В.

Искомая производственная программа X = (x₁; x₂) выпуска изделий А и В должна удовлетворять всем ресурсным ограничениям. Запишем их в математической форме.

4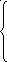х₁ + 1х₂ < 329

1x₁ + 5x₂ < 372

8x₁ + 1x₂ < 995

x₁ > 0, x₂ > 0

Пусть z – выручка от продажи продуктов А и В. Задача состоит в таком выпуске продукции X = (x₁; x₂), который обеспечивает максимальную выручку, т.е. z = 257 x₁ + 259 x₂  max

2. Построим область допустимых решений (ОДР). Запишем уравнения граничных прямых для каждого из неравенств и по две точки на этих прямых.

4х₁ + 1х₂ = 329 (1) 1x₁ + 5x₂ = 372 (2) 8x₁ + 1x₂ = 995 (3)

x1	0	82,25		x1	0	372		x1	0	124,375
x2	329	0		x2	74,4	0		x2	995	0

При подстановке точки (0; 0) в левую часть неравенств они будут выполняться. Следовательно, искомые полуплоскости будут располагаться слева (ниже) граничных прямых. Получим ОДР в результате пересечения всех полуплоскостей в первом квадранте.

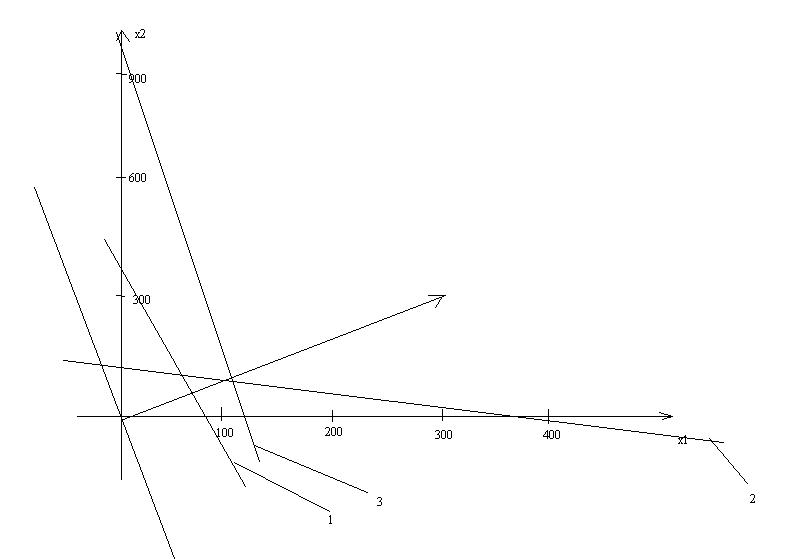
Находим градиент функции:

grad r = (dz/dx₁; dz/dx₂) = (257; 259)

Двигая линии уровня 257х₁ + 259х₂ = h вдоль вектора нормали, находим точку касания линии уровня и ОДР. Это и есть точка максимума функции z. В нашей задаче точка максимума X* лежит на пересечении граничных прямых (2) и (1). Находим ее координаты из системы:

1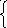х₁ + 5х₂ = 372

4x₁ + 1x₂ = 329

x₁ = 67

x₂ = 61

Оптимальная производственная программа X* = (67; 61) состоит в выпуске 67 изделий А и 61 изделий В. Ожидаемая выручка от их продажи:

z* = 257 * 67 + 259 * 61 = 33018 руб.

3. Исходная задача:

u₁  4х₁ + 1х₂ < 329

u₂  1x₁ + 5x₂ < 372

u₃  8x₁ + 1x₂ < 995

x₁ > 0, x₂ > 0

z = 257 x₁ + 259 x₂  max

Двойственная задача:

4u₁ + 1u₂ + 8u₃  257

1u₁ + 5u₂ + 1u₃  259

u₁  0, u₂  0, u₃  0

w = 329u₁ + 372u₂ + 995u₃  min

Для того, чтобы допустимое решение X исходной задачи и допустимое решение U двойственной задачи были оптимальными, необходимо и достаточно, чтобы выполнялись следующие условия.

x_j * v_j = 0

u_j * y_j = 0

где v_j = a_iju_i – c_j, y_j = b_i - a_ij*x_j

Подставив найденные компоненты вектора X* = (67; 61) в условия получаем:

x₁ * v₁ = 0; x₁ = 67  v₁ = 0 4u₁ + 1u₂ + 8u₃ = 257

x₂ * v₂ = 0; x₂ = 61  v₂ = 0 1u₁ + 5u₂ + 1u₃ = 259

u₁ * y₁ = 0; y₁ = 329 – 4*67 – 1*61 = 0  u₁  0

u₂ * y₂ = 0; y₂ = 372– 1*67 – 5*61 = 0  u₂  0

u₃ * y₃ = 0; y₃ = 995 – 8*67 – 1*61=398  u₃ = 0

Получаем систему уравнений:

4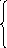u₁ + 1u₂ + 8u₃ = 257 u₁* =54

1u₁ + 5u₂ + 1u₃ = 259 u₂* = 41

u₃ = 0 u₃* = 0

Значение целевой функции двойственной задачи на этом решении:

w* = 329*54 + 372*41 + 995*0 =33018 руб.

Получены следующие результаты расчета модели:

x* = (67; 61); u* = (54; 41; 0)

z* = w* = 33018 руб.

Переменная u_i характеризует абсолютный прирост оптимизируемого показателя z в случае увеличения объема i-го ресурса на одну единицу.

Переменная y_j показывает, сколько остается i-го ресурса после выполнения производственной программы X.

Переменная v_j интерпретируется как возможный убыток по полезности при выпуске j-го продукта.

Оценка u_i* = 54 руб/кг показывает, что если объем сырья увеличить на 1 кг, то при прочих равных условиях максимальная выручка увеличится на 54 руб., а если уменьшить на 1 кг, то снизится на 54 руб.

Оценка u₂* = 41 руб/ст.час. показывает, что если оборудование увеличить на 1 ст.час то при прочих равных условиях максимальная выручка увеличится на 41 руб., а если уменьшить на 1 ст.час, то снизится на 41 руб.

Оценка u₃* = 0 руб/чел.час. показывает, что трудоресурса является избыточным. Уменьшение (в пределах интервала устойчивости) или увеличение фонда времени на трудоресурсы не повлияет на величину ожидаемой выручки.

.

Задача 2

Учитывая данные задания 1, исследовать динамику предельной эффективности сырья при изменении его объема от нуля до бесконечности при сохранении других ресурсов в прежних объемах.

Требуется:

1. Рассмотреть модель расчета оптимальной производственной программы как задачу линейного программирования с параметром, выражающим объем сырья.

2. Используя графический метод решения прямой задачи при увеличении параметра от нуля до бесконечности и условия "дополняющей нежесткости", вычислить убывающие значения предельной эффективности и определить диапазоны их устойчивости.

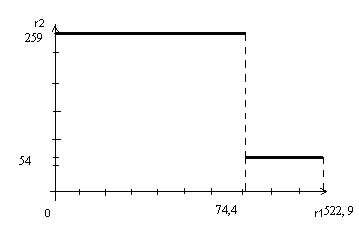
3. Записать выявленную функцию предельной эффективности сырья в табличной форме и построить ее график.

Решение

Проведем на графике прямую (1’), соответствующую минимальному объему сырья, при котором оптимальные двойственные оценки ресурсов остаются равными U* = (54; 41; 0). Также проведем прямую (1’’), соответствующую максимальному при этом же условии объему сырья (верхняя граница интервала устойчивости).

Сырьё.

Найдем объемы сырья r₁’ и r₁’’, соответствующие этим прямым.

Прямая (1’) проходит через точку пересечения прямой (2) с осью Ох₂.

r₁’ = 4*0 + 1*74,4= 74,4 кг

Прямая (1’’) проходит через точку пересечения прямой (3) и (2):

r₁’’ = 4*118,03 + 1*50,8 = 522,9 кг

r₁  [74,4; 522,9]

Допустимое уменьшение объемов сырья:

329 – 74,4 = 254,6

Допустимое увеличение объемов сырья:

522,9 – 329 = 193,9

Найдем функции предельной полезности сырья

При малом r₁ > 0 сырье будет лимитирующим ресурсом и предприятие будет производить только продукт В.

Следовательно,

х₁ = 0  v₁  0

х₂ > 0  v₂ = 0

u₁ > 0

u₂ = 0

u₃ = 0

Получаем систему уравнений:

1u₁ + 5u₂ + 1u₃ = 259

u₂ = 0

u₃ = 0

Из нее находим:

u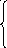₁* = 259

u₂* = 0

u₃* = 0

Эти двойственные оценки будут оптимальными, пока объемы сырья не вырастут до уровня (а₁), т.е. пока объемы сырья не станут равными: r₁ = 259 кг.

При r₁ > 259 оптимальным решением будет точка пересечения прямых (1) и (3), при котором u* = (54; 41; 0), т.е. u₁(r₁) = 54 руб/кг при r₁  [74,4; 522,9].

При r₁ > 259 кг (выше прямой (а₂)), сырье станет избыточным. Поэтому, u₁(r₁) = 0 руб/кг при r₁  [522,9; ].

При r₁  [0; 74,4], z = 259*r₁. При r₁ = 74,4, z = 259 * 74,4 = 19269,6 руб.

При r₁  [74,4; 522,9], z = 19269,6+ 54 (r₁ – 74,4) = 15252 + 54r₁.

При r₁ = 522,9, z = 15252 + 54*522, 9 = 43488,6.

При r₁  [522,9; ], z = 43488,6 руб.

Представим полученные результаты в виде таблицы.

r1 (кг)	[0; 74,4]	[74,4; 522,9]	[522,9; ]
u1(r1) (руб/кг)	259	54	0
z(r1) (руб)	259r1	15252 + 54r3	43488,6

График функции предельной полезности сырья.