
- •Классическое определение вероятности.
- •Формула сложения вероятностей.
- •Формула полной вероятности.
- •Повторные независимые испытания
- •Формула Бернулли
- •1.10. Теоремы Муавра-Лапласа
- •13.Случайные величины: дискретные и непрерывные случайные дискретные величины
- •Пуассона распределение
- •Свойства
- •Свойства
- •Гипергеометрическое распределение.
- •1. Дискретная случайная величина, закон и функция распределения
- •2. Числовые характеристики дискретных случайных величин
- •30. Система случайных величин, закон распределения вероятностей дискретной двумерной случайной величины.
- •31. Функция распределения двумерной случайной величины, ее свойства.
- •Свойства функции распределения двумерной случайной величины
- •Определение плотностей вероятности составляющих двумерной случайной величины:
- •Понятие ковариация и коэффициента корреляции
- •41. Линейная регрессия. Линейная корреляция. Нормальная корреляция
- •42.Закон больших чисел. Лемма Чебышева.
- •43.Неравенство Чебышева.
- •44.Теорема Чебышева.
- •45.Теорема Бернули.
- •46. Центральная предельная теорема.
- •47. Основные понятия математической статистики: вариационный ряд, его характеристики.
- •48. Средние величины, показатели вариации.
- •50. Понятие оценки параметров.
- •51. Методы нахождения оценок: метод моментов, метод максимального правдоподобия, метод наименьших квадратов.
- •52. Понятие статической гипотезы и схеме ее проверки.
- •56.Проверка гипотезы о законе распределения. Хи-квадрат критерий Пирсона.
- •57.Проверка гипотезы о законе распределения. Критерий Колмогорова.
- •58.Проверка гипотезы о законе распределения. Критерий Колмогорова-Смирнова.
41. Линейная регрессия. Линейная корреляция. Нормальная корреляция
Линейная регрессия занимает в технике и теории корреляции особое место. Она обусловлена двумерным нормальным законом распределения СВ Х и Y:
 ,
где
,
где
а0и а1– коэффициенты регрессии,
х – независимая случайная величина.
Рассмотрим двумерную случайную величину (X, Y). Если обе функции регрессии У на X и X на У линейны, то говорят, что X и Y связаны линейной корреляционной зависимостью. Очевидно, что графики линейных функций регрессии — прямые линии, причем можно доказать, что они совпадают с прямыми среднеквадратической регрессии. Имеет место следующая важная теорема. Теорема. Если двумерная случайная величина (X, Y) распределена нормально, то X и Y связаны линейной корреляционной зависимостью.
42.Закон больших чисел. Лемма Чебышева.
Закон
больших чисел Чебышева. Имеет
место следующее утверждение. Пусть![]() -
последовательность попарно независимых
случайных величин, имеющих ограниченные
в совокупности дисперсии, т. е.
-
последовательность попарно независимых
случайных величин, имеющих ограниченные
в совокупности дисперсии, т. е.![]() для
любого i. Тогда, каково бы нибыло
для
любого i. Тогда, каково бы нибыло![]() ,
справедливо соотношение
,
справедливо соотношение
|
|
(54) |
Доказательство: Обозначим
через ![]() величину
величину![]() ,
т.е. среднюю арифметическую n случайных
величин. Случайная величина
,
т.е. среднюю арифметическую n случайных
величин. Случайная величина![]() имеет
математическое ожидание
имеет
математическое ожидание
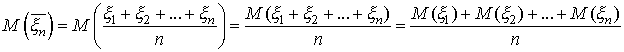
и дисперсию
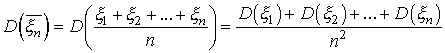
(здесь
мы воспользовались свойствами
математического ожидания и дисперсии).
Применяя к случайной величине ![]() вторую
лемму Чебышева,
найдем, что
вторую
лемму Чебышева,
найдем, что
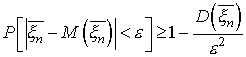
т.е.
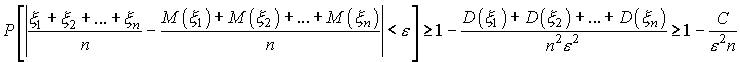
так
как ![]() при
любом i, и следовательно,
при
любом i, и следовательно,
![]()
Учитывая, что вероятность любого события не превосходит единицы, получим
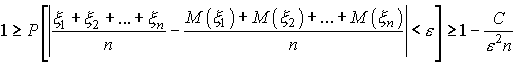
Переходя
к пределу при ![]() ,
имеем
,
имеем
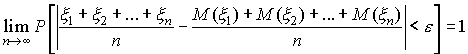
43.Неравенство Чебышева.
Рассмотрим
случайную величину X с конечным мат.
ожиданием и дисперсией
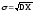
Для любого неотрицательного числа t вероятность наступления события

Пусть Z - непрерывная случайная величина с плотностью вероятности f(Z). Пространство событий величины Z (0; ). Тогда имеет место неравенство
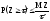
Доказать неравенства
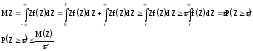
Рассмотрим два сложных события
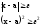
a - произвольное действительное число.
Показать самим, что x - удовлетворяет и одному и другому неравенству.
Тогда
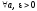 справедливо
справедливо
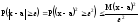
В
данном случае
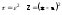
Равномерность неравенств при >0
|
|
|
или, в частности, при a==MX
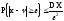
при =t справедливо неравенство Чебышева.
44.Теорема Чебышева.
|
Теорема: При достаточно большом числе независимых опытов среднее арифметическое полученных в опытах значений случайной величины X сходится по вероятности к ее математическому ожиданию
|
Доказательство: Применим
неравенство Чебышева для случайной
величины ![]()
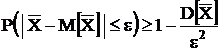 ,
где
,
где 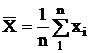 ,
, ![]() ,
, ![]() .
Тогда
.
Тогда
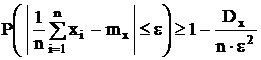 .
.
При любом сколь угодно малом значении ε можно всегда подобрать n такое, чтобы сделать δ значительно меньше единицы.
45.Теорема Бернули.
Рассмотрим систему независимых испытаний Бернулли.
![]()
Система испытаний неограниченна. С каждым i-видом испытаний свяжем дискретную величину Xi
![]()
Хi принимают значения 1, если в i-том испытании произошло событие А и 0 - в противном случае
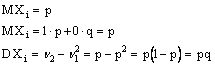
Рассмотрим
случайную величину![]() -
число появлений события А в n испытаниях
-
число появлений события А в n испытаниях
![]()
Рассмотрим
случайную величину ![]()
Это частость наступления события А в n испытаниях
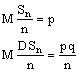
Используем неравенство Чебышева
![]()
где e - произвольное неотрицательное число
Рассмотрим ![]()
Получена теорема Бернулли.
Частость наступления произвольного события при числе испытаний стремящемся к бесконечности по вероятности сходится к теоретической вероятности наступления события.

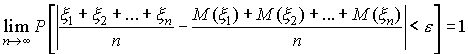
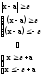
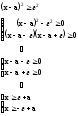
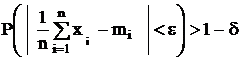 ,
где
d,e - сколь угодно малые
величины; при n®¥ будет выполняться
данное неравенство.
,
где
d,e - сколь угодно малые
величины; при n®¥ будет выполняться
данное неравенство.