Понятие ковариация и коэффициента корреляции

 

Ковариация и коэффициент корреляции позволяют оценить степень зависимости составляющих X и Y двумерной случайной величины (XY).

Ковариацией или корреляционным моментом случайных величинX  и Y называют математическое ожидание произведения отклонений этих величин:

                                            (9.32)

Свойства ковариации

1.     Ковариация двух независимых случайных величин равна нулю.

2.     Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение их математических ожиданий:

       (9.33)

3.     Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений:

     (9.34)

Для вычисления ковариации дискретных величин можно пользоваться выражением:

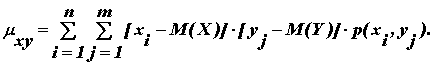                 (9.35)   

Для вычисления ковариации непрерывных величин пользуются выражением:

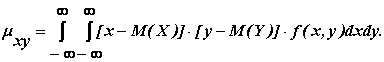                           (9.36)

Ковариация характеризует не только степень зависимости случайных величин, но и их разброс (рассеяние), кроме этого ковариация размерная величина. Ее размерность определяется произведением размерностей случайных величин X и Y. Это затрудняет использование ковариации для оценки степени зависимости случайных величин.     

Этих недостатков не имеет коэффициент корреляции.

Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих величин:

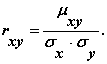                                                                                      (9.37)

Свойства  коэффициента корреляции

1.     Коэффициент    корреляции    принимает    значения  на  отрезке

     [-1;1], т.е.:

                             

2.     Если случайные величины независимы, то их коэффициент корреляции равен нулю. Случайные величины, коэффициент корреляции которых равен нулю,  называют некоррелированными.

     Из независимости случайных величин следует их         некоррелированность, но обратное, в общем случае, неверно.

3.     Если коэффициент корреляции двух случайных величин равен                                                                  по абсолютной величине единице, то между этими случайными величинами существует линейная функциональная связь.

32. Корреливанность и зависимость случайных величин.

Две случайные величины X и У называют коррелированными, если их корреляционный момент (или, что то же, коэффициент корреляции) отличен от нуля; X и У называют некоррелированными величинами, если их корреляционный момент равен нулю. 

Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю.  Две коррелированные величины также и зависимы. Для того чтобы доказать некоррелированность X и У, достаточно убедиться в том, что µ_xy=0. Найдем корреляционный момент по формуле

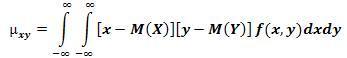
Итак, из коррелнрованности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

32. Линейная регрессия.

Линейная регрессия занимает в технике и теории корреляции особое место. Она обусловлена двумерным нормальным законом распределения СВ Х и Y:

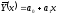, где

а₀и а₁– коэффициенты регрессии,

х – независимая случайная величина

Параметры уравнения регрессии определяются методом наименьших квадратов, предложенным Лагранжем и Гауссом, который сводится к следующему.

Строятся квадратичные формы:

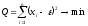
x_i – измеренное значение переменной,

e- истинное или теоретическое значение этой величины.

Требуется, чтобы сумма квадратов отклонений измеренных значений относительно истинных была минимальна.

В случае линейной регрессии за теоретическое значение принимается значение 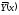, т.е. ищется такая прямая линия с коэффициентами а₀и а₁, чтобы сумма квадратов отклонений от этой линии была минимальна.

,

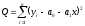у_i– измеренное значение переменнойY.

Минимальные квадратичные формы получают, приравнивая к нулю ее производные по а₀и а₁:

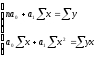
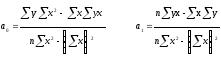
32. Нормальный закон распределения на плоскости.

На практике часто встречаются двумерные случайные величины, распределение которых нормально.  Нормальным законом распределения на плоскости называют распределение вероятностей двумерной случайной величины (X, Y), если

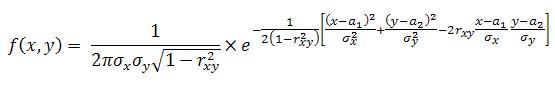
Мы видим, что нормальный закон на плоскости определяется пятью параметрами: а₁, а₂, σ_х, σ_у и r_xу (а₁, а₂ — математические ожидания,σ_х, σ_у — средние квадратические отклонения, r_xу — коэффициент корреляции величин X и У ). Если составляющие нормально распределенной случайной величины некоррелированны, то плотность совместного распределения системы равна произведению плотностей распределения составляющих, а отсюда и следует независимость составляющих. Справедливо и обратное утверждение. Итак, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.