Задание для самостоятельной работы.
Найти точки разрыва следующих функций:
-
23.
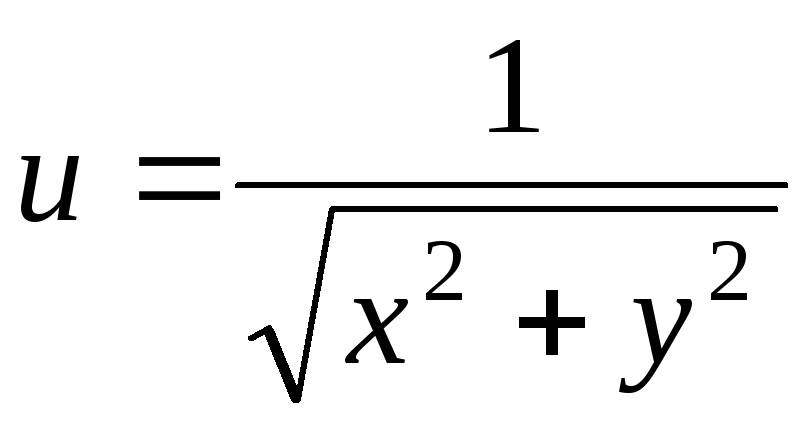.24.
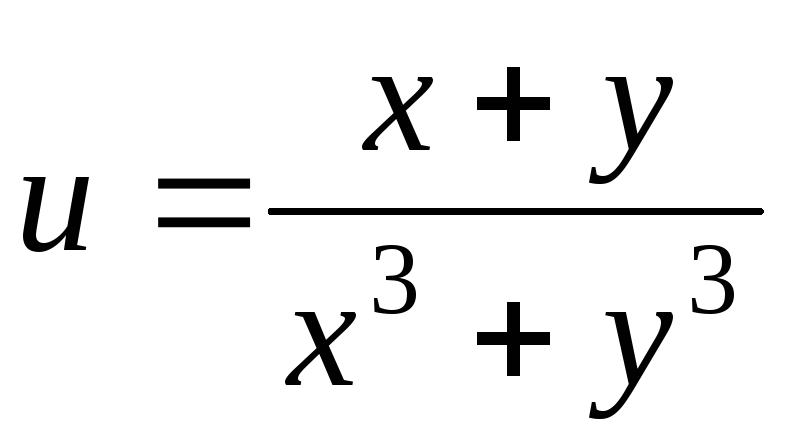.25.
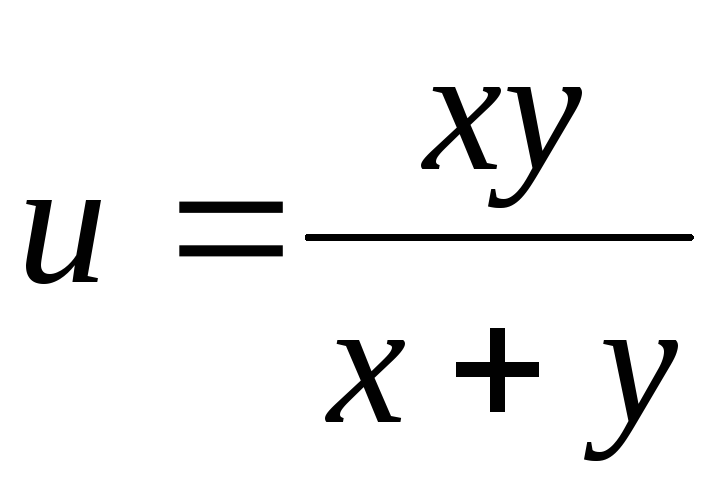.26.
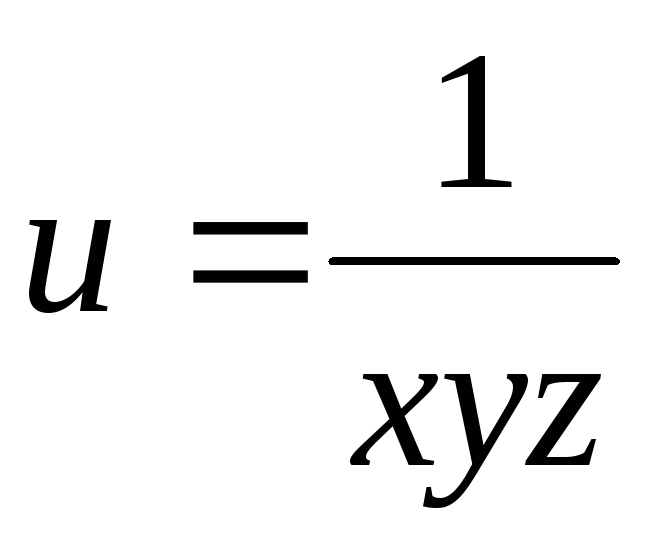.27.
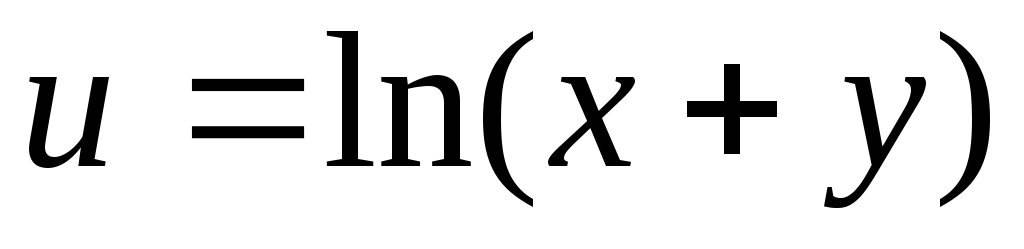.28.
.
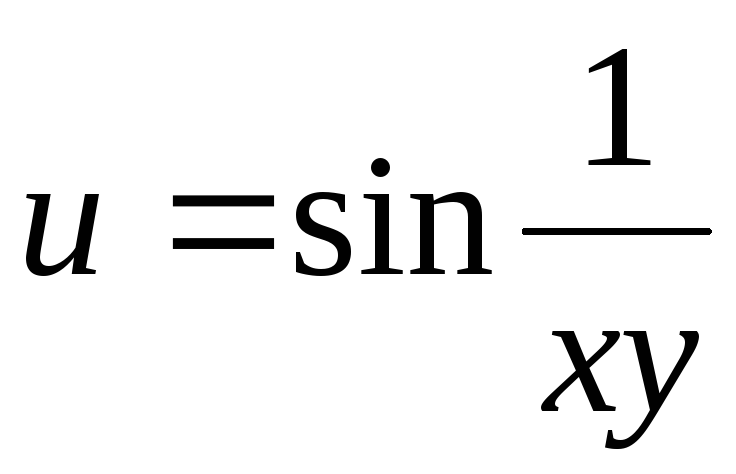29.
Показать,
что функция
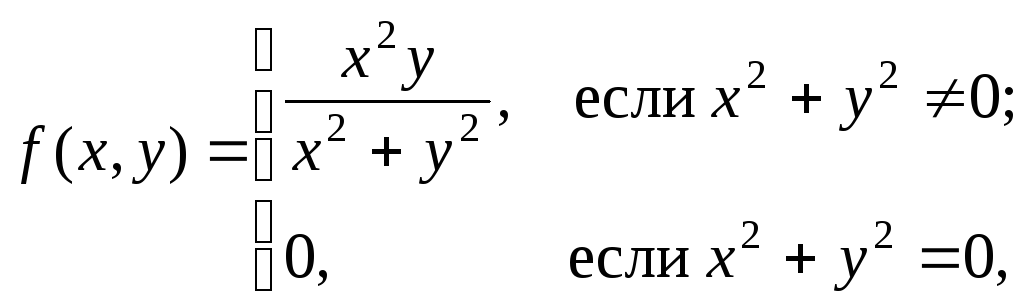в
точке М(0;
0) непрерывна вдоль каждого луча
,
проходящего через эту точку, т.е.
существует
;
однако эта функция не является непрерывной
в точке (0; 0).
Является ли функция
непрерывной в своей области определения?
5. Частные производные функции нескольких переменных
Определение 6. Частной производной по х от функции z = f(х, у) называется предел отношения частного приращения хz по х к приращению х при стремлении х к нулю.
Частная производная по х от функции z = f(х, у) обозначается одним из символов
,
,
,
.
Таким образом, по определению,
.
Аналогично частная производная по у от функции z = f(х, у) определяется как предел отношения частного приращения уz по у к приращению у при стремлении у к нулю. Частная производная по у обозначается одним из символов
,
,
,
.
Таким образом,
.
Заметив, что хz вычисляется при неизменном у, а уz при неизменном х, мы можем определения частных производных сформулировать так: частной производной по х от функции z = f(х, у) называется производная по х, вычисленная в предположении, что у – постоянная. Частной производной по у от функции z = f(х, у) называется производная по у, вычисленная в предположении, что х – постоянная.
Из этого определения ясно, что правила вычисления частных производных совпадают с правилами, указанными для функций одной переменной, и только требуется каждый раз помнить, по какой переменной ищется производная.
Пример
14. Дана
функция
;
требуется найти частные производные
и
.
Решение.
,
.
Пример 15. z = xy.
Здесь
,
.
Частные производные функции любого числа переменных определяются аналогично. Так, если имеем функцию и четырех переменных х, у, z, t:
,
то
,
и
т.д.
Пример
16.
.
,
,
,
.
Геометрическая интерпретация частных производных функции двух переменных
Частная
производная
численно равна тангенсу угла наклона
касательной к кривой, получающейся в
сечении поверхностиz
= f(х,
у)
плоскостью x
= const.
Аналогично
частная производная
численно равна тангенсу угла наклона
касательной к сечению поверхностиz
= f(х,
у)
плоскостью у
= const.
Задания для самостоятельной работы.
Найти
частные производные
,
,
:
-
31.
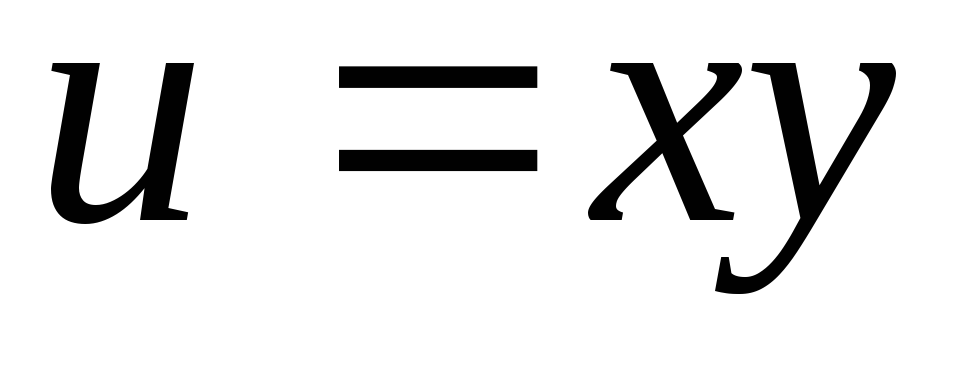.32.
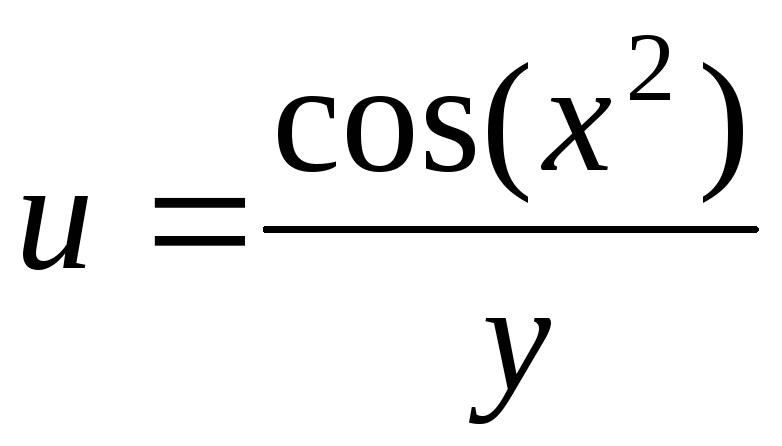.33. u = xy.
34.
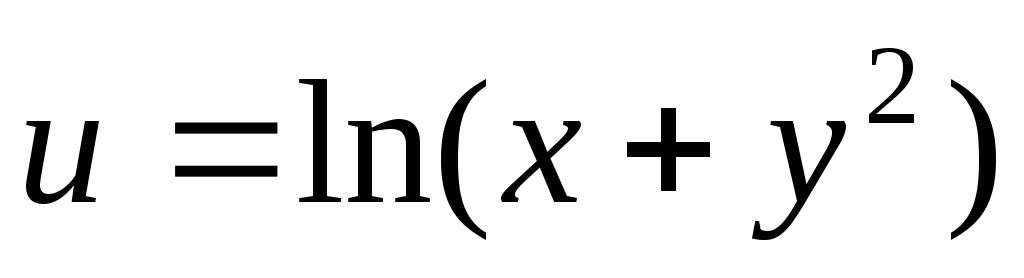.35.
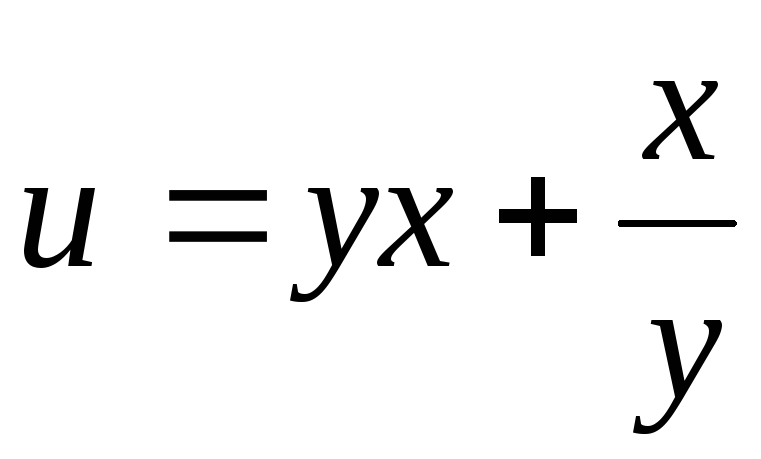.36.
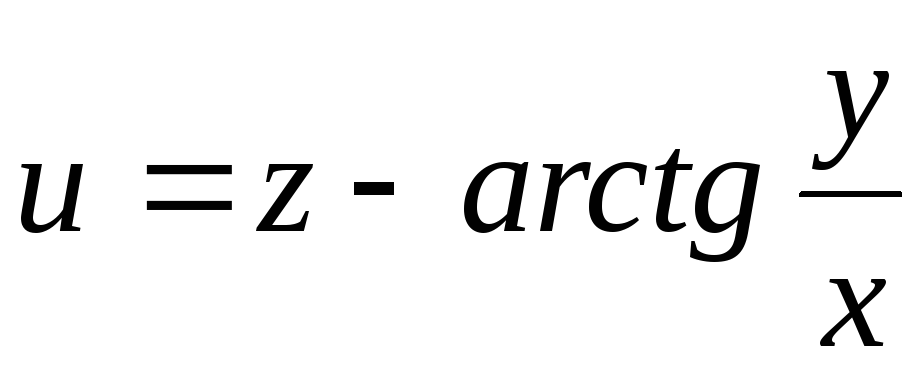.37.
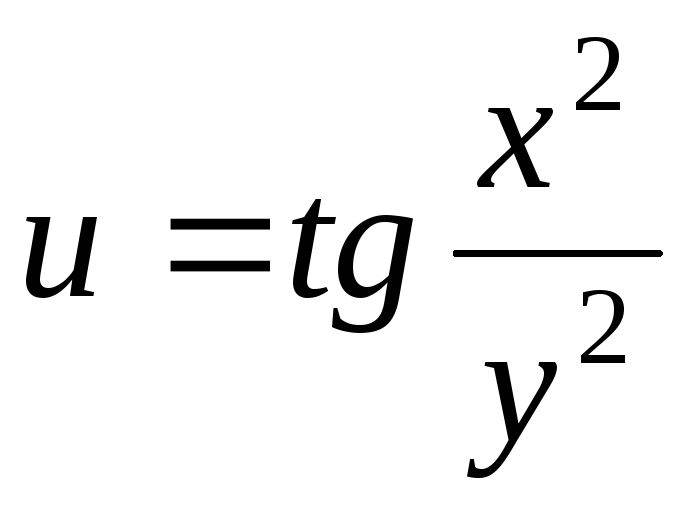.38.
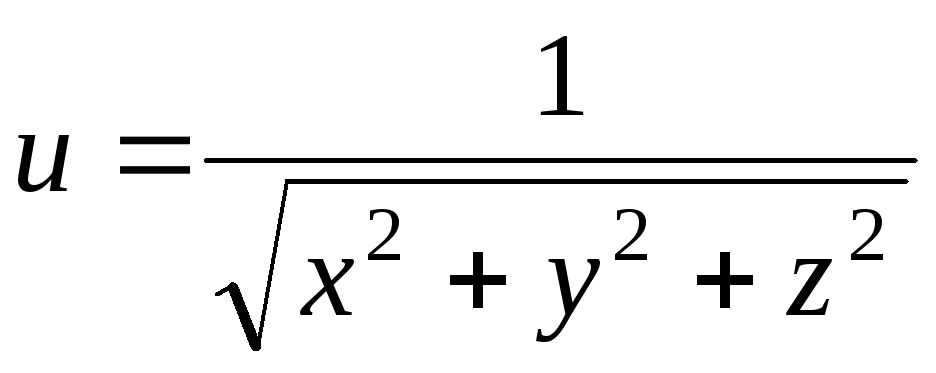.39.
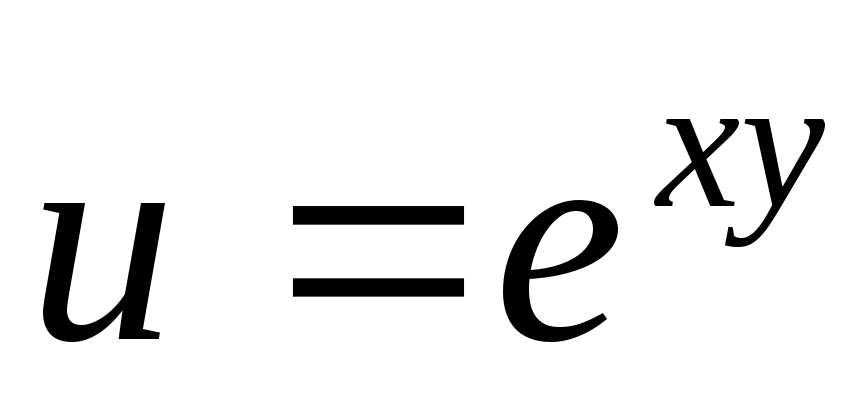.40.
.
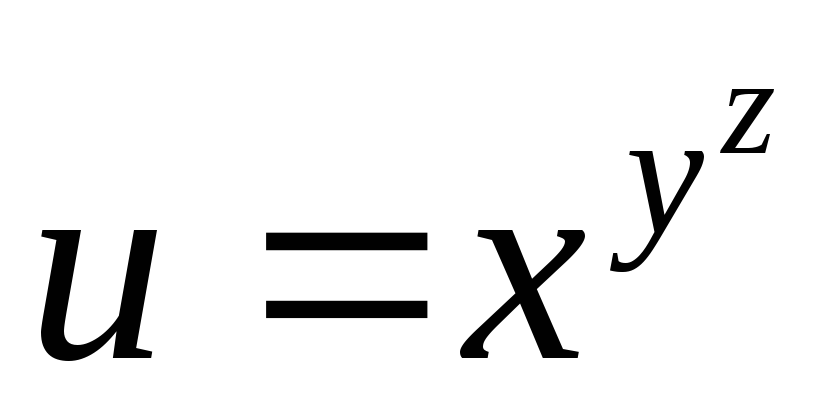6. Полное приращение и полный дифференциал
По определению полного приращения функции z = f(х, у) имеем
.
(5)
Предположим, что f(х, у) в рассматриваемой точке (х, у) имеет непрерывные частные производные.
Выразим z через частные производные. Для этого в правой части равенства (5) прибавим и вычтем f(х, у + у):
.
(6)
Выражение
f(х, у + у) – f(х, у),
стоящее во второй квадратной скобке, можно рассматривать как разность двух значений функции одной переменной у (значение х остается постоянным). Применяя к этой разности теорему Лагранжа, получим
,
(7)
где
заключено междуу
и у
+ у.
Точно так же выражение, стоящее в первой квадратной скобке равенства (6), можно рассматривать как разность двух значений функции одной переменной х (второй аргумент сохраняет одно и то же значение у + у). Применяя к этой разности теорему Лагранжа, получим
,
(8)
где
заключено междух
и х
+ х.
Внося выражения (7) и (8) в равенство (2), получим
.
(9)
Так как, по предположению, частные производные непрерывны, то
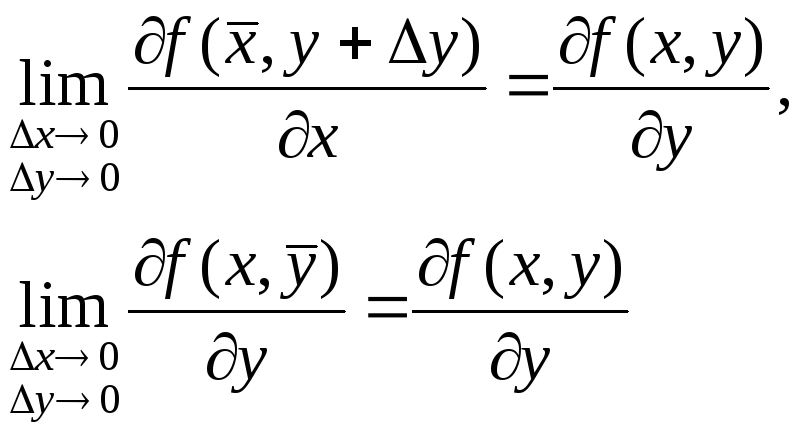(10)
(так
как
и
заключены соответственно междух
и х
+ х,
у
и у
+ у,
то при х
0 и у
0
и
стремятся соответственно кх
и у).
Равенство (10) можно переписать в виде
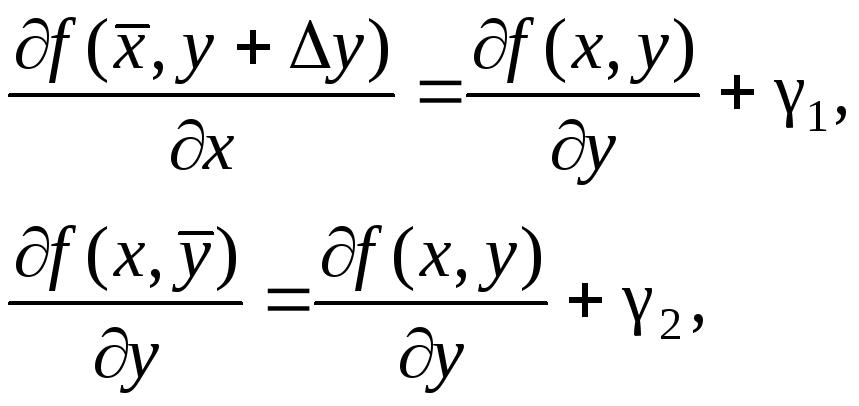(11)
где
величины 1
и 2
стремятся к нулю, когда х
и у
стремятся к нулю (т.е. когда
).
В силу равенства (11) соотношение (9) принимает вид
.
(12)
Сумма
двух последних слагаемых правой части
является бесконечно малой высшего
порядка относительно
.
Действительно, отношение
при
0, так как 1
является бесконечно малой величиной,
а
ограниченной
.Аналогично проверяется,
что
.
Сумма
первых двух слагаемых есть выражение,
линейное относительно х
и у.
При
и
это выражение представляет собойглавную
часть приращения, отличаясь от z
на бесконечно малую высшего порядка
относительно
.
Определение 7.Функция z = f(х, у), полное приращение z которой в данной точке (х, у) может быть представлена в виде суммы двух слагаемых: выражения, линейного относительно х и у, и величины, бесконечно малой высшего порядка относительно , называется дифференцируемой в данной точке, а линейная часть приращения называется полным дифференциалом и обозначается через dz или df.
Из равенства (12) следует, что если функция f(х, у) имеет непрерывные частные производные в данной точке, то она дифференцируема в этой точке и имеет полный дифференциал
.
Равенство
(12) можно переписать в виде
и с точностью до бесконечно малых высшего
порядка относительно
можно написать следующее приближенное
равенство:
z dz. (13)
Приращения независимых переменных х и у мы будем называть дифференциалами независимых переменных х и у иобозначать соответственно через dx и dy. Тогда выражение полного дифференциала примет вид
.
(14)
Таким образом, если функция z = f(х, у) имеет непрерывные частные производные, то она дифференцируема в точке (х, у), и ее полный дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных.
Пример 17. Найти полный дифференциал и полное приращение функции z = ху в точке (2; 3) при х = 0.1, у = 0.2.
Решение.
z = (х + х)(у + у) – ху = ух + ху + ху,
.
Следовательно,
z = 30.1 + 20.2 + 0.10.2 = 0.72, dz = 30.1 + 20.2 = 0.7.
Предыдущие рассуждения и определения соответственным образом обобщаются на функции любого числа аргументов.
Если имеем функцию любого числа переменных
w = f(x, y, z, u, …, t),
причем
все частные производные
,
,
…,
непрерывны в точке (x,
y,
z,
u,
…, t),
то выражение
является
главной частью полного приращения
функции и называется полным
дифференциалом.
Доказательство того, что разность w
dw
является бесконечно малой более высокого
порядка, чем
,
проводится совершенно так же, как и для
функции двух переменных.
Пример
18. Найти
полный дифференциал функции
трех переменныхх,
у,
z.
Решение. Заметив, что частные производные
,
,
непрерывны при всех значениях х, у, z, находим
.