2. Геометрическое изображение функции двух переменных
Рассмотрим функцию
z = f(x, y), (1)
определенную в области G на плоскости Оху (эта область может быть, в частности, и всей плоскостью), и систему прямоугольных декартовых координат Охуz (рис. 1). В каждой точке (х, у) восставим перпендикуляр к плоскости Оху и на нем отложим отрезок, равный f(х, у).
Тогда мы получим в пространстве точку Р с координатами
x, y, z = f(х, у).
Геометрическое место точек Р, координаты которых удовлетворяют уравнению (1), называется графиком функции двух переменных. Из курса аналитической геометрии мы знаем, что уравнение (1) в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух переменных является поверхность, проектирующаяся на плоскость Оху в область определения функции. Каждый перпендикуляр к плоскости Оху пересекает поверхность z = f(x, y) не более чем в одной точке.
z
z
0
P
z
у
у
z
= x2
+ y2
x
G
х
0
у
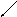
х
Рис.
1
Рис.
2
Пример 10. Графиком функции z = х2 + у2, как известно из аналитической геометрии, является параболоид вращения (рис. 2).
Замечание. Функцию трех и более переменных изобразить с помощью графика в пространстве невозможно.
Задание для самостоятельной работы.
Определить и изобразить область существования следующих функций:
-
1.
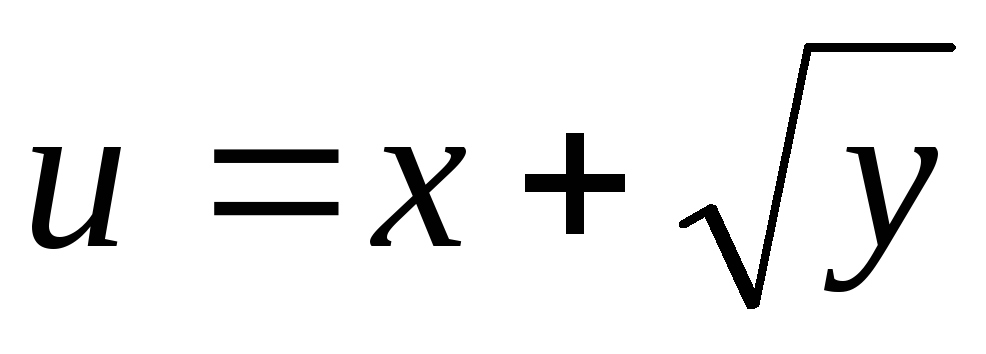.2.
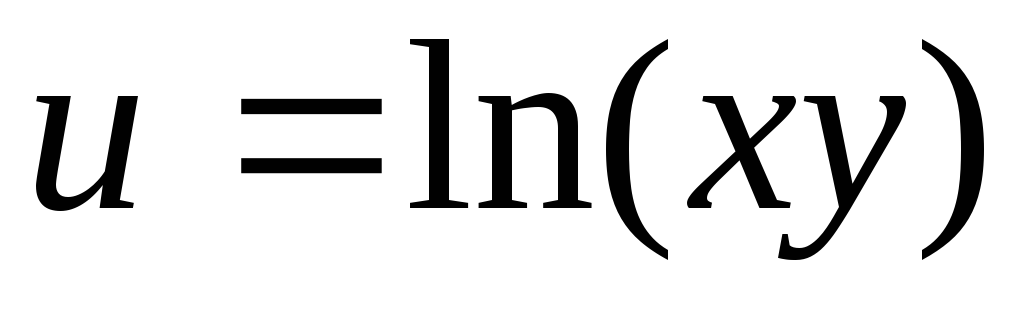.3.
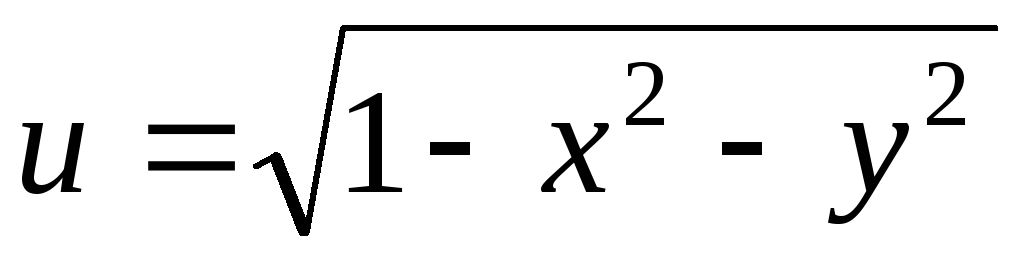.4.
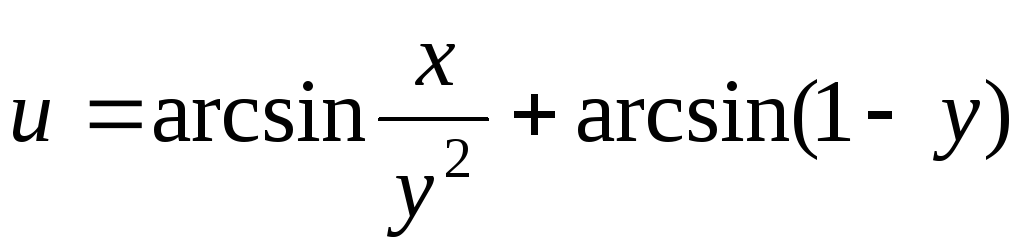.5.
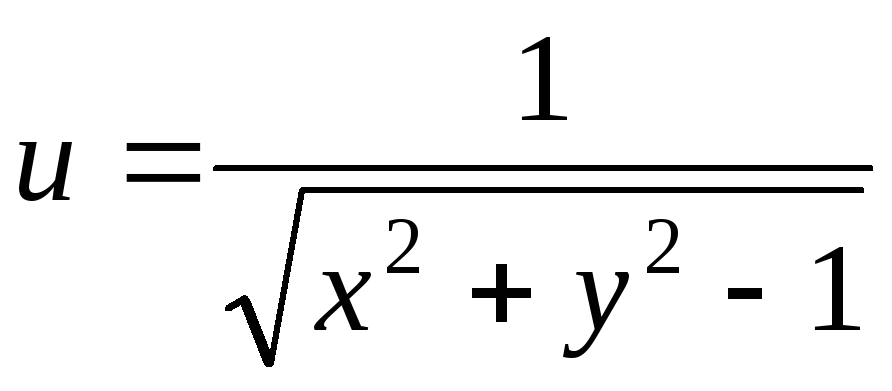.6.
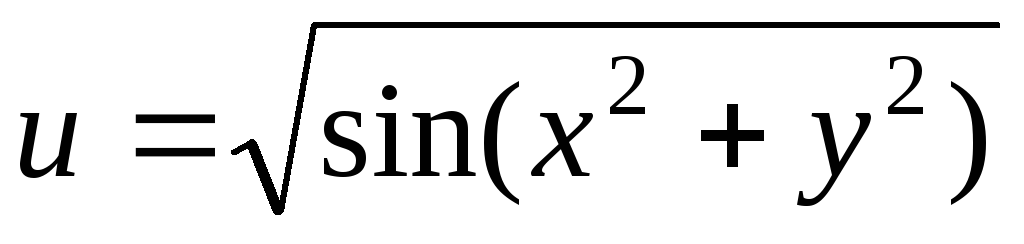.7.
.8.
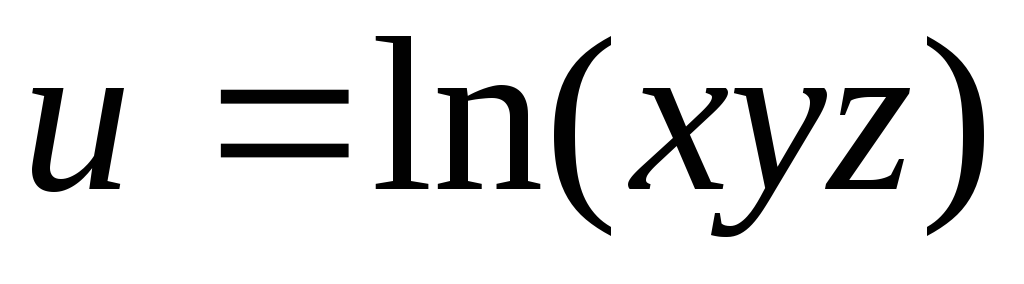.9.
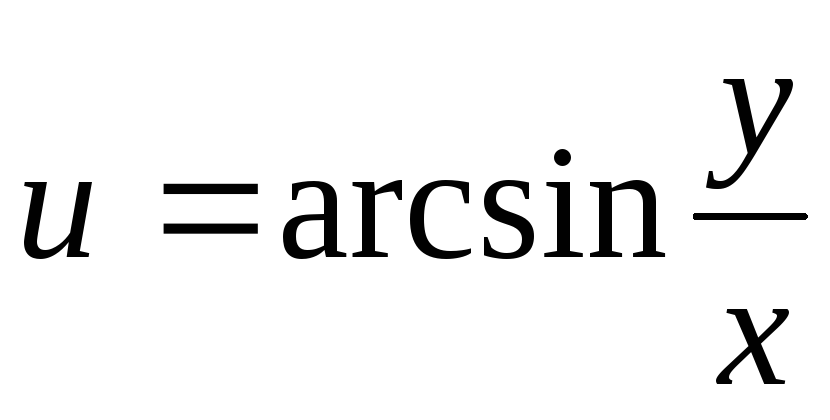.10.
.
3. Частное и полное приращение функции
Рассмотрим линию пересечения поверхности
z = f(x, y)
с плоскостью y = const, параллельной плоскостью Oxz.
Так как в этой плоскости у сохраняет постоянное значение, то z вдоль кривой, у которой у постоянное, будет меняться только в зависимости от изменения х. Дадим независимой переменной х приращение х; тогда z получит приращение, которое называется частным приращением z по х и обозначается через хz, так что
.
Аналогично, если х сохраняет постоянное значение, а у получает приращение у, то z получает приращение, называемое частным приращением z по у. Это приращение обозначают символом уz:
.
Приращение уz функция получает «вдоль линии» пересечения поверхности z = f(х, у) с плоскостью x = const, параллельной плоскости Oyz.
Наконец, сообщив аргументу х приращение х, а аргументу у – приращение у, получим для z новое приращение z, которое называется полным приращением функции z и определяется формулой
.
Надо
заметить, что, вообще говоря, полное
приращение не равно сумме частных
приращений, т.е.
.
Пример 11. z = xy.
;
;
.
При
х
= 1, у
= 2, х
= 0,2, у
= 0,3 имеем
,
,
.
Аналогичным образом определяются частные и полное приращения функции любого числа переменных. Так, для функции трех переменных u = = f(x, y, t) имеем
,
,
,
.