Эллиптический параболоид.

Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:

Рис. 4

где и.

Уравнение (26) называется каноническим уравнением эллиптического параболоида.

Рассмотрим сечения данной поверхности координатными плоскостями и. Получаем соответственно уравнения:

из которых следует, что в сечениях получаются параболы, симметричные относительно оси , с вершинами в начале координат.

Теперь рассмотрим сечения данного параболоида плоскостями , параллельными координатной плоскости. Линия, получающаяся в сечении, определяется уравнениями:

из которых следует, что при плоскость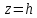пересекает эллиптический параболоид по эллипсу с полуосямии. При увеличениивеличиныитоже увеличиваются; приэллипс вырождается в точку (плоскостькасается данного гиперболоида). Приуравненияопределяют мнимый эллипс, т.е. точек пересечения плоскостис данным гиперболоидом нет.

Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.

Точка называется вершиной параболоида; числаи– его параметрами.

В случае уравнениеопределяет окружность с центром на оси, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).

Гиперболический параболоид.

Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением:

Рис. 5

где .

Уравнение 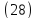называется каноническим уравнением гиперболического параболоида.

Рассмотрим сечение параболоида плоскостью . Получаем уравнение:

из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси , с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости, получаются так же направленные вверх параболы.

рассмотрим сечение данного параболоида плоскостью .

Получаем уравнение:

из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси , с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости, получим уравнения:

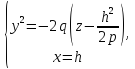
из которых следует, что при любом 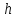в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (29).

Рассмотрим сечения параболоида плоскостями , параллельными плоскости, получим уравнения:

из которых следует, что при в сечении получаются гиперболы, пересекающие плоскость; при– гиперболы, пересекающие плоскости; при– гипербола вырождается в пару пересекающихся прямых:

точка называется вершиной параболоида; числаи– его параметрами.

Конус второго порядка.

Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:

Рис. 6

Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью получаем линию:

распадающуюся на две пересекающиеся прямые:

Аналогично, в сечении конуса плоскостью также получаются две пересекающиеся прямые:

Рассмотрим сечения поверхности плоскостями , параллельными плоскости. Получим:

из которых следует, что при ив сечениях получаются эллипсы с полуосями,. При увеличении абсолютной величиныполуосиитакже увеличиваются.

При линия пересечения поверхности с плоскостьювырождается в точку.