Эллипсоид.

Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:

Рис. 1

Уравнение (20) называется каноническим уравнением эллипсоида.

Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости . Каждая из таких плоскостей определяется уравнением вида , где – любое число, а линия, которая получается в сечении, определяется двумя уравнениями:

Исследуем уравнения (21) при различных значениях .

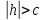
1. Если , то и уравнения (21) определяют мнимый эллипс, т.е. точек пересечения плоскости с данным эллипсоидом не существует.

2. Если , тои линия (21) вырождается в точкии(плоскостикасаются эллипсоида).

3. Если то уравнения (21) можно представить в виде:

откуда следует, что плоскость пересекает эллипсоид по эллипсу с полуосями и. При уменьшениизначенияиувеличиваются и достигают своих наибольших значений при, т. е. в сечении эллипсоида координатной плоскостью получается самый большой эллипс с полуосями и.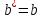

Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям и .

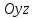Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность. Величины называются полуосями эллипсоида. В случае, эллипсоид является сферой.

Однополостный гиперболоид.

Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:

Рис. 2

Уравнение 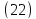называется каноническим уравнением однополостного гиперболоида.

Установим вид поверхности . Для этого рассмотрим сечение ее координатными плоскостями и .Получаем соответственно уравнения:

из которых следует, что в сечениях получаются гиперболы.

Теперь рассмотрим сечения данного гиперболоида плоскостями , параллельными координатной плоскости. Линия, получающаяся в сечении, определяется уравнениями:

из которых следует, что плоскость пересекает гиперболоид по эллипсу с полуосямии, достигающими своих наименьших значений при , т.е. в сечении данного гиперболоида координатной осьюполучается самый маленький эллипс с полуосямии. При бесконечном возрастаниивеличиныивозрастают бесконечно.

Таким образом, рассмотренные сечения позволяют изобразить однополостный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости .

Величины 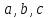называются полуосями однополостного гиперболоида.

Двуполостный гиперболоид.

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:

Рис. 3

Уравнение (24) называется каноническим уравнением двуполостного гиперболоида.

Установим геометрический вид поверхности (24). Для этого рассмотрим его сечения координатными плоскостями и. Получаем соответственно уравнения:

из которых следует, что в сечениях получаются гиперболы.

Теперь рассмотрим сечения данного гиперболоида плоскостями , параллельными координатной плоскости. Линия, полученная в сечении, определяется уравнениями:

из которых следует, что при плоскостьпересекает гиперболоид по эллипсу с полуосямии. При увеличениивеличиныитоже увеличиваются.

При уравнениям (25) удовлетворяют координаты только двух точек:и(плоскостикасаются данной поверхности).

При уравнения (25) определяют мнимый эллипс, т.е. точек пересечения плоскостис данным гиперболоидом не существует.

Величины 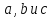называются полуосями двуполостного гиперболоида.