2. Уравнения прямой в пространстве

Прямую в пространстве всегда можно определить как линию пересечения двух непараллельных плоскостей. Если уравнение одной плоскости , уравнение второй плоскости, тогда уравнение прямой задаётся виде

здесь неколлинеарен. Эти уравнения называютсяобщими уравнениями прямой в пространстве.

Канонические уравнения прямой

Любой ненулевой вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Если известна точка прямой и её направляющий вектор, то канонические уравнения прямой имеют вид:

. (9)

Параметрические уравнения прямой

Пусть заданы канонические уравнения прямой

.

Отсюда, получаем параметрические уравнения прямой:

(10)

Эти уравнения удобны при нахождении точки пересечения прямой и плоскости.

Уравнение прямой, проходящей через две точки

Уравнение прямой, проходящей через две точки иимеет вид:

.

Угол между прямыми

Угол между прямыми

и

равен углу между их направляющими векторами. Следовательно, его можно вычислить по формуле (4):

.

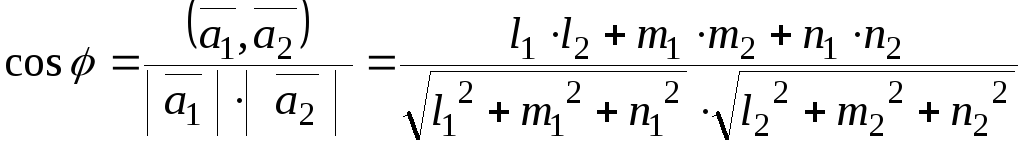Условие параллельности прямых:

.

Условие перпендикулярности плоскостей:

.

Расстояние точки от прямой

Пусть дана точкаи прямая

.

Из канонических уравнений прямой известны точка , принадлежащая прямой,и её направляющий вектор . Тогда расстояние точкиот прямой равно высоте параллелограмма, построенного на векторахи. Следовательно,

.

Условие пересечения прямых

Две непараллельные прямые

,

пересекаются тогда и только тогда, когда

.

Взаимное расположение прямой и плоскости.

Пусть заданы прямая и плоскость. Уголмежду ними можно найти по формуле

.

Задача 73. Написать канонические уравнения прямой

(11)

Решение. Для того чтобы записать канонические уравнения прямой (9), необходимо знать любую точку, принадлежащую прямой, и направляющий вектор прямой.

Найдём вектор , параллельный данной прямой. Так как он должен быть перпендикулярен к нормальным векторам данных плоскостей, т. е.

, , то

.

Из общих уравнений прямой имеем, что ,. Тогда

.

Так как точка любая точка прямой, то её координаты должны удовлетворять уравнениям прямой и одну из них можно задать, например,, две другие координаты найдём из системы (11):

.

Отсюда, .

Таким образом, канонические уравнения искомой прямой имеют вид:

или .

Задача 74. Вычислить расстояние между параллельными прямыми:

и .

Решение. Из канонических уравнений первой прямой известны координаты точки , принадлежащей прямой, и координаты направляющего вектора. Из канонических уравнений второй прямой также известны координаты точкии координаты направляющего вектора.

Расстояние между параллельными прямыми равно расстоянию точки от второй прямой. Это расстояние вычисляется по формуле

.

Найдём координаты вектора .

Вычислим векторное произведение :

.

Тогда

Задача 75. Найти точку симметричную точкеотносительно прямой

.

Решение. Запишем уравнение плоскости перпендикулярной к данной прямой и проходящей через точку . В качестве её вектора нормалиможно взять направляющий вектор прямой. Тогда. Следовательно,

.

Найдём точку точку пересечения данной прямой и плоскости П. Для этого запишем параметрические уравнения прямой, используя уравнения (10), получим

Далее, решим систему, в которую входит уравнение плоскости и параметрические уравнения прямой:

Следовательно, .

Пусть точка симметричная точкеотносительно данной прямой. Тогда точкасередина отрезка. Для нахождения координат точкииспользуем формулы координат середины отрезка:

, ,.

Получим

, ,

.

Итак, .

Задача 76. Написать уравнение плоскости, проходящей через прямую и

а) через точку ;

б) перпендикулярно плоскости .

Решение. Запишем общие уравнения данной прямой. Для этого рассмотрим два равенства:

Это означает, что искомая плоскость принадлежит пучку плоскостей с образующими и её уравнение может быть записано в виде (8):

(12)

а) Найдём ииз условия, что плоскость проходит через точку, следовательно, её координаты должны удовлетворять уравнению плоскости. Подставим координаты точкив уравнение пучка плоскостей:

.

Найденное значение подставим в уравнение (12). получим уравнение искомой плоскости:

б) Найдём ииз условия, что искомая плоскость перпендикулярна плоскости. Вектор нормали данной плоскости, вектор нормали искомой плоскости(см. уравнение пучка плоскостей (12).

Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. Следовательно,

.

Отсюда,

Подставим найденное значение в уравнение пучка плоскостей (12). Получим уравнение искомой плоскости:

Задачи для самостоятельного решения

Задача 77. Привести к каноническому виду уравнения прямых:

1) 2)

Задача 78. Написать параметрические уравнения прямой , если:

1) ,; 2),.

Задача 79. Написать уравнение плоскости, проходящей через точку перпендикулярно прямой

Задача 80. Написать уравнения прямой, проходящей точку перпендикулярно плоскости.

Задача 81. Найти угол между прямыми:

1) и;

2) и

Задача 82. Доказать параллельность прямых:

и .

Задача 83. Доказать перпендикулярность прямых:

и

Задача 84. Вычислить расстояние точки от прямой:

1) ; 2).

Задача 85. Вычислить расстояние между параллельными прямыми:

и .

Задача 86. В уравнениях прямой определить параметртак, чтобы эта прямая пересекалась с прямой и найти точку их пересечения.

Задача 87. Показать, что прямая параллельна плоскости, а прямаялежит в этой плоскости.

Задача 88. Найти точку симметричную точкеотносительно плоскости, если:

1) , ;

2) , ;.

Задача 89. Написать уравнение перпендикуляра, опущенного из точки на прямую.

Задача 90. Найти точку симметричную точкеотносительно прямой.

ОТВЕТЫ