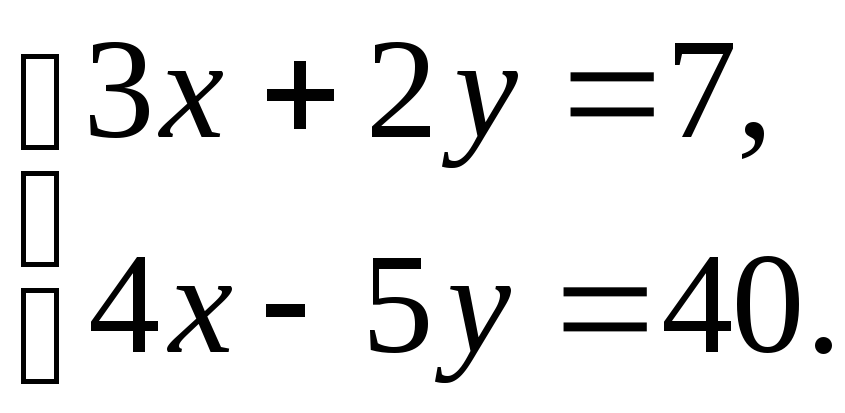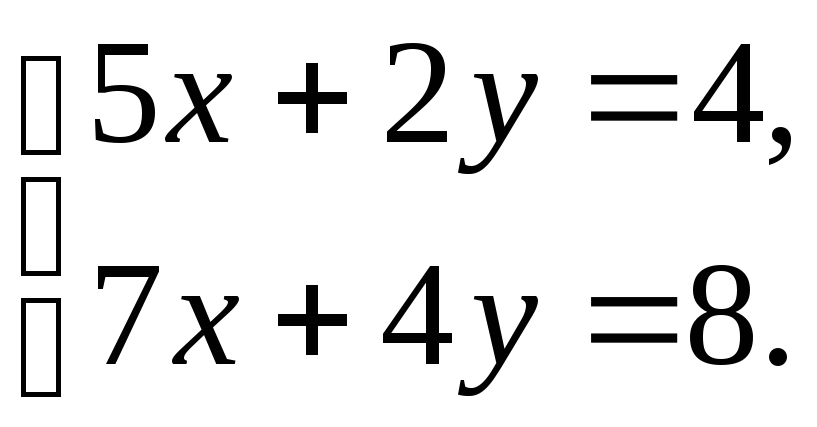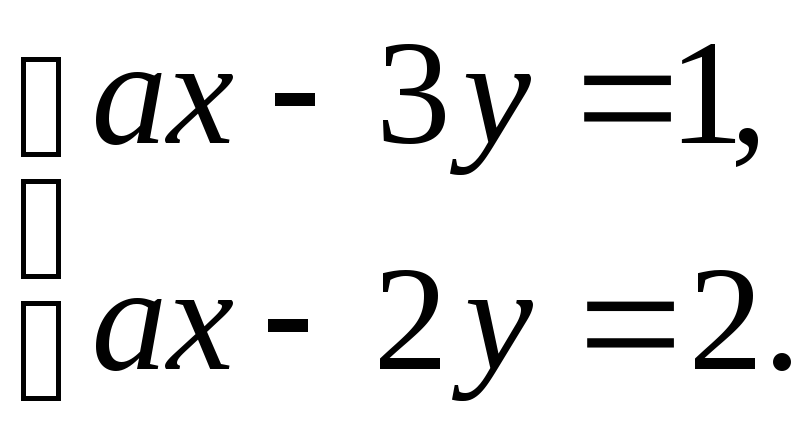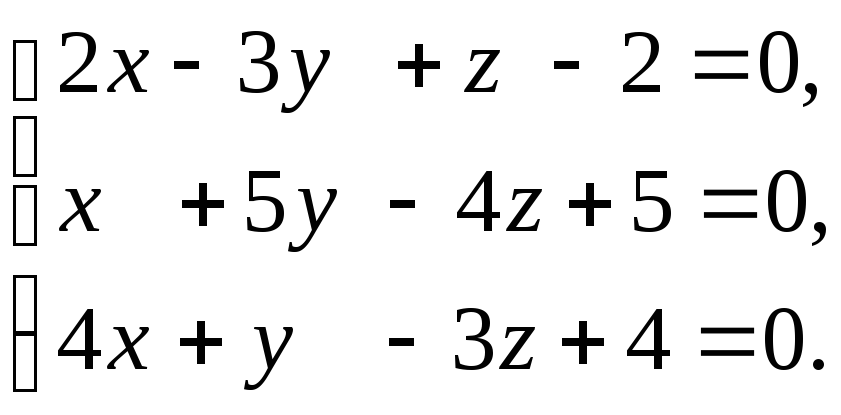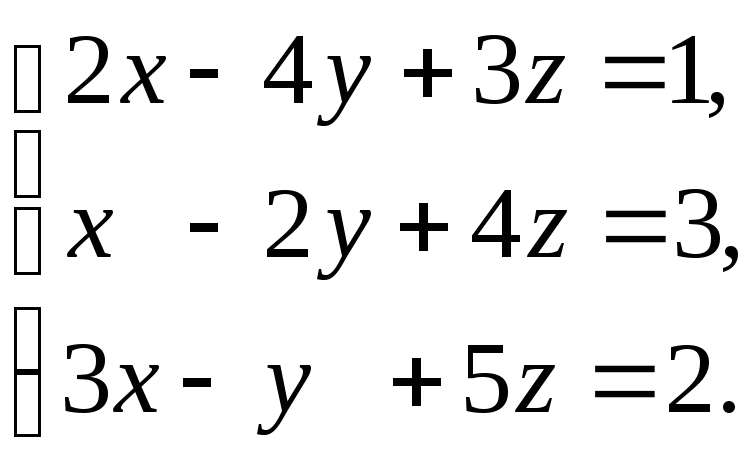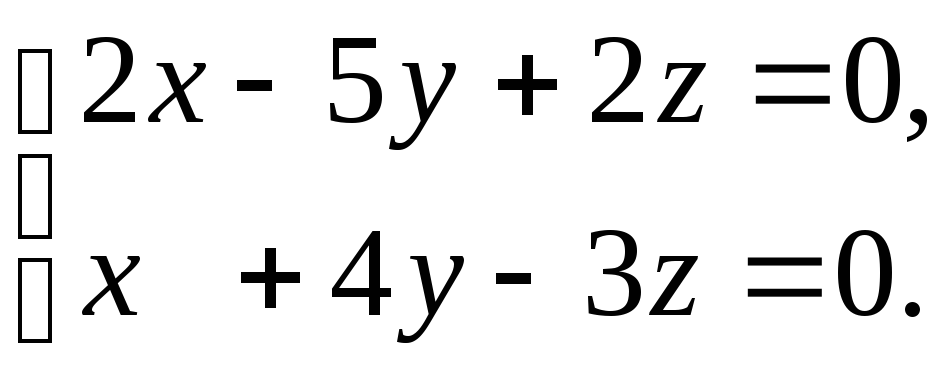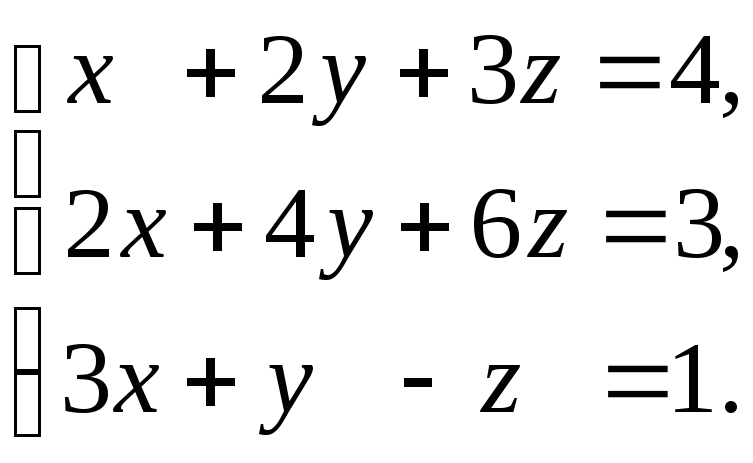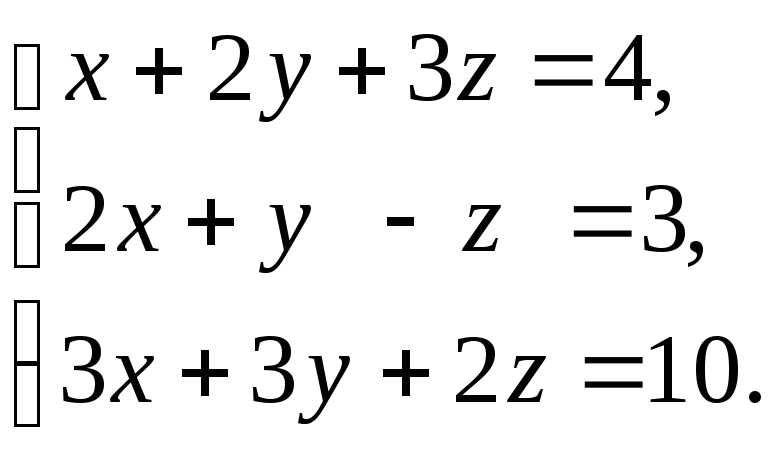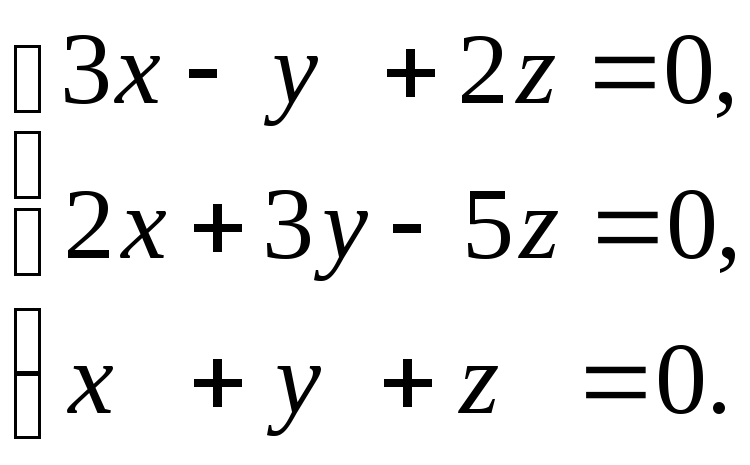Глава 1 элементы линейной алгебры

1. 1. Определители

Определителем второго порядка называется число, которое обозначается символом

и вычисляется по правилу

Числа называютсяэлементами определителя (первый индекс указывает номер строки, а второйномер столбца, на пересечении которых стоит этот элемент); диагональ, образованная элементами,, называетсяглавной, элементами ,побочной.

Аналогично вводится понятие определителя третьего порядка.

Определителем третьего порядка называется число, которое обозначается символом

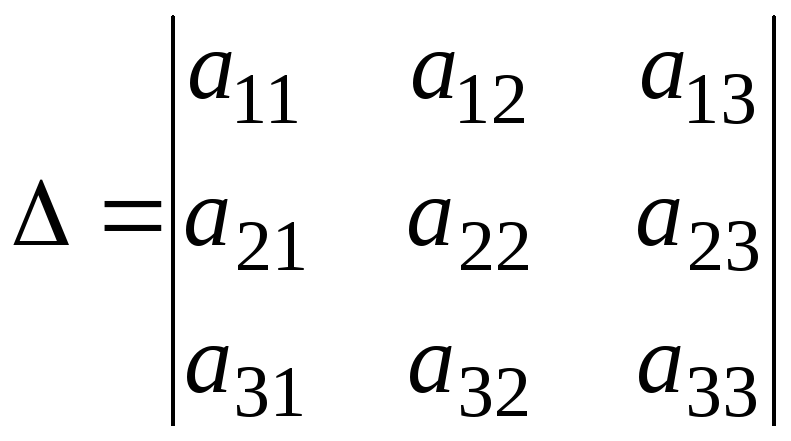
и вычисляется по правилу

Диагональ, образованная элементами ,,, называетсяглавной, элементами ,,побочной.

Чтобы запомнить какие произведения в правой части равенства (1) берутся со знаком «», а какие со знаком «», полезно использовать следующее «правило треугольников»:

Можно ввести понятие определителя 4-го, 5-го и т. д. порядков.

Минором некоторого элемента определителя называется определитель, образованный из данного вычёркиванием строки и столбца, на пересечении которых находится этот элемент.

Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на, гденомер строки,номер столбца, на пересечении которых находится этот элемент:

.

Свойства определителей.

1. Величина определителя не изменится, если его строки поменять местами со столбцами.

Рассмотренная операция называется транспонированием. Свойство 1

устанавливает равноправность строк и столбцов определителя.

2. Перестановка двух строк или двух столбцов определителя равносильна его умножению на .

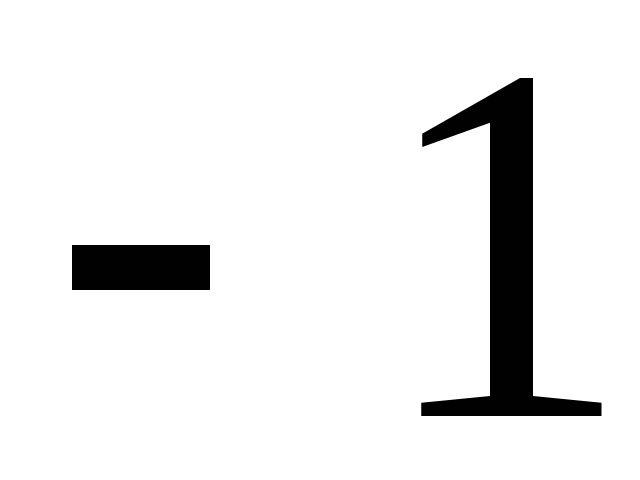3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то определитель равен нулю.

4. Постоянный множитель из строки или столбца можно выносить за знак определителя.

5. Если все элементы столбца или строки равны нулю, то и сам определитель равен нулю.

6. Если элементы двух столбцов или двух строк пропорциональны, то определитель равен нулю.

7. Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженные на любой общий множитель Я, то величина определителя не изменится.

8. Определитель равен сумме произведений элементов какого-либо столбца или строки на их алгебраические дополнения. Например,

.

Задачи для самостоятельного решения

Задача 1. Вычислить определители:

1) 2)3)4).

Задача 2. Вычислить определители, разложив их по элементам первого столбца:

1) 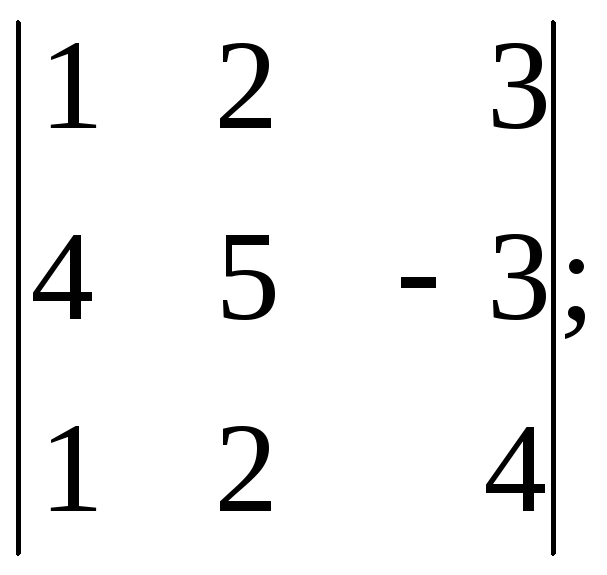2)

Задача 3. Найти из уравнений:

1) 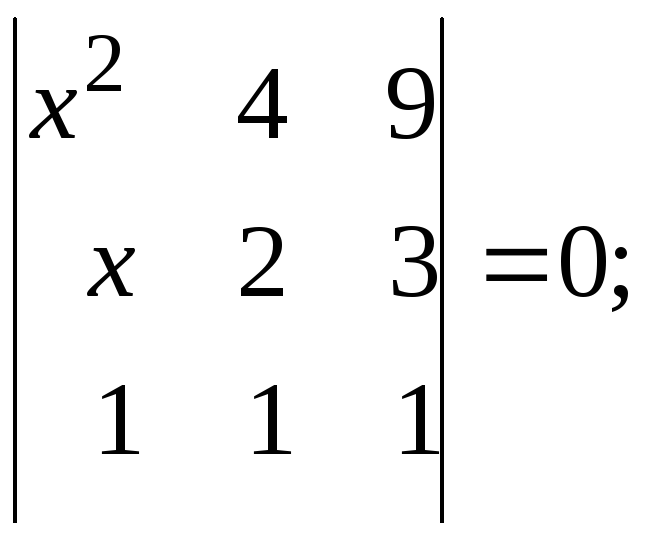2)

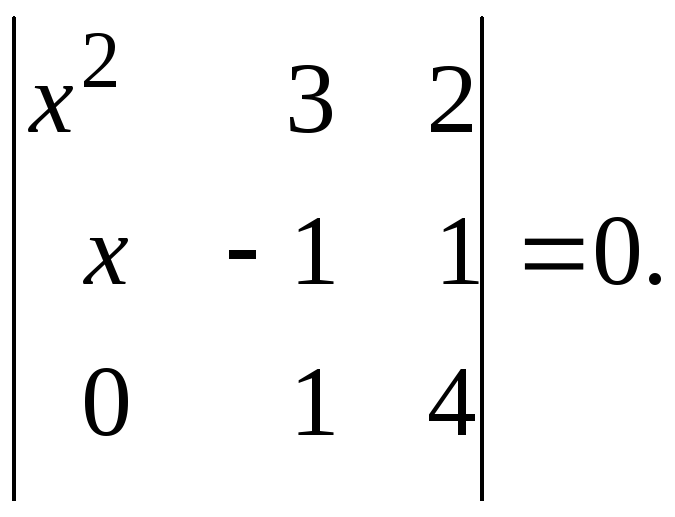
1.2. Решение систем линейных уравнений с помощью определителей. Формулы Крамера

I) Система двух линейных неоднородных уравнений с двумя неизвестными

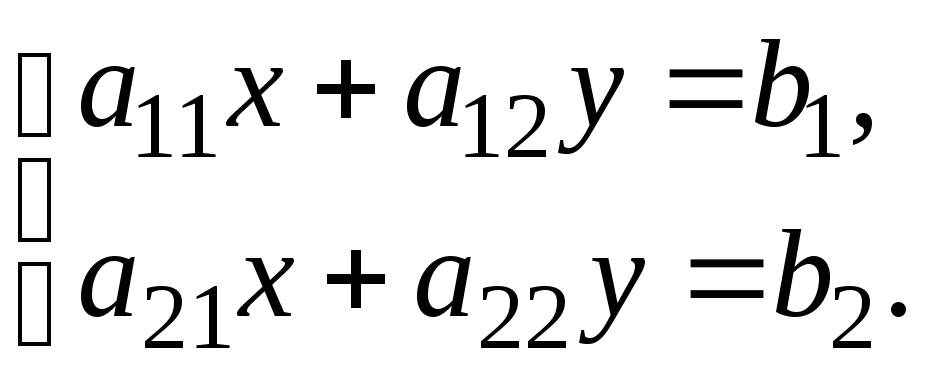
Обозначим

основной определитель системы;

, вспомогательные определители.

а) Если определитель системы , то система имеет единственное решение, которое находится по формулам Крамера:

, . (1)

б) Если определитель системы , то возможны случаи:

1) (уравнения пропорциональны), тогда система содержит только одно уравнение, например,и имеет бесконечно много решений (неопределённая система). Для её решения необходимо выразить одну переменную через другую, значение которой выбирается произвольно;

2) если хотя бы один из определителей отличен от нуля, то система не имеет решений (несовместная система).

II) Система двух линейных однородных уравнений с тремя переменными

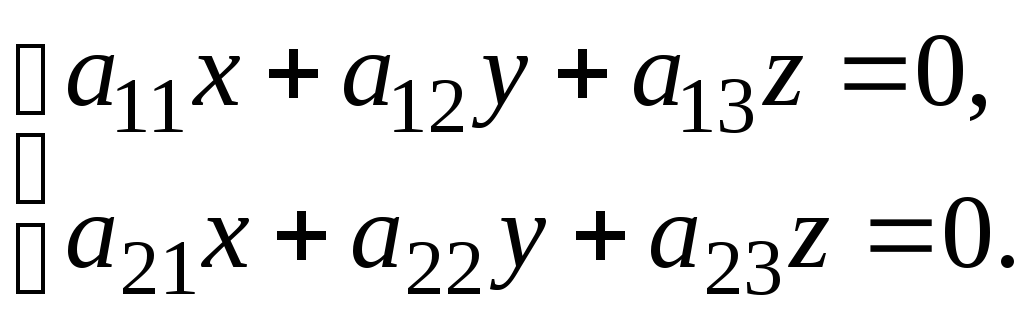(2)

Линейное уравнение называется однородным, если свободный член этого уравнения равен нулю.

а) Если , то система (2) сводится к одному уравнению (например, первому), из которого одно неизвестное выражается через два других, значения которых выбираются произвольно.

б) Если условие не выполнено, то для решения системы (2) перенесем одну переменную вправо и решим систему двух линейных неоднородных уравнений с использованием формул Крамера (1).

III) Система трёх линейных неоднородных уравнений с тремя неизвестными:

Составим и вычислим основной определитель и вспомогательные определители,.

а) Если , то система имеет единственное решение, которое находится по формулам Крамера:

, ,(3)

б) Если , то возможны случаи:

1) , тогда система будет иметь бесконечно много решений, она будет сводиться либо к системе состоящей из одного, либо из двух уравнений (одну неизвестную перенесём направо и решим систему двух уравнений с двумя неизвестными);

2) хотя бы один из определителей отличен от нуля, система не имеет решения.

IV) Система трёх линейных однородных уравнений с тремя неизвестными:

Эта система всегда совместна, так как имеет нулевое решение.

а) Если определитель системы , то она имеет единственное нулевое решение.

б) Если же , то система сводится либо к двум уравнениям (третье является их следствием), либо к одному уравнению (остальные два являются его следствием) и имеет бесконечно много решений (см. п.II).

Задача 4. Решить систему уравнений

Решение. Вычислим определитель системы

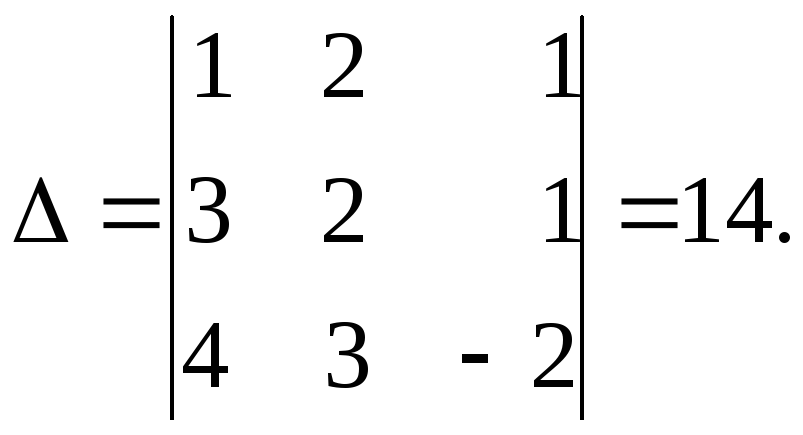
Так как , то система имеет единственное решение. Воспользуемся формулами Крамера (3). Для этого вычислим вспомогательные определители:

, ,

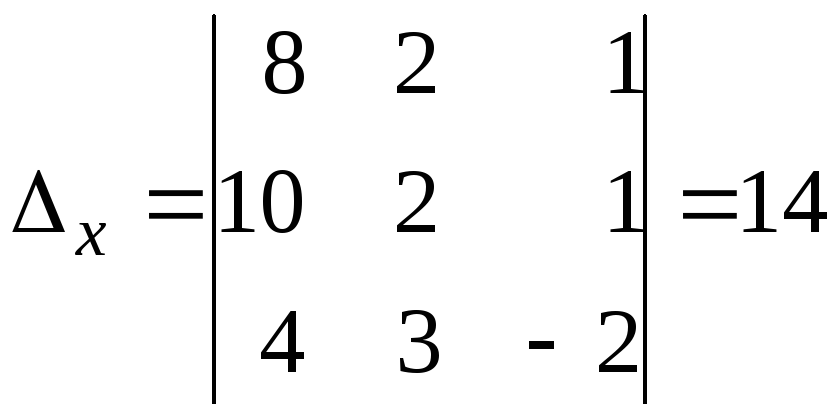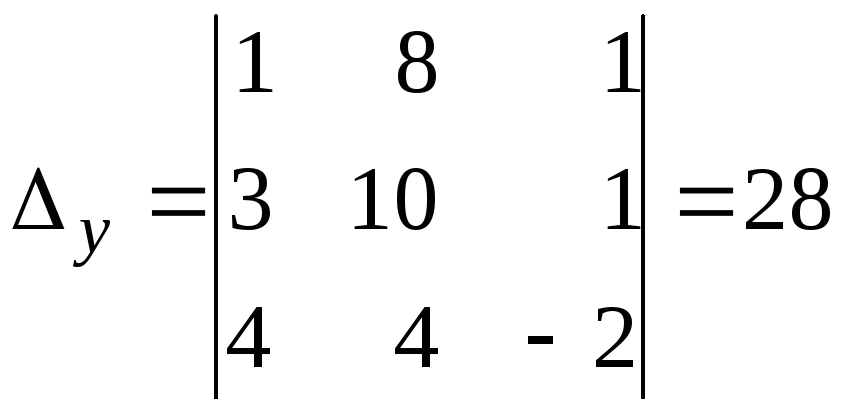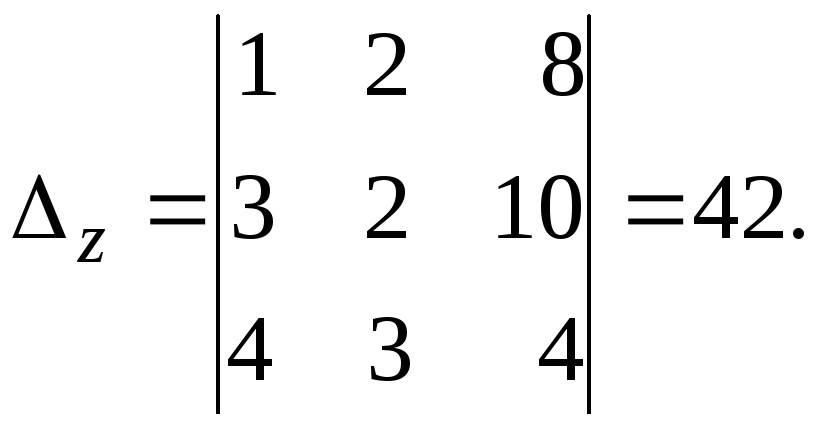
Тогда

, ,

Задача 5. Решить систему уравнений

Решение. Вычислим определитель системы:

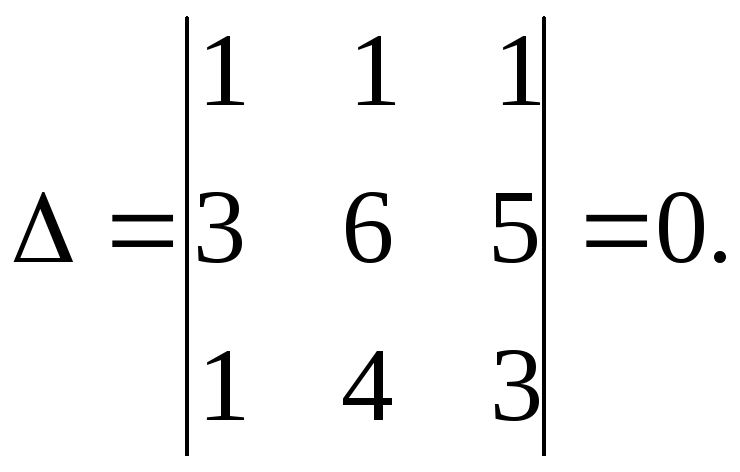
Следовательно, система однородных уравнений имеет бесконечно много решение, отличных от нулевого. Решаем систему первых двух уравнений (третье уравнение является их следствием):

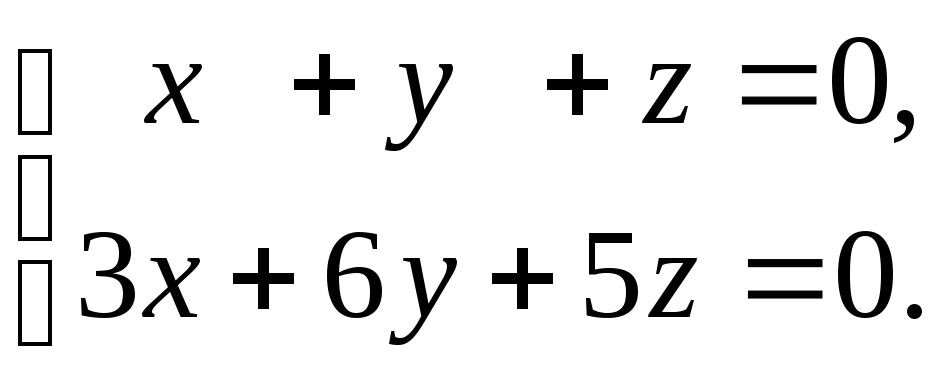
Перенесём переменную в правую часть равенства:

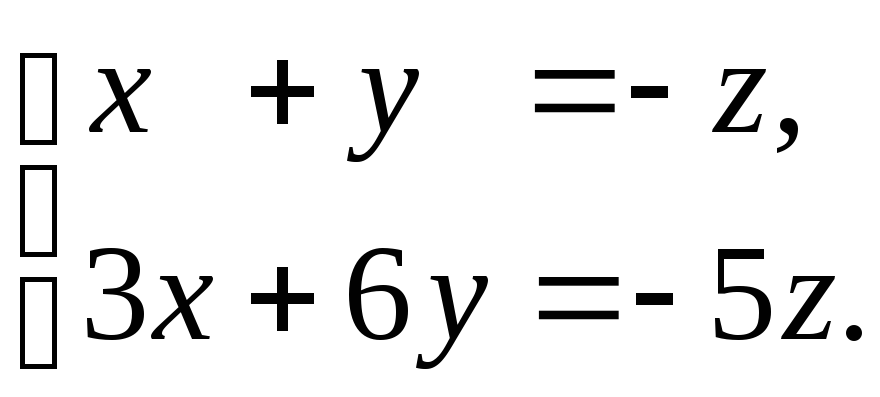
Отсюда по формулам (1) получаем

, .

Задачи для самостоятельного решения

Задача 6. Решить с помощью определителей системы уравнений:

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)